哈希的概念及其操作

哈希概念

順序結構以及平衡樹中，元素關鍵碼與其存儲位置之間沒有對應的關系，因此在查找一個元素時，必須要經過關鍵碼的多次比較。順序查找時間復雜度為O(N)，平衡樹中為樹的高度，即O( Log2N)，搜索的效率取決于搜索過程中元素的比較次數。
理想的搜索方法：可以不經過任何比較，一次直接從表中得到要搜索的元素。 如果構造一種存儲結構，通過某種函數(hashFunc)使元素的存儲位置與它的關鍵碼之間能夠建立一一映射的關系，那么在查找時通過該函數可以很快找到該元素。

當向該結構中：

  • 插入元素
    根據待插入元素的關鍵碼，以此函數計算出該元素的存儲位置并按此位置進行存放
  • 搜索元素
    對元素的關鍵碼進行同樣的計算，把求得的函數值當做元素的存儲位置，在結構中按此位置取元素比較，若關鍵碼相等，則搜索成功

該方式即為哈希(散列)方法，哈希方法中使用的轉換函數稱為哈希(散列)函數，構造出來的結構稱為哈希表(Hash Table)(或者稱散列表)
在這里插入圖片描述

哈希沖突

不同元素通過相同哈希函數計算出相同的哈希地址，該種現象稱為哈希沖突或哈希碰撞。
把具有不同關鍵碼而具有相同哈希地址的數據元素稱為“同義詞”。
在這里插入圖片描述
所以我們需要進一步的改進哈希函數來解決沖突

哈希函數

引起哈希沖突的一個原因可能是：哈希函數設計不夠合理。 哈希函數設計原則：

  • 哈希函數的定義域必須包括需要存儲的全部關鍵碼，而如果散列表允許有m個地址時，其值域必須在0到m-1之間
  • 哈希函數計算出來的地址能均勻分布在整個空間中
  • 哈希函數應該比較簡單

常用的哈希函數

  1. 直接定制法
    取關鍵字的某個線性函數為散列地址：Hash（Key）= A*Key + B 優點：簡單、均勻 缺點：需要事先知道關鍵字的分布情況 使用場景：適合查找比較小且連續的情況
  2. 除留余數法
    設散列表中允許的地址數為m，取一個不大于m，但最接近或者等于m的質數p作為除數，按照哈希函數：Hash(key) = key% p(p<=m),將關鍵碼轉換成哈希地址
  3. 平方取中法
    假設關鍵字為1234，對它平方就是1522756，抽取中間的3位227作為哈希地址； 再比如關鍵字為4321，對它平方就是18671041，抽取中間的3位671(或710)作為哈希地址 平方取中法比較適合：不知道關鍵字的分布，而位數又不是很大的情況
  4. 折疊法
    折疊法是將關鍵字從左到右分割成位數相等的幾部分(最后一部分位數可以短些)，然后將這幾部分疊加
    求和，并按散列表表長，取后幾位作為散列地址。折疊法適合事先不需要知道關鍵字的分布，適合關鍵字位數比較多的情況
  5. 隨機數法
    選擇一個隨機函數，取關鍵字的隨機函數值為它的哈希地址，即H(key) = random(key),其中random為隨機數函數。通常應用于關鍵字長度不等時采用此法
  6. 數學分析法
    假設要存儲某家公司員工登記表，如果用手機號作為關鍵字，那么極有可能前7位都是 相同的，那么我們可以選擇后面的四位作為散列地址，如果這樣的抽取工作還容易出現 沖突，還可以對抽取出來的數字進行反轉(如1234改成4321)、右環位移(如1234改成4123)、左環移位、前兩數與后兩數疊加(如1234改成12+34=46)等方法。數字分析法通常適合處理關鍵字位數比較大的情況，如果事先知道關鍵字的分布且關鍵字的若干位分布較均勻的情況
不論函數設計的多好----都不可能完全的解決哈希沖突

哈希函數的沖突解決

閉散列

也叫開放定址法，當發生哈希沖突時，如果哈希表未被裝滿，說明在哈希表中必然還有空位置，那
么可以把key存放到沖突位置中的“下一個” 空位置中去

1. 線性探測

  • 插入
    通過哈希函數獲取待插入元素在哈希表中的位置如果該位置中沒有元素則直接插入新元素，如果該位置中有元素發生哈希沖突，使用線性探測找到下一個空位置，插入新元素

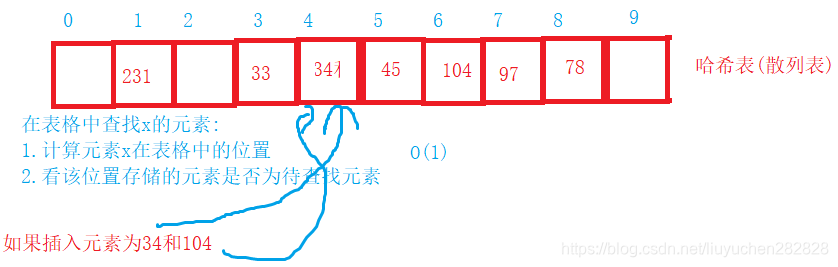
在這里插入圖片描述

  • 刪除
    采用閉散列處理哈希沖突時，不能隨便物理刪除哈希表中已有的元素，若直接刪除元素會影響其他元素的搜索。比如刪除元素34，如果直接刪除掉，104查找起來可能會受影響。因此線性探測采用標記的偽刪除法來刪除一個元素。
    在這里插入圖片描述

/ 哈希表每個空間給個標記
// EMPTY此位置空， EXIST此位置已經有元素， DELETE元素已經刪除
enum State{EMPTY, EXIST, DELETE};

線性探測實現

規定:表格中元素唯一
線性探測:表格中的元素一定不會存滿-----隨著元素不斷增多，產生哈希沖突的概率就急劇增加

#include<iostream>
using namespace std;
#include<vector>
enum State{ EMPTY, EXIST, DELETE };
template<class T>
class hashtable
{struct Elem  //存儲的元素類型{	Elem():_state(EMPTY){}T _data;State _state;};
public:hashtable(size_t capacity):_table(capacity), _size(0){}bool Insert(const T&data){//檢測哈希空間是否充足_CheckCapacity();//1.通過哈希函數計算哈希地址size_t hashAddr = HashFunc(data);//2.檢測位置是否可以存儲while(_table[hashAddr]._state != EMPTY){//檢測該位置元素是否有效&&是否為待插入元素if (EXIST == _table[hashAddr]._state&&data == _table[hashAddr]._data){return false;//元素已經存在，不進行插入}//發生哈希沖突++hashAddr;if (hashAddr == _table.capacity())//如果地址越界了，把地址放回0hashAddr = 0;}//3.插入元素_table[hashAddr]._data = data;_table[hashAddr]._state = EXIST;_size++;return true;}int Find(const T&data){size_t hashAddr = HashFunc(data);while (_table[hashAddr]._state != EMPTY){if (EXIST == _table[hashAddr]._state&&data == _table[hashAddr]._data){return hashAddr;}//發生哈希沖突hashAddr++;if (hashAddr == _table.capacity())hashAddr = 0;}return -1;}bool Erase(const T&data){int ret = Find(data);if (-1 != ret){_table[ret]._state = DELETE;--_size;return true;}return false;}size_t Size()const{return _size;}
private:size_t HashFunc(const T&data){return data%_table.capacity();}
private:vector<Elem>_table; //狀態表格size_t _size;
};

哈希算法

什么時候增容？

哈希的負載因子

哈希負載因子= 有效元素個數/哈希表的容量
哈希因子越小：產生沖突的概率越低
負載因子控制在0.7左右，性能就還可以
負載因子達到0.7，就需要進行擴容

擴容

void Swap(hashtable<T>& ht){_table.swap(ht._table);swap(_size, ht._size);swap(_total, ht._total);}
//擴容
void  _CheckCapacity()
{if (_total * 10 / _table.capacity() >= 7){//新的哈希表hashtable<T>newHT(_table.capacity() * 2);//獎舊哈希表中有效元素搬移到新的哈希表中//注意:已經刪除的元素不用搬移for (size_t i = 0; i < _table.capacity(); ++i){if (_table[i]._data == EXIST)newHT.Insert(_table[i]._data);}Swap(newHT);}
}

線性探測缺陷

容易產生數據的堆積-----產生沖突的元素全部集中在一起，一但產生沖突，可能會引起一連串的沖突，解決方法:二次探測

二次探測

線性探測的缺陷是產生沖突的數據堆積在一塊，這與其找下一個空位置有關系，因為找空位置的方式就是挨著往后逐個去找，因此二次探測為了避免該問題，找下一個空位置的方法為：H(i) = ( H(0)+i2 )% m,或者：H(i) = (H(0) -i2 )% m。其中：i = 1,2,3…， 是通過散列函數Hash(x)對元素的關鍵碼 key 進行計算得到的位置，m是表的大小。(i代表第幾次探測)

代碼實現

enum State{ EMPTY, EXIST, DELETE };
template<class T, bool IsLine = true>
class hashtable
{struct Elem  //存儲的元素類型{	Elem():_state(EMPTY){}T _data;State _state;};
public:hashtable(size_t capacity):_table(capacity), _size(0),_total(0){}bool Insert(const T&data){//檢測哈希空間是否充足_CheckCapacity();//1.通過哈希函數計算哈希地址size_t hashAddr = HashFunc(data);size_t i = 0;//二次探測中的第幾次探測//2.檢測位置是否可以存儲while(_table[hashAddr]._state != EMPTY){//檢測該位置元素是否有效&&是否為待插入元素if (EXIST == _table[hashAddr]._state&&data == _table[hashAddr]._data){return false;//元素已經存在，不進行插入}//發生哈希沖突if (IsLine){DetectiveLine(hashAddr);}else{++i;DetectiveTwice(hashAddr,i);}}//3.插入元素_table[hashAddr]._data = data;_table[hashAddr]._state = EXIST;_size++;_total++;return true;}int Find(const T&data){size_t hashAddr = HashFunc(data);size_t i = 0;while (_table[hashAddr]._state != EMPTY){if (EXIST == _table[hashAddr]._state&&data == _table[hashAddr]._data){return hashAddr;}//發生哈希沖突if (IsLine){DetectiveLine(hashAddr);}else{++i;DetectiveTwice(hashAddr,i);}}return -1;}bool Erase(const T&data){int ret = Find(data);if (-1 != ret){_table[ret]._state = DELETE;--_size;return true;}return false;}size_t Size()const{return _size;}void Swap(hashtable<T,IsLine>& ht){_table.swap(ht._table);swap(_size, ht._size);swap(_total, ht._total);}
private:size_t HashFunc(const T&data){return data%_table.capacity();}//線性探測void DetectiveLine(size_t&hashAddr){hashAddr += 1;if (hashAddr == _table.capacity())hashAddr = 0;}//二次探測void DetectiveTwice(size_t& hashAddr, size_t i){hashAddr = hashAddr + 2 * i + 1;if (hashAddr >= _table.capacity())hashAddr %= _table.capacity();}//擴容void  _CheckCapacity(){if (_total * 10 / _table.capacity() >= 7){//新的哈希表hashtable<T,IsLine>newHT(_table.capacity() * 2);//獎舊哈希表中有效元素搬移到新的哈希表中//注意:已經刪除的元素不用搬移for (size_t i = 0; i < _table.capacity(); ++i){if (_table[i]._data == EXIST)newHT.Insert(_table[i]._data);}Swap(newHT);}}
private:vector<Elem>_table; //狀態表格size_t _size;	//哈希表中有效元素的個數size_t _total; //哈希表中元素的個數:存在和刪除(為了保證哈希表中數據的唯一性，刪除位置不能插入元素)
};

研究表明：當表的長度為質數且表裝載因子a不超過0.5時，新的表項一定能夠插入，而且任何一個位置都不會被探查兩次。因此只要表中有一半的空位置，就不會存在表滿的問題。在搜索時可以不考慮表裝滿的情況，但在插入時必須確保表的裝載因子a不超過0.5，如果超出必須考慮增容

閉散列最大的缺陷就是空間利用率比較低，這也是哈希的缺陷。

開散列

開散列概念

開散列法又叫鏈地址法(開鏈法)，首先對關鍵碼集合用散列函數計算散列地址，具有相同地址的關鍵碼
歸于同一子集合，每一個子集合稱為一個桶，各個桶中的元素通過一個單鏈表鏈接起來，各鏈表的頭結點存儲在哈希表中。每個鏈表中保存發生哈希沖突的元素

代碼實現

//開散列:一個鏈表的集合---產生相同哈希地址的元素放到同一個鏈表里
#include<vector>
//哈希表的結點
template<class T>
struct HashNode
{HashNode(const T&data = T()):_pNext(nullptr), _data(data){}HashNode<T>* _pNext;T _data;
};template<class T>
class hashbucket
{typedef HashNode<T> Node;
public:hashbucket(size_t capacity):_table(capacity), _size(0){}~hashbucket(){Clear();}bool Insert(const T& data){//擴容_CheckCapacity();//通過哈希函數計算哈希的桶號size_t bucketNo = HashFunc(data);Node* pCur = _table[bucketNo];while (pCur){if (data == pCur->_data)return false;pCur = pCur->_pNext;}pCur = new Node(data);pCur->_pNext = _table[bucketNo];_table[bucketNo] = pCur;_size++;return true;}bool Erase(const T&data){//先找在哪個鏈表size_t bucketNo = HashFunc(data);//在鏈表中找元素Node* pCur = _table[bucketNo];Node* pPrev = nullptr;while (pCur){if (data == pCur->_data){//可以刪除if (pCur == _table[bucketNo])_table[bucketNo] = pCur->_pNext;elsepPrev->_pNext = pCur->_pNext;delete pCur;--_size;return true;}else{pPrev = pCur;pCur = pCur->_pNext;}}return false;}Node* Find(const T& data){size_t bucketNo = HashFunc(data);Node* pCur = _table[bucketNo];while (pCur){if (pCur->_data == data)return pCur;pCur = pCur->_pNext;}return nullptr;}size_t Size()const{return _size;}bool Empty()const{return 0 == _size;}void Clear(){for (size_t bucketNo = 0; bucketNo < _table.capacity(); ++bucketNo){Node* pCur = _table[bucketNo];while (pCur){_table[bucketNo] = pCur->_pNext;delete pCur;pCur = _table[bucketNo];}}}/*void _CheckCapacity(){if (_size == _table.capacity())}*///打印函數void PrintHashBucket(){for (int i = 0; i < _table.capacity(); ++i){Node* pCur = _table[i];cout << "table[" << i << "]:";while (pCur){cout << pCur->_data << "-->";pCur = pCur->_pNext;}cout << "NULL" << endl;}}
private:size_t HashFunc(const T&data){//T:可以是任意類型---可能不是整型return data % _table.capacity();}
private:vector<Node*> _table;//每一個鏈表的首地址size_t _size;  //當前哈希桶里放了多少個元素
};

開散列的增容

在這里插入圖片描述
桶的個數是一定的，隨著元素的不斷插入，每個桶中元素的個數不斷增多，極端情況下，可能會導致一個桶中鏈表節點非常多，會影響的哈希表的性能，因此在一定條件下需要對哈希表進行增容，那該條件怎么確認呢？開散列最好的情況是：每個哈希桶中剛好掛一個節點，再繼續插入元素時，每一次都會發生哈希沖突，因此，在元素個數剛好等于桶的個數時，可以給哈希表增容。
將舊哈希桶里的結點直接向新哈希桶里進行搬移，在新哈希桶里不要創建新的結點

void Swap(hashbucket<T>& ht)
{_table.swap(ht._table);swap(_size, ht._size);
}
void _CheckCapacity()
{if (_size == _table.capacity()){//新的哈希桶hashbucket<T> newHT(_table.capacity() * 2);//將舊哈希桶中的結點往新哈希桶中進行搬移for (size_t i = 0; i < _table.capacity(); ++i){Node* pCur = _table[i];//將i號桶中的所有結點搬移到新哈希桶中while (pCur){//將pCur結點從table的i號移除掉_table[i] = pCur->_pNext;//將pCur插入到新哈希桶中size_t bucketNo = newHT.HashFunc(pCur->_data);//采用頭插法pCur->_pNext = newHT._table[bucketNo];newHT._table[bucketNo] = pCur;newHT._size++;_size--;pCur = _table[i];}}//新桶和舊桶進行交換this->Swap(newHT);}
}

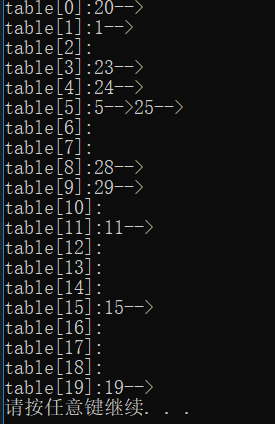
在這里插入圖片描述

哈希表只能存儲int類型的元素，如何實現任意類型

template<class T>
struct HashNode
{HashNode(const T&data = T()):_pNext(nullptr), _data(data){}HashNode<T>* _pNext;T _data;
};template<class T>
struct DefD2INIT
{const T& operator()(const T& data){return data;}
};struct Str2INT
{size_t operator()(const string& s){stringstream ss;ss << s;size_t ret;ss >> ret;return ret;}
};
template<class T,class DTOINT = DefD2INIT<T>>
class hashbucket
{typedef HashNode<T> Node;typedef hashbucket<T, DTOINT> Self;
public:hashbucket(size_t capacity):_table(capacity), _size(0){}~hashbucket(){Clear();}bool Insert(const T& data){//擴容_CheckCapacity();//通過哈希函數計算哈希的桶號size_t bucketNo = HashFunc(data);Node* pCur = _table[bucketNo];while (pCur){if (data == pCur->_data)return false;pCur = pCur->_pNext;}pCur = new Node(data);pCur->_pNext = _table[bucketNo];_table[bucketNo] = pCur;_size++;return true;}bool Erase(const T&data){//先找在哪個鏈表size_t bucketNo = HashFunc(data);//在鏈表中找元素Node* pCur = _table[bucketNo];Node* pPrev = nullptr;while (pCur){if (data == pCur->_data){//可以刪除if (pCur == _table[bucketNo])_table[bucketNo] = pCur->_pNext;elsepPrev->_pNext = pCur->_pNext;delete pCur;--_size;return true;}else{pPrev = pCur;pCur = pCur->_pNext;}}return false;}Node* Find(const T& data){size_t bucketNo = HashFunc(data);Node* pCur = _table[bucketNo];while (pCur){if (pCur->_data == data)return pCur;pCur = pCur->_pNext;}return nullptr;}size_t Size()const{return _size;}bool Empty()const{return 0 == _size;}void Clear(){for (size_t bucketNo = 0; bucketNo < _table.capacity(); ++bucketNo){Node* pCur = _table[bucketNo];while (pCur){_table[bucketNo] = pCur->_pNext;delete pCur;pCur = _table[bucketNo];}}}void Swap( Self& ht){_table.swap(ht._table);swap(_size, ht._size);}void _CheckCapacity(){if (_size == _table.capacity()){//新的哈希桶Self newHT(_table.capacity() * 2);//將舊哈希桶中的結點往新哈希桶中進行搬移for (size_t i = 0; i < _table.capacity(); ++i){Node* pCur = _table[i];//將i號桶中的所有結點搬移到新哈希桶中while (pCur){//將pCur結點從table的i號移除掉_table[i] = pCur->_pNext;//將pCur插入到新哈希桶中size_t bucketNo = newHT.HashFunc(pCur->_data);//采用頭插法pCur->_pNext = newHT._table[bucketNo];newHT._table[bucketNo] = pCur;newHT._size++;_size--;pCur = _table[i];}}//新桶和舊桶進行交換this->Swap(newHT);}}void PrintHashBucket(){for (int i = 0; i < _table.capacity(); ++i){Node* pCur = _table[i];cout << "table[" << i << "]:";while (pCur){cout << pCur->_data << "-->";pCur = pCur->_pNext;}cout << "NULL" << endl;}}
private:size_t HashFunc(const T&data){//T:可以是任意類型---可能不是整型return DTOINT ()(data) % _table.capacity();}
private:vector<Node*> _table;//每一個鏈表的首地址size_t _size;  //當前哈希桶里放了多少個元素
};

除留余數法，最好模一個素數，如何每次快速取一個類似兩倍關系的素數？

//素數表，以遞進兩倍方式給出
const int PRIMECOUNT = 28;
const size_t primeList[PRIMECOUNT] =
{53ul, 97ul, 193ul, 389ul, 769ul,1543ul, 3079ul, 6151ul, 12289ul, 24593ul,49157ul, 98317ul, 196613ul, 393241ul, 786433ul,1572869ul, 3145739ul, 6291469ul, 12582917ul, 25165843ul,50331653ul, 100663319ul, 201326611ul, 402653189ul, 805306457ul,1610612741ul, 3221225473ul, 4294967291ul
};size_t GetNextPrime(size_t prime)
{size_t i = 0;for (; i < PRIMECOUNT; ++i){//當前素數大于提供的素數if (primeList[i] > prime)//返回return primeList[i];}//返回最后一個return primeList[PRIMECOUNT - 1];
}

開散列與閉散列比較

應用鏈地址法處理溢出，需要增設鏈接指針，似乎增加了存儲開銷。事實上： 由于開地址法必須保持大量的空閑空間以確保搜索效率，如二次探查法要求裝載因子a <= 0.7，而表項所占空間又比指針大的多，所以使用鏈地址法反而比開地址法節省存儲空間。

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/383118.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/383118.shtml
英文地址，請注明出處：http://en.pswp.cn/news/383118.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

軟件工程---1.概述

軟件工程---1.概述

軟件的特征 抽象&#xff1a; 不可觸摸&#xff0c;邏輯實體&#xff0c;可記錄&#xff0c;但看不到復制成本低&#xff1a;不受物質材料的限制&#xff0c;不受物理定律或加工過程的制約&#xff0c;與開發成本相比&#xff0c;復制成本很低無折舊、受硬件制約、未完全擺脫手…
閱讀更多...
軟件工程---2.軟件過程

軟件工程---2.軟件過程

三個模型 瀑布模型增量模型集成和配置模型 沒有適用于所有不同類型軟件開發的過程模型。 瀑布模型 需求定義系統和軟件的設計實現與單元測試集成與系統測試運行與維護 瀑布模型的特征 從上一項活動中接受該項活動的工作成果&#xff08;工作產品&#xff09;&#xff0c;作…
閱讀更多...
軟件工程---3.敏捷軟件開發

軟件工程---3.敏捷軟件開發

敏捷軟件開發 極限編程&#xff08;XP&#xff0c; Beck1999&#xff09;Scrum方法&#xff08;Schwaber and Beedle 2001&#xff09;DSDM方法&#xff08;Stapleton 2003&#xff09; 敏捷軟件的開發宣言 個體和交互勝過過程和工具可以工作的軟件勝過面面俱到的文檔客戶合…
閱讀更多...
軟件工程---4.需求工程

軟件工程---4.需求工程

需求工程定義 找出、分析、文檔化并且檢查需求的過程被稱為需求工程 需求的兩個描述層次 用戶需求&#xff0c;指高層的抽象需求。使用自然語言、圖形描述需求。系統需求&#xff0c;指底層的詳細需求。使用系統需求文檔&#xff08;有時被稱為功能規格說明&#xff09;應該…
閱讀更多...
軟件工程---5.系統建模

軟件工程---5.系統建模

從不同視角對系統建模 外部視角&#xff0c;上下文模型&#xff0c;對系統上下文或環境建模交互視角&#xff0c;交互模型&#xff08;功能模型&#xff09;&#xff0c;對系統與參與者或系統內構件之間的交互建模結構視角&#xff0c;結構模型&#xff08;靜態模型&#xff0…
閱讀更多...
軟件工程---6.體系結構設計

軟件工程---6.體系結構設計

體系結構模型是什么&#xff1f; 體系結構模型&#xff0c;該模型描述系統如何被組織為一組相互通信的構件 體系結構分類 小體系結構關注單個程序的體系結構。在這個層次上&#xff0c;我們關注單個的程序是如何補分解為構件的。大體系結構關注包括其他系統、程序和程序構件…
閱讀更多...
【劍指offer】_06 變態跳臺階

【劍指offer】_06 變態跳臺階

題目描述 一只青蛙一次可以跳上1級臺階&#xff0c;也可以跳上2級……它也可以跳上n級。求該青蛙跳上一個n級的臺階總共有多少種跳法。 解題思路 鏈接&#xff1a;https://www.nowcoder.com/questionTerminal/22243d016f6b47f2a6928b4313c85387 關于本題&#xff0c;前提是…
閱讀更多...
【劍指offer】_07 矩形覆蓋

【劍指offer】_07 矩形覆蓋

題目描述 我們可以用21的小矩形橫著或者豎著去覆蓋更大的矩形。請問用n個21的小矩形無重疊地覆蓋一個2*n的大矩形&#xff0c;總共有多少種方法&#xff1f; 解題思路 依舊是斐波那契數列 2n的大矩形&#xff0c;和n個21的小矩形 其中target*2為大矩陣的大小 有以下幾種情形…
閱讀更多...
軟件工程---07.設計與實現

軟件工程---07.設計與實現

軟件設計和軟件實現 軟件設計是一個創造性的活動&#xff0c;在此活動中需要基于客戶需求識別軟件構件及其關系。軟件實現是將設計實現為一個程序的過程 為開發一個系統設計&#xff0c;你需要 理解并定義上下文模型以及系統的外部交互設計系統體系結構識別系統中的主要對象…
閱讀更多...
軟件工程---08.軟件測試

軟件工程---08.軟件測試

測試 測試的正向思維&#xff08;確認測試&#xff09; 向開發人員和客戶展示軟件滿足其需求測試的逆向思維&#xff08;缺陷測試&#xff09;找出可能導致軟件行為不正確原因。測試是更廣闊的軟件確認和驗證( Verification and Validation; V & V)過程的一部分。驗證和確…
閱讀更多...
軟件工程---15.軟件復用

軟件工程---15.軟件復用

復用的圖(牢記) 軟件復用的好處 開發加速有效的專家利用提高可依賴性降低開發成本降低過程風險符合標準 軟件復用的缺點 創建&#xff0c;維護以及使用一個構件庫查找&#xff0c;理解以及適配可復用構件維護成本增加缺少工具支持“不是在這里發明的”綜合癥 應用框架 現在…
閱讀更多...
軟件工程---16.基于構件的軟件工程

軟件工程---16.基于構件的軟件工程

CBSE CBSE是定義、實現、集成或組裝松散耦合的獨立構件成為系統的過程。 基于構件的軟件工程的要素有: 完全由接口進行規格說明的獨立構件。構件標準使構件集成變得更為容易。中間件為構件集成提供軟件支持。開發過程適合基于構件的軟件工程。 CBSE的設計原則 構件是獨立的…
閱讀更多...
軟件工程---17.分布式軟件工程

軟件工程---17.分布式軟件工程

分布式系統的5個優點 資源共享開放性并發性可伸縮性容錯性 分布式計算中必須考慮的設計問題 透明性&#xff1a;隱藏底層分布 開放性 可伸縮性 三個維度 規模&#xff1a;又分為增強擴展(單挑)&#xff0c;增加擴展(群毆)分布可靠性 信息安全性 主要防止以下類型的攻擊 攔…
閱讀更多...
軟件工程---18.面向服務的軟件工程

軟件工程---18.面向服務的軟件工程

什么是Web服務 一個松耦合、可復用的軟件構件&#xff0c;封裝了離散的功能&#xff0c;該功能是分布式的并且可以被程序訪問。Web服務是通過標準互聯網和基于XML的協議被訪問的服務。 服務和軟件構件之間的一個重要的區別是 服務應該總是獨立的和松耦合的Web 服務沒有“請求…
閱讀更多...
【劍指offer】_08.數值的整數次方

【劍指offer】_08.數值的整數次方

題目描述 給定一個double類型的浮點數base和int類型的整數exponent。求base的exponent次方。 保證base和exponent不同時為0 解題思路 首先一個數的任意次方&#xff0c;這個數有可能是負數和正數和零&#xff0c;然后次方也有可能是負數和正數和零 當這個數是零時&#xff…
閱讀更多...
【劍指offer】_09二叉搜索樹的后序遍歷序列

【劍指offer】_09二叉搜索樹的后序遍歷序列

題目描述 輸入一個整數數組&#xff0c;判斷該數組是不是某二叉搜索樹的后序遍歷的結果。如果是則輸出Yes,否則輸出No。假設輸入的數組的任意兩個數字都互不相同。 解題思路 比如下面的這棵二叉搜索樹 它的后序遍歷為0214369875&#xff1b; 我們設當前根節點為root; 第一次…
閱讀更多...
【劍指offer】_10二叉樹和為某一路徑值

【劍指offer】_10二叉樹和為某一路徑值

題目描述 輸入一顆二叉樹的跟節點和一個整數&#xff0c;打印出二叉樹中結點值的和為輸入整數的所有路徑。路徑定義為從樹的根結點開始往下一直到葉結點所經過的結點形成一條路徑。 解題思路 要求一路徑的和&#xff0c;那么必然終止條件為葉子結點&#xff0c;從根結點出發…
閱讀更多...
【劍指offer】_11整數中1出現的次數

【劍指offer】_11整數中1出現的次數

題目描述 求出1~13的整數中1出現的次數,并算出100~1300的整數中1出現的次數&#xff1f;為此他特別數了一下1~13中包含1的數字有1、10、11、12、13因此共出現6次,但是對于后面問題他就沒轍了。ACMer希望你們幫幫他,并把問題更加普遍化,可以很快的求出任意非負整數區間中1出現的…
閱讀更多...
【劍指offer】_12 數組中的逆序對

【劍指offer】_12 數組中的逆序對

題目描述 在數組中的兩個數字&#xff0c;如果前面一個數字大于后面的數字&#xff0c;則這兩個數字組成一個逆序對。輸入一個數組,求出這個數組中的逆序對的總數P。并將P對1000000007取模的結果輸出。 即輸出P%1000000007 解題思路 劍指offer的解法 看到這個題目&#xff0…
閱讀更多...
詳解Linux下通過yum安裝Mariadb/MySQL數據庫(騰訊云也適用)

詳解Linux下通過yum安裝Mariadb/MySQL數據庫(騰訊云也適用)

1. 安裝Mariadb 安裝命令 yum -y install mariadb mariadb-server安裝完成MariaDB&#xff0c;首先啟動MariaDB systemctl start mariadb設置開機啟動 systemctl enable mariadbMariaDB的相關簡單配置 此命令進入到配置相關界面 mysql_secure_installation首先是設置密碼…
閱讀更多...
最新文章

Copyright @ 2022~2023