?劍指 Offer 11. 旋轉數組的最小數字

難度：簡單

把一個數組最開始的若干個元素搬到數組的末尾，我們稱之為數組的旋轉。

給你一個可能存在 重復 元素值的數組 numbers ，它原來是一個升序排列的數組，并按上述情形進行了一次旋轉。請返回旋轉數組的最小元素。例如，數組 [3,4,5,1,2] 為 [1,2,3,4,5] 的一次旋轉，該數組的最小值為 1。

注意，數組 [a[0], a[1], a[2], ..., a[n-1]] 旋轉一次 的結果為數組 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

示例 1：

輸入：numbers = [3,4,5,1,2]
輸出：1

示例 2：

輸入：numbers = [2,2,2,0,1]
輸出：0

提示：

• n == numbers.length
• 1 <= n <= 5000
• -5000 <= numbers[i] <= 5000
• numbers 原來是一個升序排序的數組，并進行了 1 至 n 次旋轉

注意：本題與 154. 尋找旋轉排序數組中的最小值 II 相同。

💡思路：二分查找

將旋轉數組對半分可以得到一個包含最小元素的新旋轉數組，以及一個非遞減排序的數組。新的旋轉數組的長度是原數組的一半，從而將問題規模減少了一半，這種折半性質的算法的時間復雜度為 $O(log2N)$。

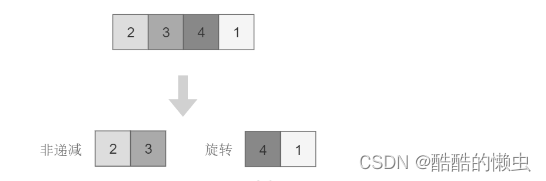
此時問題的關鍵在于確定對半分得到的兩個數組哪一個是旋轉數組，哪一個是非遞減數組。我們很容易知道非遞減數組的第一個元素一定小于等于最后一個元素。

通過修改二分查找算法進行求解（left、mid、right 分別代表包含最小元素的新旋轉數組 左、中、右）：

1. 當 numbers[mid] > numbers[right]時， [left，mid] 區間內的數組是非遞減數組，[mid + 1, right] 區間內的數組為新的旋轉數組，此時，left = mid + 1；
2. 當 numbers[mid] < numbers[right]時， [mid，right] 區間內的數組是非遞減數組，[left, mid] 區間內的數組為新的旋轉數組，此時，right = mid；
3. 當 numbers[mid] = numbers[right]時， 無法判斷哪一個是旋轉數組，哪一個是非遞減數組，此時 right- -，直到能判斷。

🍁代碼：(C++、Java)

C++

class Solution {
public:int minArray(vector<int>& numbers) {int left = 0;int right = numbers.size() - 1;if(right == 0) return numbers[0];while(left < right){int mid = left + (right - left) / 2;if(numbers[mid] > numbers[right]){left = mid + 1;}else if(numbers[mid] < numbers[right]){right = mid;}else{right--;}}return numbers[left];}
};

Java

class Solution {public int minArray(int[] numbers) {int left = 0;int right = numbers.length - 1;if(right == 0) return numbers[0];while(left < right){int mid = left + (right - left) / 2;if(numbers[mid] > numbers[right]){left = mid + 1;}else if(numbers[mid] < numbers[right]){right = mid;}else{right--;}}return numbers[left];}
}

🚀 運行結果：

🕔 復雜度分析：

• 時間復雜度：$O(logn)$，平均時間復雜度為 $O(log?n)$，其中 n 是數組 numbers 的長度。如果數組是隨機生成的，那么數組中包含相同元素的概率很低，在二分查找的過程中，大部分情況都會忽略一半的區間。而在最壞情況下，如果數組中的元素完全相同，那么 while 循環就需要執行 n 次，每次忽略區間的右端點，時間復雜度為 O(n)。
• 空間復雜度：$O(1)$。

題目來源：力扣。

放棄一件事很容易，每天能堅持一件事一定很酷，一起每日一題吧！
關注我LeetCode主頁 / CSDN—力扣專欄，每日更新！

注： 如有不足，歡迎指正！