文章轉載自：https://blog.csdn.net/zengxiantao1994/article/details/72787849
極大似然估計-形象解釋看這篇文章：https://www.zhihu.com/question/24124998
貝葉斯定理-形象解釋看這篇文章：https://www.zhihu.com/question/19725590/answer/217025594
極大似然估計
? ? ? ? 以前多次接觸過極大似然估計，但一直都不太明白到底什么原理，最近在看貝葉斯分類，對極大似然估計有了新的認識，總結如下：
貝葉斯決策
? ? ? ? 首先來看貝葉斯分類，我們都知道經典的貝葉斯公式：
?
? ? ? ? 其中：p(w)：為先驗概率，表示每種類別分布的概率；
? ? ? ? 我們來看一個直觀的例子：已知：在夏季，某公園男性穿涼鞋的概率為1/2，女性穿涼鞋的概率為2/3，并且該公園中男女比例通常為2:1，問題：若你在公園中隨機遇到一個穿涼鞋的人，請問他的性別為男性或女性的概率分別為多少？
? ? ? ? 從問題看，就是上面講的，某事發生了，它屬于某一類別的概率是多少？即后驗概率。
? ? ? ? 設：
? ? ? ? 由已知可得：
?
? ? ? ? 男性和女性穿涼鞋相互獨立，所以
（若只考慮分類問題，只需要比較后驗概率的大小，的取值并不重要）。
? ? ? ? 由貝葉斯公式算出：
???
問題引出
? ? ? ? 但是在實際問題中并不都是這樣幸運的，我們能獲得的數據可能只有有限數目的樣本數據，而先驗概率
? ? ? ? 先驗概率的估計較簡單，1、每個樣本所屬的自然狀態都是已知的（有監督學習）；2、依靠經驗；3、用訓練樣本中各類出現的頻率估計。
? ? ? ? 類條件概率的估計（非常難），原因包括：概率密度函數包含了一個隨機變量的全部信息；樣本數據可能不多；特征向量x的維度可能很大等等。總之要直接估計類條件概率的密度函數很難。解決的辦法就是，把估計完全未知的概率密度
重要前提
? ? ? ? 上面說到，參數估計問題只是實際問題求解過程中的一種簡化方法（由于直接估計類條件概率密度函數很困難）。所以能夠使用極大似然估計方法的樣本必須需要滿足一些前提假設。
? ? ? ??重要前提：訓練樣本的分布能代表樣本的真實分布。每個樣本集中的樣本都是所謂獨立同分布的隨機變量?(iid條件)，且有充分的訓練樣本。
極大似然估計
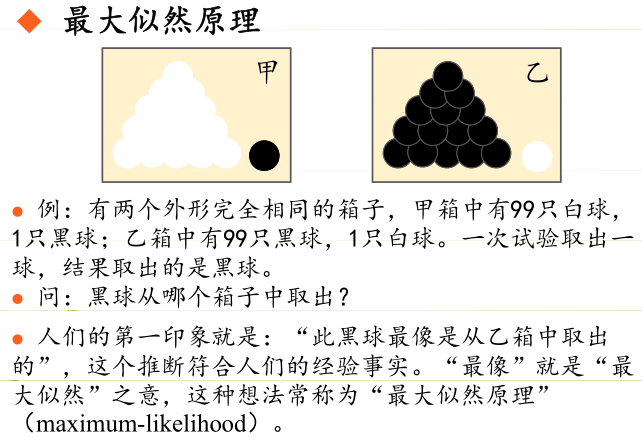
? ? ? ? 極大似然估計的原理，用一張圖片來說明，如下圖所示：
?
? ? ? ? 總結起來，最大似然估計的目的就是：利用已知的樣本結果，反推最有可能（最大概率）導致這樣結果的參數值。
? ? ? ? 原理：極大似然估計是建立在極大似然原理的基礎上的一個統計方法，是概率論在統計學中的應用。極大似然估計提供了一種給定觀察數據來評估模型參數的方法，即：“模型已定，參數未知”。通過若干次試驗，觀察其結果，利用試驗結果得到某個參數值能夠使樣本出現的概率為最大，則稱為極大似然估計。
? ? ? ? 由于樣本集中的樣本都是獨立同分布，可以只考慮一類樣本集D，來估計參數向量θ。記已知的樣本集為：
?? 似然函數（linkehood function）：聯合概率密度函數
?
? ? ? ? 如果
?
求解極大似然函數
? ? ? ? ML估計：求使得出現該組樣本的概率最大的θ值。
?
???????? 實際中為了便于分析，定義了對數似然函數：
??
? ? ? ? 1. 未知參數只有一個（θ為標量）
? ? ? ? 在似然函數滿足連續、可微的正則條件下，極大似然估計量是下面微分方程的解：
? ? ? ? 2.未知參數有多個（θ為向量）
? ? ? ? 則θ可表示為具有S個分量的未知向量：
?
???????? 記梯度算子：
?
???????? 若似然函數滿足連續可導的條件，則最大似然估計量就是如下方程的解。
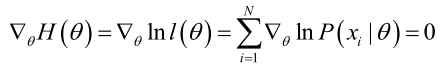
?????????方程的解只是一個估計值，只有在樣本數趨于無限多的時候，它才會接近于真實值。
極大似然估計的例子
? ? ? ? 例1：設樣本服從正態分布
?
? ? ? ? 它的對數：
?
? ? ? ? 求導，得方程組：
?
? ? ? ? 聯合解得：
?
? ? ? ? 似然方程有唯一解
?
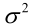
? ? ? ? 例2：設樣本服從均勻分布[a, b]。則X的概率密度函數：
?
? ? ? ? 對樣本
?
? ? ? ? 很顯然，L(a,b)作為a和b的二元函數是不連續的，這時不能用導數來求解。而必須從極大似然估計的定義出發，求L(a,b)的最大值，為使L(a,b)達到最大，b-a應該盡可能地小，但b又不能小于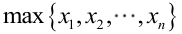
?
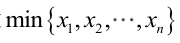
總結
? ? ? ? 求最大似然估計量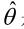
? ? ? ? （1）寫出似然函數；
? ? ? ? （2）對似然函數取對數，并整理；
? ? ? ? （3）求導數；
? ? ? ? （4）解似然方程。
? ? ? ? 最大似然估計的特點：
? ? ? ? 1.比其他估計方法更加簡單；
? ? ? ? 2.收斂性：無偏或者漸近無偏，當樣本數目增加時，收斂性質會更好；
? ? ? ? 3.如果假設的類條件概率模型正確，則通常能獲得較好的結果。但如果假設模型出現偏差，將導致非常差的估計結果。
?
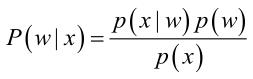
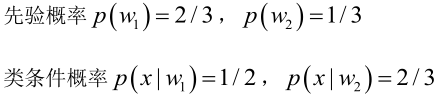
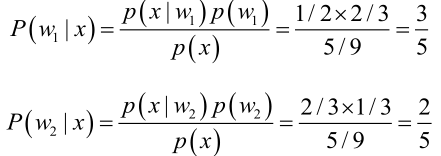
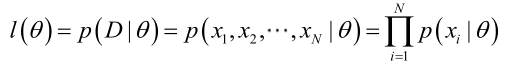
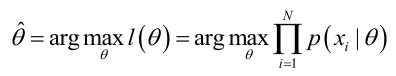
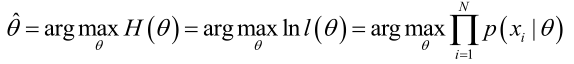
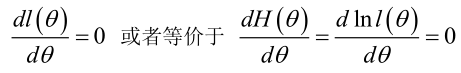
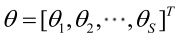
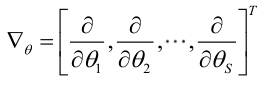
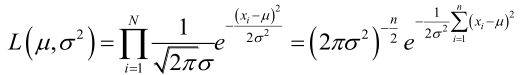
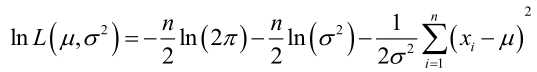
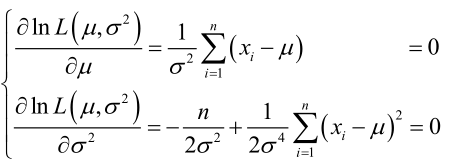
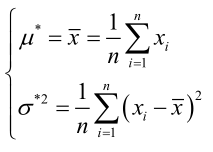
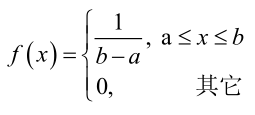
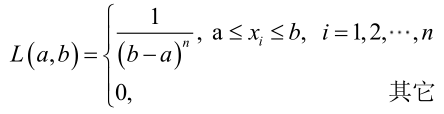
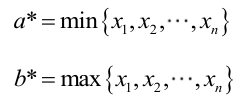
