首先，小編先給大家介紹一些關于組裝的歷史。大家肯定也知道，這個組裝技術的發展是依賴于測序技術的。首先在一代測序的時候，測序數據量較少，成本較高，人們對于組裝的結首先，小編先給大家介紹一些關于組裝的歷史。大家肯定也知道，這個組裝技術的發展是依賴于測果預期也比較低，弄到contig水平就可以啦，還有就是這個組裝的物種基因組都偏小。因此那個時候的組裝軟件都是基于overlap的。然后呢，二代測序技術來了，數據量超高，成本也便宜啦。科研工作者就想啊，現在都二代了，這個組裝的預期得提高啊，得與時俱進啊。但是基于overlap的組裝不了太長，而且超級慢，又加之，二代數據量太多，overlap扛不住啊。因此有人就開發出了基于圖論的組裝算法。然后呢，三代測序技術這兩年出來了，科學家一看，我x，這么長的read，那還搞毛圖論的算法，直接簡單粗暴點，用overlap多簡單，于是基于overlap的軟件又火了，去年一個三代基于圖論的軟件發表，將基于圖論的組裝再次放在了風口浪尖。

大家好，我是生信人小編XIXI，與青壬同學遙相呼應地，坐標魔都西南……平時做項目總會遇到一些很有意思的文章或者算法，或者一些很有用的工具，會有拍案叫絕的沖動(當然更多時候有想摔桌子的沖動)，所以呢希望能通過這個平臺和大家一起分享。

最近有在看一些關于從頭拼接(de novo)相關的文章。De novo的方法大部分是當基因組、轉錄組或者蛋白組信息缺失嚴重或者想要研究修飾的時候使用，它可以不用借助任何參考組直接進行推測拼接，但相對來說準確度會比較低一些。

其實不難發現，大部分de novo的文章都是基于圖論分析，比如大部分基因組和轉錄組de novo；蛋白組的質譜數據分析屬于“看圖說話”，以前的很多工具也是基于圖論，最近有出來很多基于機器學習的工具，運行速度也有大幅提升，如果大家感興趣后邊也可以給大家講講。

最近想使用SOAPdenovo-Trans來進行RNA-seq的de novo分析

所以對它的原理及運行過程進行了一下簡單摸索。在轉錄組方面，如果是測序比較完全的生物，大多數人是會選擇將測序的read直接匹配到參考基因組上邊的(還記得大明湖畔的Tophat和cufflinks么)；但是如果是一些參考基因組缺失的或者基因組非常龐大的物種，de novo的方法則可以很好地解決這個問題。

De Bruijn graph (DBG)可以說基本是大部分組裝方法的核心所在，有很大一部分的轉錄組拼接軟件(Oases，SOAPdenovo-Trans等)都是依賴于這個算法的。這里給大家做一個比較通俗的介紹。

比如我們手上有真實的RNA序列AUCGAAUCCCGAA，通過 RNA-seq可以得到的6條read：

那怎么從這6個小片段推導出它真實的序列信息呢？(如果你一眼看出來了，請原諒我寬容地排列整齊……)

首先，假如我們設定K-mers為3-mers，也就是說我們可以將所有的read都切割3個堿基長度的子序列，如下：

接著，我們可以將每個子序列都可以看成一個結點，每個read中的子序列結點可以依次用箭頭連接，依次建立這樣一張有向圖：

最后一張即為最終的de Bruijn graph (DBG)。那么怎么通過這張圖得到相應的序列呢？

學過圖論的旁友們大概可以會心一笑，那就是解歐拉路徑(Eulerian Tour)！也就是在最后這張圖里使得每條路徑被經過且僅經過一次。這個例子里可以很簡單的可以看出來(真實的案例里大約看的出來算我輸……)：

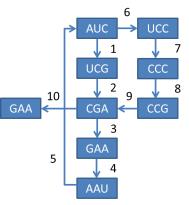
串起來就可以得到：AUCGAAUCCCGAA，也就是我們最開始的RNA序列了！具體解歐拉途徑的算法圖論中應該會有比較多的討論，有興趣的大神可以親手實現一下。

在該算法中K的選擇是有一定講究的，一般來說K小于等于最短read的長度，如果太短拼接效果又會比較差。SOAPdenovo-Trans中一般會設定~35作為K值。

De Bruijn graph的組裝方法相對時間復雜度比較低，為O(min(N,G))，G=genome length，N= total length of reads，與重疊方法的拼接過程相比可以大大節約時間成本；但它存在的問題是很可能你得到的路徑和你輸入的read是不匹配的，另外對于重復序列的處理也不是很棒。

更多套路，生信分析需求，請加微信：13895744602

歡迎關注生信人

TCGA | 小工具 | 數據庫 |組裝| 注釋 | 基因家族 | Pvalue

基因預測 |bestorf | sci | NAR | 在線工具 | 生存分析 | 熱圖

生信不死 | 初學者 | circRNA | 一箭畫心| 十二生肖 | circos

舞臺|基因組 | 黃金測序 | 套路 | 雜談組裝 | 進化 | 測序簡史