目錄

一、沒有免費的午餐定理

二、支持向量機SVM（support vector machine）

1、線性模型和非線性模型

2、如何在線性模型中畫出一條直線（優化過程——vplink）

1）多少條？

2）如何畫出最好的直線？

3、如何去描述這個優化的過程（數學描述）

1）幾個重要的名詞（間隔、支持向量）

2）一些定義（訓練數據、標簽、超平面等）

>>>問題1：怎么求解w,b？

3）機器學習的任務與步驟（求解w,b）

三、支持向量機的優化問題（求最優劃分直線，性能指標為d）

1、優化問題（怎么將問題轉化為最優化問題？）

2、轉化為最優化問題的過程？

1）由支持向量X0和模型得到距離d的公式

?2）如何取得d最大？——（轉化問題的最優化量的思想）

>>>問題2：需不需要計算a？

>>>問題3：支持向量是怎么得到的？如何保證它滿足下面的式子？

3）轉化后的最優化問題數學描述（dmax——||w||min）

>>>問題4：以上的限制條件中哪些是已知哪些是未知？

>>>問題5：縮放后的w,b怎么求解？

>>>問題6：限制條件為什么大于等于1？

四、總結

1、機器學習與最優化聯系與區別

1）區別

2）聯系

---

?

---

?

---

?

---

課程鏈接：《浙江大學-研究生機器學習課程》

一、沒有免費的午餐定理

沒有免費的午餐定理：如果我們不對特征空間有先驗假設，則所有算法的平均表現是一樣的。

特征差距小的樣本更有可能是一類

二、支持向量機SVM（support vector machine）

vplink發明的支持向量機

SVM是最大化間隔的分類算法，是一種進行二元分類的廣義線性分類器；SVM也可以通過核方法來對非線性模型進行分類。

1、線性模型和非線性模型

通過一條直線可以將樣本分開為兩個特征的部分叫線性模型，反之叫非線性模型

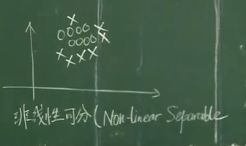
2、如何在線性模型中畫出一條直線（優化過程——vplink）

1）多少條？

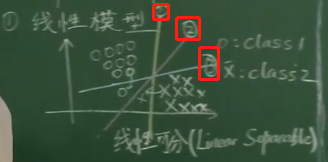
該直線將圓圈和叉區分開，按道理來說有無數條，所以需要找出一條最好的直線

2）如何畫出最好的直線？

先定義一個性能指標，比較每一條直線的性能指標，取性能指標最好的那條線作為最好的直線

這里是以d:間隔（margin）作為性能指標進行分析

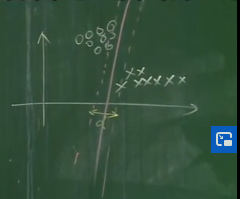
①最優的情形

這里的性能指標是距離——將待定的直線向左和向右移動，直到該直線分別與各特征區域的一個或者多個特征值相交時停止移動，測量這時候兩條直線的距離，取該距離最大的直線為最優直線備選。

但是最優的直線也有無數條，因為與其平行的直線有無數條，該怎么取舍呢？

這時候將直線在d/2處的直線作為最終的直線，作為最優直線

②不是最優的情形

3、如何去描述這個優化的過程（數學描述）

如何去描述這個優化的過程（數學描述）？

1）幾個重要的名詞（間隔、支持向量）

間隔d:margin——最優直線與兩邊最近特征值的距離和叫做間隔

支持向量X0：support vector——被平行線插到的向量叫做支持向量

2）一些定義（訓練數據、標簽、超平面等）

?

訓練數據（XN=【XN1,XN2,XN3,,,XNN】T是一個向量）及標簽(yi是1或-1)：

?

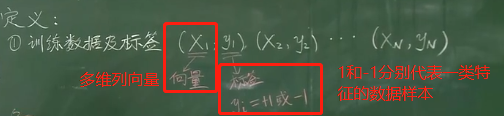
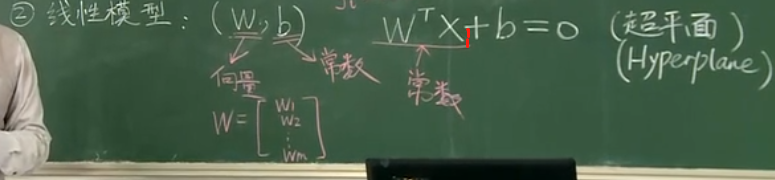
線性模型：（W,b）——待定參數

W的轉置.dot(xi) + b = 0——超平面（Hyperplane）的方程，關于xi的一次線性方程

?

>>>問題1：怎么求解w,b？

答：超平面方程中X=xi,其中i = 1~N,而xi = (xi1,xi2,...,xin)T,因此根據方程可以得到N個方程，N取決于訓練的樣本數，n取決于樣本數的維數，通過求解N個關于w的一次方程組，即可以求解得到w,b，求解方程組的方法有高斯法等，具體可參考《數值分析》

線性模型最優化的任務——在二維的的時候找直線，在三維的時候找平面，在多維的時候找超平面，這里以二維為例

?

?

線性可分：

即：

?

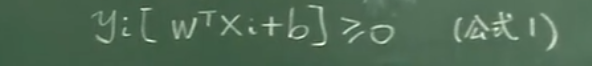
3）機器學習的任務與步驟（求解w,b）

任務（已知（xN,yN），未知（W,b））：

通過這些訓練數據和標簽（（xN,yN）），其中XN = (XN1,XN2,...,XNn)是一個向量，N表示訓練的樣本個數，n表示每一個樣本數的維度；在限定的模型(超平面方程)下，求解出待定系數（W,b），最后確定模型，機器學習的過程也就結束了

?

步驟：

a,通過一個方程來限定模型，如用一個超平面來限定多維模型；

b.在限定的模型中確定待定系數

c.通過訓練數據和限定的模型（方程）求解出待定系數，最后確定模型

三、支持向量機的優化問題（求最優劃分直線，性能指標為d）

1、優化問題（怎么將問題轉化為最優化問題？）

2、轉化為最優化問題的過程？

公式1：

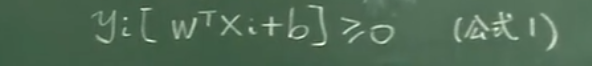
1）由支持向量X0和模型得到距離d的公式

?2）如何取得d最大？——（轉化問題的最優化量的思想）

通過縮放求得d的公式（已知w,b，未知a，也就是后來的aw，ab，支持向量X0未知）：

使得d最大的問題轉化為求||w||的最小值問題

?

>>>問題2：需不需要計算a？

答：不需要！因為這里主要是引入a來講解一下縮放的思想，即告訴我們通過a的縮放能夠將求解d最大值問題轉化為||w||最小值的問題，至于a縮放多少，因為不管a縮放多少，都要假設滿足以下式子（至于為什么這么假設，我也不知道，反正肯定是為了方便計算）：

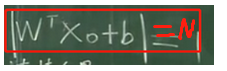
最后d的公式為：

d的公式分子為常數，因此問題dmax依據轉化為求||w||min

?

>>>問題3：支持向量是怎么得到的？如何保證它滿足下面的式子？

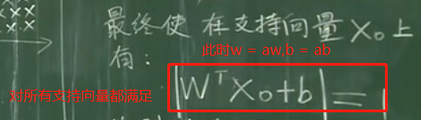
答：這里只是一個假設，實際上支持向量還未知，為我們最優化時的工作，這里只是相當于下了一個定義，限定了a的值來滿足這個假設，最優化的問題就是對縮放后的w進行求解，所以a沒必要進行求解，這里也求不出來

?

3）轉化后的最優化問題數學描述（dmax——||w||min）

凸函數的定義：《最優化課堂筆記04：非線性規劃——凸規劃》

凸函數及二次規劃問題的求解方法：《最優化課程筆記07——約束問題的非線性規劃方法（拉格朗日乘子法和懲罰函數法）》

>>>問題4：以上的限制條件中哪些是已知哪些是未知？

答：已知：xi,yi——即樣本數據，未知——w,b

注意這里要區分開前面通過訓練數據求得的w,b,前面的w,b是一個超平面方程，對所有的訓練數據都滿足，而這里的w,b是在超平面的基礎上進行縮放得到的，雖然平面是一樣的（由事實1得到）：

但是w,b值已經發生了改變，并且這里要求解的w,b是在限制條件下進行求解的，雖然目標函數中看起來只有w,沒有b，但b在限制條件中，如果b的取值不能破壞了約束條件，也是不可以的。

?

>>>問題5：縮放后的w,b怎么求解？

答：先轉化為對偶問題，再使用拉格朗日函數進行求解

?

?

>>>問題6：限制條件為什么大于等于1？

答：首先根據線性可分性得到限制條件必然大于等于0，又因為問題dmax轉化為||w||min的問題時在支持向量上滿足，

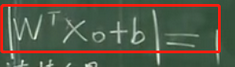
所以在非支持向量上有：yi=1時，平面方程的模會大于1;即：

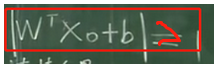
yi=-1時，平面方程的模會小于-1，即：

所以二者相乘就會大于等于1，當然也可以大于等于任何的正整數N，此時a的縮放就應該滿足：

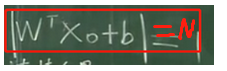
結果一致，一般是大于等于1

四、總結

1、機器學習與最優化聯系與區別

1）區別

機器學習：通過已知的訓練數據在限定的模型下求解出模型的待定系數，得到這個問題的一個確切具體的模型，重點在于求解模型的待定系數w,b，求得的w,b只是滿足了將二元分類了，但不一定是最優的分類平面

最優化：求解出問題的最優解，即找到最優的分類平面

2）聯系

機器學習包含了最優化，其實機器學習就是在不斷地對數據進行優化，得到最優解。起初機器學習是通過現有的訓練數據得到一個模型，后面再通過學習（優化）求得最優解。

?

?

非線性模型的最優化問題該怎么求解呢？請看：《機器學習理論——支持向量機SVM之非線性模型》

?

還可以參考：《[機器學習筆記] 支持向量機SVM如何求解最佳模型？》