目錄
一、復習(原問題、對偶問題、KKT條件、凸函數)
二、將最優化問題標準化為原問題(嚴格轉化為標準形式)
1、原最優化問題
2、標準化后的問題
三、轉化為對偶問題(注意變量的對應關系)
四、對對偶問題的目標函數進行簡化(利用L函數的偏導)
1、L函數
2、對L函數各待定系數求偏導
1)向量求導
2)L函數求偏導
3、對偶問題目標函數簡化(將fai用核函數K替換)
1)由后面兩個偏導等式可以將L化簡為:
2)再通過第一個偏導等式進一步化簡:
3)L函數最終簡化形式——對偶問題的簡化形式
五、回歸原問題求解w和b
1、求解w
2、求解b
六、SVM算法總結(訓練+測試)
1、訓練流程(根據訓練樣本求解b,獲得最優化模型)
2、測試流程(利用最優化模型對新的樣本進行分類)
七、易產生的疑惑
1、原問題是求解w,b,為什么后面只需要求b就好了,原問題的最優解不管了嗎?
一、復習(原問題、對偶問題、KKT條件、凸函數)


二、將最優化問題標準化為原問題(嚴格轉化為標準形式)
1、原最優化問題

2、標準化后的問題
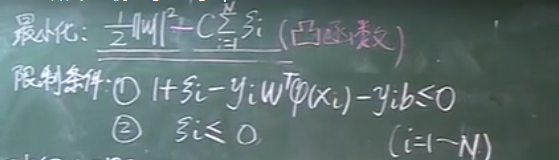
?
三、轉化為對偶問題(注意變量的對應關系)
注:這里的w指的是問題中的待定系數,如在非線性問題中w代表的是w、b和松弛變量
注:這里的α表示的是原問題中限制條件中不等式約束中的待定系數,如下面α有兩個變量因為有兩個不等式約束;β表示原問題中限制條件中等式約束中的待定系數,如下面β沒有,因為沒有等式約束。

四、對對偶問題的目標函數進行簡化(利用L函數的偏導)
1、L函數
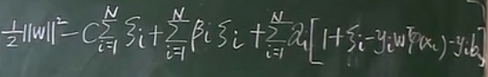
2、對L函數各待定系數求偏導
1)向量求導
?

2)L函數求偏導
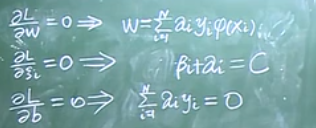
3、對偶問題目標函數簡化(將fai用核函數K替換)
將L函數求偏導得到的等式都帶入到L函數中,可以將L函數進行簡化,也就是對對偶問題的目標函數進行了簡化

1)由后面兩個偏導等式可以將L化簡為:

2)再通過第一個偏導等式進一步化簡:
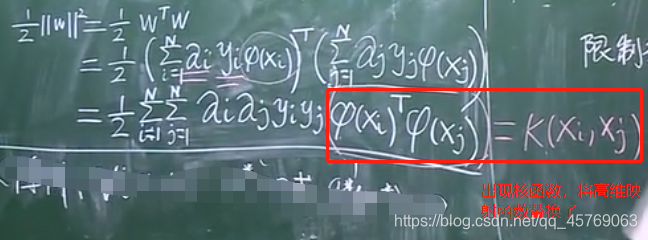
上面只有fai是向量,其余的均為標量
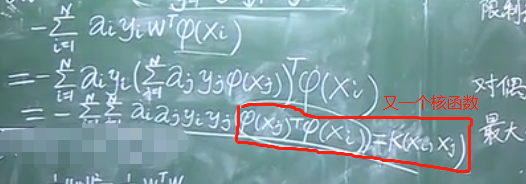
3)L函數最終簡化形式——對偶問題的簡化形式

求解以上問題的算法稱為:SMO算法
五、回歸原問題求解w和b
>>>問題1:原問題是為了求解W,b,但是上面經過對偶化后求解的卻是α和β,那w,b該怎么返回去求解?

1、求解w
根據測試流程實際上不需要知道w的確切值,只需要知道上圖等式和0的關系即可
由L函數對w求偏導=0的等式和核函數來進行計算。
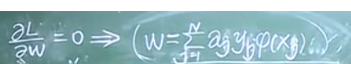
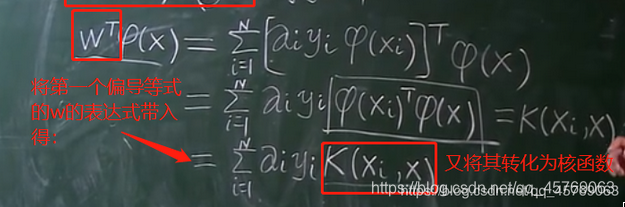
2、求解b
通過KKT條件和核函數來對b進行求解:
KKT條件
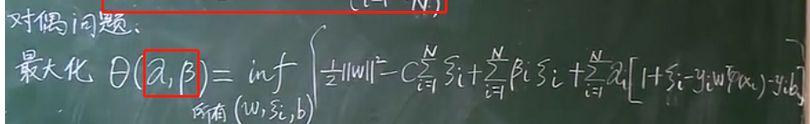

求得b
?
六、SVM算法總結(訓練+測試)
1、訓練流程(根據訓練樣本求解b,獲得最優化模型)
已知:yi,yj,xi,xj,K(xi,xj)
未知:αi,αj,b
求解αi,αj可以用《SMO算法》進行求解,求解b利用公式即可求解

實際情況下求解b時,會選取多個α的值求得多個b,然后將多個b的值進行平均化,將平均值作為b最終的取值
2、測試流程(利用最優化模型對新的樣本進行分類)

七、易產生的疑惑
1、原問題是求解w,b,為什么后面只需要求b就好了,原問題的最優解不管了嗎?
答:剛開始我也有這個疑惑,以為是通過對偶化作為一種手段來求解原問題的最優解w,b。這里我們不能拘泥于解方程,而是得記住最終的目的,為什么求解w,b呢?即使為了得到最優化的模型,而得到的模型是為了對新的樣本數據實現標簽分類(y=1或y=-1),這才是機器學習的真正目的所在,通過對偶化我們將原問題求解w,b轉化為了求解核函數以及b,最終依然得到了最優化的模型,利用該模型可以對新的樣本數據進行分類!!!這里也就是說最終我們得到的是一個SVM模型,或者說我們通過訓練樣本訓練出來了一個SVM模型,利用這個模型我們就可以對測試樣本進行分類啦

-模糊查找)




)





)




)

