目錄

一、原問題（prime problem）

二、原問題的對偶問題（dual problem）

1、定義一個輔助函數

2、定義對偶問題

>>>問題1：上面說到遍歷w，那w的取值范圍和取值步長是怎樣的？即遍歷的w從何處求得？

3、原問題與對偶問題解的關系（一個定理）

4、原問題與對偶問題的間距G——Duality gap（定義）

5、強對偶定理（G=0的特定情況）

6、KKT條件（由強對偶定理反推出的條件）

---

課程鏈接：《浙江大學-研究生機器學習課程》

上接：《支持向量機SVM之非線性模型（低維映射到高維）》

一、原問題（prime problem）

注：這里的w指的是問題中的待定系數，如在非線性問題中w代表的是w、b和松弛變量

二、原問題的對偶問題（dual problem）

1、定義一個輔助函數

注：這里的α表示的是原問題中限制條件中不等式約束中的待定系數；β表示原問題中限制條件中等式約束中的待定系數

2、定義對偶問題

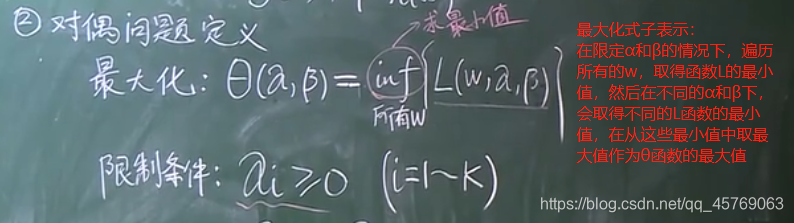
>>>問題1：上面說到遍歷w，那w的取值范圍和取值步長是怎樣的？即遍歷的w從何處求得？

答：這里不需要求解，只是為了下一個定義罷了，具體繼續往下看

3、原問題與對偶問題解的關系（一個定理）

4、原問題與對偶問題的間距G——Duality gap（定義）

5、強對偶定理（G=0的特定情況）

?

6、KKT條件（由強對偶定理反推出的條件）

具體如何將原問題轉化為對偶問題，進而求解原問題：

《機器學習理論——支持向量機SVM之非線性模型（原問題轉化為對偶問題）》