目錄

一、非線性模型的最優化問題

1、非線性模型最優化模型

2、兩個概念

1）正則項（regularization term）

2）調參參數

2、高維映射

1）定義及作用

2）高維映射后的最優化模型

3）異或問題（例子）

4）如何定義映射？（尋找確定映射關系——核函數的確定）

核函數與高維映射的關系：

常用核函數：

核函數K可以拆寫成高維映射的內積的條件：

二、總結

如何通過核函數來代替優化問題中限制條件中的高維映射進而對最優化問題進行求解呢？

---

課程鏈接：《浙江大學-研究生機器學習課程》

一、非線性模型的最優化問題

至于什么是非線性方程在《機器學習理論——支持向量機SVM之線性模型》中已經講過，不再贅述

1、非線性模型最優化模型

在線性模型的基礎上，添加一個正則項和改變限制條件就得到了非線性模型

已知量：訓練數據——xi，標簽——yi，系數——C；

未知量：權重系數——w，偏置——b，松弛變量——（slack variable）

2、兩個概念

1）正則項（regularization term）

正則項使得目標函數規劃化，讓沒有解的問題變得有解（如線性模型在非線性情況下就沒有解，這時候加上合適的正則項后有解可取），或者求得的解不是我們所需要的解的時候則我們需要進行正則項的添加

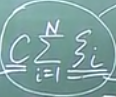
2）調參參數

C是事先設定好的值，作用是用來對目標函數w和松弛變量間進行權衡的作用，是一個權重。那具體取什么值呢？一般取值沒有固定的取值，C的大小決定了模型分類時容錯率的大小，C越大，說明容錯率越小，越小則表明容錯率越大，容錯率就是沒有正確被歸類的占比

2、高維映射

1）定義及作用

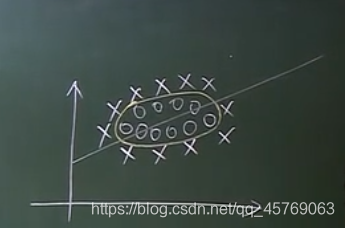
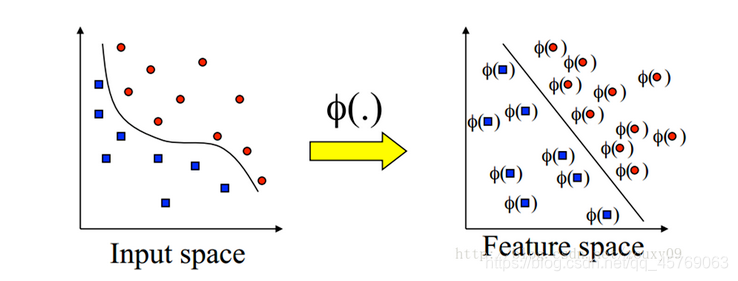
在非線性模型中尋找一條直線進行二元分類似乎已經不太適用（如上圖找不到直線進行二元分類），但是通過映射，將低維的量映射到高維，即通過高維映射后，在高維空間中，更有可能線性可分進行二元分類。維度越高，線性可分的概率越大

2）高維映射后的最優化模型

3）異或問題（例子）

異或問題是最簡單的非線性模型，在低維下沒法找到一條直線將二元分類

其中一個解：

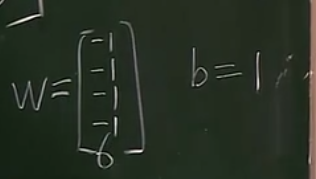
驗證結果正確性（判斷是否線性可分）

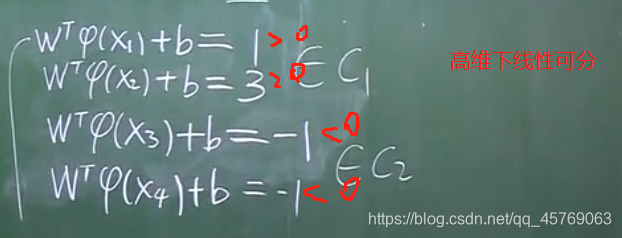
注：

維度越高，線性可分的概率越大

維數為無限時，線性可分的概率為1

?

4）如何定義映射？（尋找確定映射關系——核函數的確定）

主要思路：我們不需要知道映射的確切關系，只需要知道由低維樣本組成的核函數的形式即可，因為核函數可以拆分為高維映射的內積

核函數與高維映射的關系：

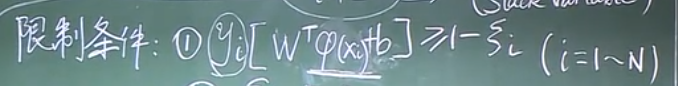
常用核函數：

核函數K可以拆寫成高維映射的內積的條件：

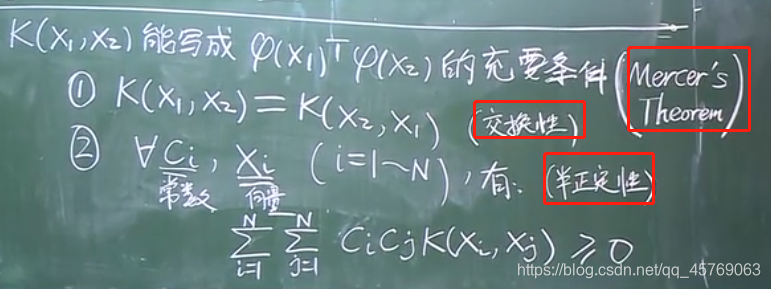
二、總結

這節主要給出了非線性模型最優化問題，以及非線性最優化問題求解的思路——高維映射，利用核函數替代最優化問題中的高維映射進行求解

如何通過核函數來代替優化問題中限制條件中的高維映射進而對最優化問題進行求解呢？

請看：《機器學習理論——支持向量機SVM之非線性模型（原問題和對偶問題）》