?
目錄
?
論文名稱:Deep Residual Learning for Image Recognition?
摘要:
1、引言
2、為什么會提出ResNet殘差網絡呢?
3、深度殘差網絡結構學習(Deep?Residual?learning)
(1)殘差單元
(2)恒等映射/單位映射(identity?mapping)
(3)瓶頸(BottleNeck)模塊
(4)ResNet的結構
? (5)ResNet的進一步改進
參考博客:
轉載:https://www.cnblogs.com/xiaoboge/p/10539884.html(個人覺得這篇博客寫的很詳細,對于殘差網絡的原理和優勢進行了詳細的解釋)
紅色部分為自己添加
論文名稱:Deep Residual Learning for Image Recognition?
?作者:微軟亞洲研究院的何凱明等人? ? ? ? ? ? ?論文地址:https://arxiv.org/pdf/1512.03385v1.pdf
摘要:
隨著人們對于神經網絡技術的不斷研究和嘗試,每年都會誕生很多新的網絡結構或模型。這些模型大都有著經典神經網絡的特點,但是又會有所變化。你說它們是雜交也好,是變種也罷,總之針對神經網絡的創新的各種辦法那真叫大開腦洞。而這些變化通常影響的都是使得這些網絡在某些分支領域或者場景下表現更為出色(雖然我們期望網絡的泛化性能夠在所有的領域都有好的表現)。深度殘差網絡(deep?residual?network)就是眾多變種中的一個代表,而且在某些領域確實效果不錯,例如目標檢測(object?detection)。
1、引言
2015年時,還在MSRA的何愷明祭出了ResNet這個“必殺技”,在ISLVRC和COCO上“橫掃”了所有的對手,可以說是頂級高手用必殺技進行了一場殺戮。除了取得了輝煌的成績之外,更重要的意義是啟發了對神經網絡的更多的思考。可以說深度殘差網絡(Deep residual network, ResNet)的提出是CNN圖像史上的一件里程碑事件。
ResNet的作者何愷明獲得了CVPR2016最佳論文獎。那么ResNet為什么會如此優異的表現呢?其實ResNet是解決了深度CNN模型難訓練的問題,我們知道2014年的VGG才19層,而15年的ResNet多達152層,這在網絡深度完全不是一個量級上,所以如果是第一眼看到這個層數的話,肯定會覺得ResNet是靠深度取勝。事實當然是這樣,但是ResNet還有架構上的trick,這才使得網絡的深度發揮出作用,這個trick就是殘差學習(Residual learning)。接下來我們將詳細分析ResNet的原理。
?
2、為什么會提出ResNet殘差網絡呢?
add:
??????? VGGNet和Inception出現后,大家都想著通過增加網絡深度來尋求更加優秀的性能,但是網絡的加深也帶來了一定的困難,如:
??????? 1)網絡加深導致參數增加,導數網絡難以訓練;
??????? 2)因為網絡太深,導致根據梯度鏈條傳遞原則,使得傳播到淺層時,梯度消失;也可能出現梯度爆炸的情況,但是通過BN層歸一化到【0,1】之間已經很好地解決了梯度爆炸的現象
??????? 3)越深的網絡梯度相關性差,接近白噪聲,導致梯度更新也接近于隨機擾動
??????? 綜上可知:要想更加深的網絡進行訓練,并且獲得良好的性能,我們首要需要解決的就是使得深層的梯度能夠傳遞到淺層來,這樣才能使得網絡參數能夠有效的更新,其實就是抑制梯度損失
VGG網絡試著探尋了一下深度學習網絡的深度究竟可以深到何種程度還可以持續提高分類的準確率。對于傳統的深度學習網絡,我們普遍認為網絡深度越深(參數越多)非線性的表達能力越強,該網絡所能學習到的東西就越多。我們憑借這一基本規則,經典的CNN網絡從LetNet-5(5層)和AlexNet(8層)發展到VGGNet(16-19),再到后來GoogleNet(22層)。根據VGGNet的實驗結果可知,在某種程度上網絡的深度對模型的性能至關重要,當增加網絡層數后,網絡可以進行更加復雜的特征模式的提取,所以當模型更深時理論上可以取得更好的結果,從圖1中也可以看出網絡越深而效果越好的一個實踐證據。
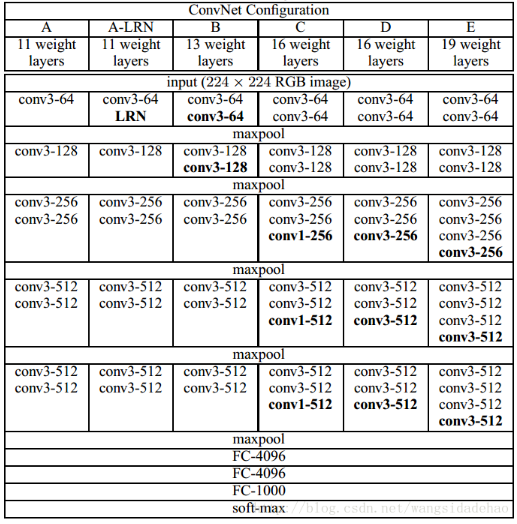

?? ? ?????????????????????????????????????????? 圖1:VGGNet網絡結構和實驗結果
? 但是更深的網絡其性能一定會更好嗎?我們后來發現傳統的CNN網絡結構隨著層數加深到一定程度之后,越深的網絡反而效果更差,過深的網絡竟然使分類的準確率下降了(相比于較淺的CNN而言)。比較結果如圖2。

?
圖2:常規的CNN網絡過分加深網絡層數會帶來分類準確率的降低
為什么CNN網絡層數增加分類的準確率卻下降了呢?難道是因為模型參數過多表達能力太強出現了過擬合?難道是因為數據集太小出現過擬合?顯然都不是!!!我們來看,什么是過擬合呢?過擬合就是模型在訓練數據上的損失不斷減小,在測試數據上的損失先減小再增大,這才是過擬合現象。根據圖2?的結果可以看出:56層的網絡比20層網絡在訓練數據上的損失還要大。這可以肯定不會是過擬合問題。因此,我們把這種問題稱之為網絡退化問題(Degradation problem)。
我們知道深層網絡存在著梯度消失或者爆炸的問題,這使得深度學習模型很難訓練。但是現在已經存在一些技術手段如BatchNorm來緩解這個問題。因此,出現深度網絡的退化問題是非常令人詫異的。
何愷明舉了一個例子:考慮一個訓練好的網絡結構,如果加深層數的時候,不是單純的堆疊更多的層,而是堆上去一層使得堆疊后的輸出和堆疊前的輸出相同,也就是恒等映射/單位映射(identity?mapping),然后再繼續訓練。這種情況下,按理說訓練得到的結果不應該更差,因為在訓練開始之前已經將加層之前的水平作為初始了,然而實驗結果結果表明在網絡層數達到一定的深度之后,結果會變差,這就是退化問題。這里至少說明傳統的多層網絡結構的非線性表達很難去表示恒等映射(identity?mapping),或者說你不得不承認目前的訓練方法或許有點問題,才使得深層網絡很難去找到一個好的參數去表示恒等映射(identity?mapping)。
?
3、深度殘差網絡結構學習(Deep?Residual?learning)
(1)殘差單元
這個有趣的假設讓何博士靈感爆發,他提出了殘差學習來解決退化問題。對于一個堆積層結構(幾層堆積而成)當輸入為x時其學習到的特征記為H(x),現在我們希望其可以學習到殘差F(x) = H(x) - x,這樣其實原始的學習特征是H(x)。之所以這樣是因為殘差學習相比原始特征直接學習更容易。當殘差為F(x) = 0時,此時堆積層僅僅做了恒等映射,至少網絡性能不會下降,實際上殘差不會為0,這也會使得堆積層在輸入特征基礎上學習到新的特征,從而擁有更好的性能。殘差學習的結構如圖3所示。這有點類似與電路中的“短路”,所以是一種短路連接(shortcut connection)。

圖3:殘差學習單元
為什么殘差學習相對更容易,從直觀上看殘差學習需要學習的內容少,因為殘差一般會比較小,學習難度小點。不過我們可以從數學的角度來分析這個問題,首先殘差單元可以表示為:

?
其中,XL和XL+1分別表示第L個殘差單元的輸入和輸出,注意每個殘差單元一般包含多層結構。F是殘差函數,表示學習到的殘差,而h(XL) = XL表示恒等映射,f 是ReLu激活函數。基于上式,我們求得從淺層 l?到深層 L?的學習特征。

?
?我們可以知道,對于傳統的CNN,直接堆疊的網絡相當于一層層地做——仿射變換-非線性變換,而仿射變換這一步主要是矩陣乘法。所以總體來說直接堆疊的網絡相當于是乘法性質的計算。而在ResNet中,相對于直接堆疊的網絡,因為shortcut的出現,計算的性質從乘法變成了加法。計算變的更加穩定。當然這些是從前向計算的角度,從后向傳播的角度,如果代價函數用Loss表示,則有
增加短路連接shortcut_connection后的梯度(1表示能夠將損失無損地傳遞到上一層,而殘差項需要經過w卷積層等,結合圖3:殘差學習單元來理解)

未增加短路連接的梯度表達式(當網絡很深時傳到淺層殘差 會很小,導致梯度會有消失的風險):
會很小,導致梯度會有消失的風險):
??????????????????????? 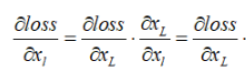

下面這段話很重要,因為通過一個短路連接使得梯度能夠比較完整的傳遞到上一層,雖然有殘差項,但是梯度比沒有短路前更加完整,從而使得梯度的衰減進一步得到了抑制,這樣使得從深層反向傳播回來的梯度不至于消失,這也為增加更多層實現更深層的神經網絡提供了可行性的保障。
也就是說,無論是哪層,更高層的梯度成分![]() 都可以直接傳過去。小括號中的1表明短路機制(shortcut)可以無損地傳播梯度,而另外一項殘差梯度則需要經過帶有weights的層,梯度不是直接傳遞過來的。殘差梯度
都可以直接傳過去。小括號中的1表明短路機制(shortcut)可以無損地傳播梯度,而另外一項殘差梯度則需要經過帶有weights的層,梯度不是直接傳遞過來的。殘差梯度![]() 不會那么巧全為-1,而且就算其比較小,有1的存在也不會導致梯度消失。這樣一來梯度的衰減得到進一步抑制,并且加法的計算讓訓練的穩定性和容易性也得到了提高。所以可訓練的網絡的層數也大大增加了。
不會那么巧全為-1,而且就算其比較小,有1的存在也不會導致梯度消失。這樣一來梯度的衰減得到進一步抑制,并且加法的計算讓訓練的穩定性和容易性也得到了提高。所以可訓練的網絡的層數也大大增加了。
(2)恒等映射/單位映射(identity?mapping)
我們知道殘差單元通過 identity?mapping?的引入在輸入和輸出之間建立了一條直接的關聯通道,從而使得強大的有參層集中學習輸入和輸出之間的殘差。一般我們用F(X, Wi)來表示殘差映射,那么輸出即為:Y = F(X, Wi) + X 。當輸入和輸出通道數相同時,我們自然可以如此直接使用X進行相加。而當它們之間的通道數目不同時,我們就需要考慮建立一種有效的 identity mapping 函數從而可以使得處理后的輸入X與輸出Y的通道數目相同即Y = F(X, Wi) + Ws*X。
當X與Y通道數目不同時,作者嘗試了兩種 identity mapping 的方式。一種即簡單地將X相對Y缺失的通道直接補零從而使其能夠相對齊的方式,另一種則是通過使用1x1的conv來表示Ws映射從而使得最終輸入與輸出的通道達到一致的方式。
(3)瓶頸(BottleNeck)模塊
如下圖4所示,左圖是一個很原始的常規模塊(Residual block),實際使用的時候,殘差模塊和Inception模塊一樣希望能夠降低計算消耗。所以論文中又進一步提出了“瓶頸(BottleNeck)”模塊,思路和Inception一樣,通過使用1x1 conv來巧妙地縮減或擴張feature map維度(也就是改變channels通道數)從而使得我們的3x3 conv的filters數目不受外界即上一層輸入的影響,自然它的輸出也不會影響到下一層module。不過它純是為了節省計算時間進而縮小整個模型訓練所需的時間而設計的,對最終的模型精度并無影響。

?
圖4:BottleNeck模塊
(4)ResNet的結構
創新點:
1)短路連接,使得梯度消失得到了一定的改善
2)圖像輸入直接使用了步長為2進行下采樣
3)使用全局平均池化代替了全連接層
4)當特征圖大小發生倍數變化時,其個數也會發生相應的倍數變換,比如大小減半則數量會增倍,保證了網絡結構的復雜度
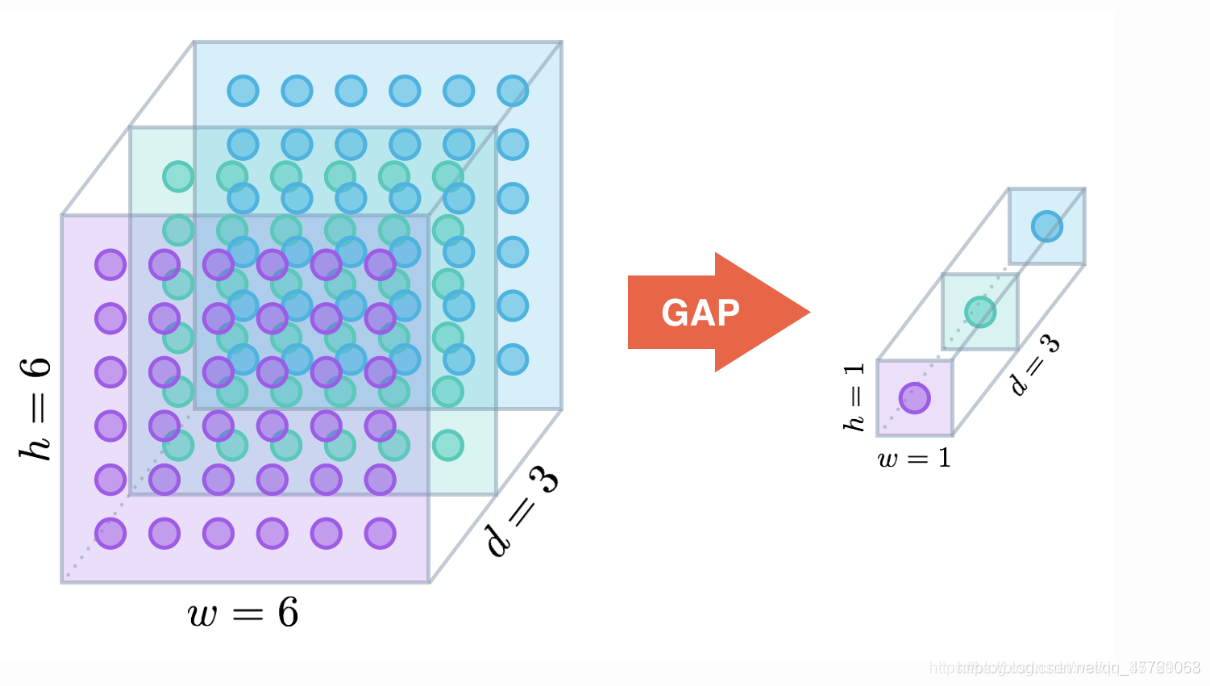
何為全局平均池化?
全局平均池化其實就是將最后一層每個通道取均值,最終變成channels * 1 * 1的一維格式,這樣的效果和全連接層是一致的
圖片來自:https://blog.csdn.net/weixin_37721058/article/details/96573673
ResNet網絡是參考了VGG19的網絡,在其基礎上進行了修改,并通過短路機制加入了殘差單元,如圖5所示。變化主要體現在ResNet直接使用stride=2的卷積做下采樣,并且用global average pool層替換了全連接層。ResNet的一個重要設計原則是:當feature map大小降低一半時,featuremap的數量增加一倍,這保持了網絡層的復雜度。從圖5中可以看到,ResNet相比普通網絡每兩層間增加了短路機制,這就形成了殘差學習,其中虛線表示featuremap數量發生了改變。圖5展示的34-layer的ResNet,還可以構建更深的網絡如表1所示。從表中可以看到,對于18-layer和34-layer的ResNet,其進行的兩層間的殘差學習,當網絡更深時,其進行的是三層間的殘差學習,三層卷積核分別是1x1,3x3和1x1,一個值得注意的是隱含層的feature map數量是比較小的,并且是輸出feature map數量的1/4。

圖5 ResNet網絡結構圖
?
表1?不同深度的ResNet
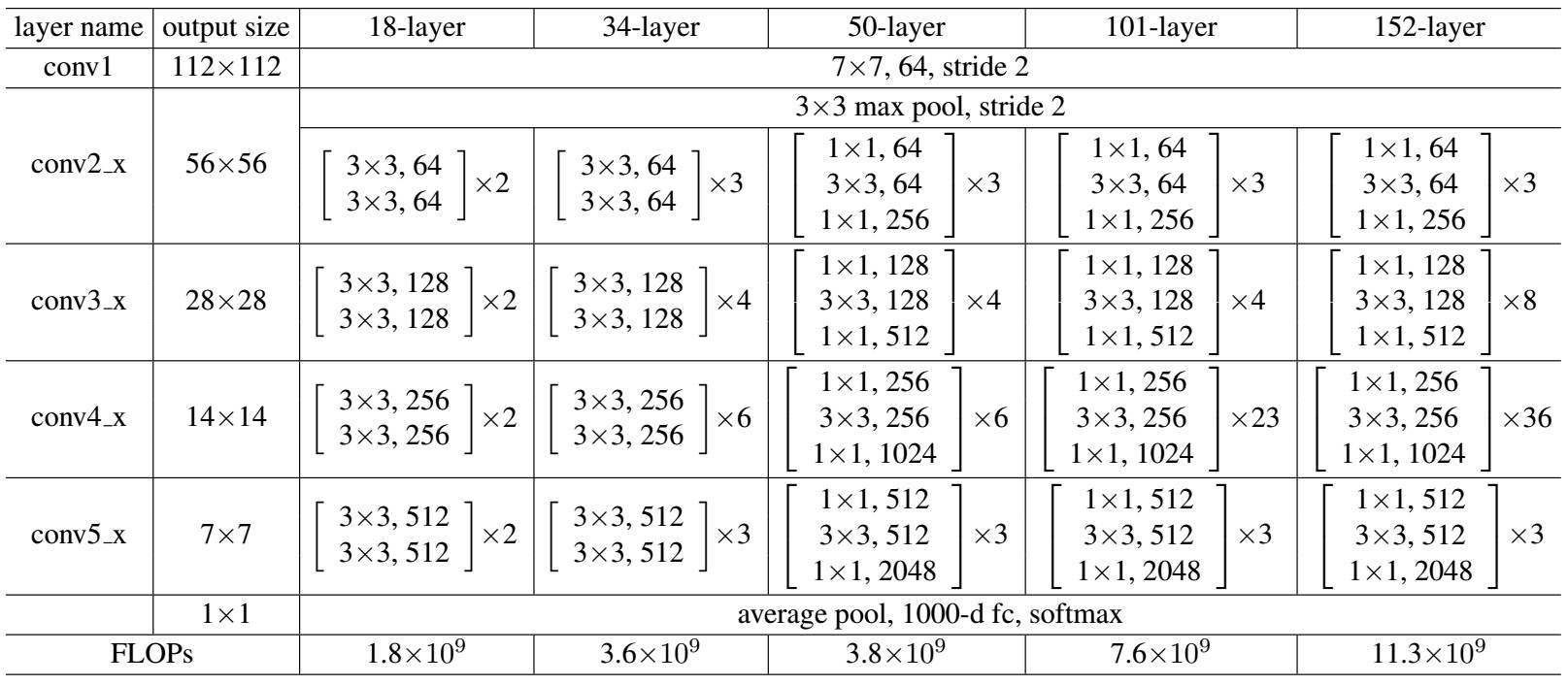
?
下面我們再分析一下殘差單元,ResNet使用兩種殘差單元,如圖6所示。左圖對應的是淺層網絡,而右圖對應的是深層網絡。對于短路連接,當輸入和輸出維度一致時,可以直接將輸入加到輸出上。但是當維度不一致時(對應的是維度增加一倍),這就不能直接相加。有兩種策略:
(1)采用zero-padding增加維度,此時一般要先做一個downsamp,可以采用strde=2的pooling,這樣不會增加參數;
(2)采用新的映射(projection shortcut),一般采用1x1的卷積,這樣會增加參數,也會增加計算量。短路連接除了直接使用恒等映射,當然都可以采用projection shortcut。
圖6?不同的殘差單元
作者對比18-layer和34-layer的網絡效果,如圖7所示。可以看到普通的網絡出現退化現象,但是ResNet很好的解決了退化問題。
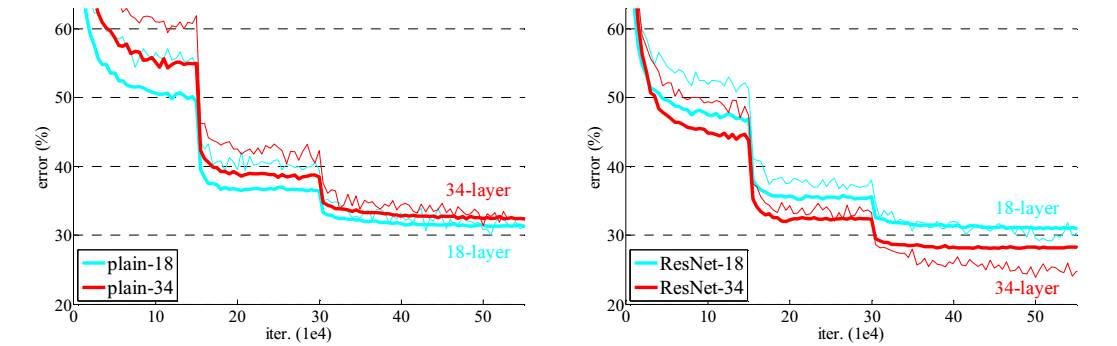
圖7 18-layer和34-layer的網絡效果
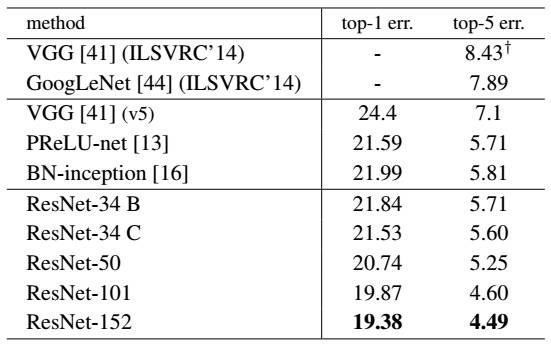
最后展示一下ResNet網絡與其他網絡在ImageNet上的對比結果,如表2所示。可以看到ResNet-152其誤差降到了4.49%,當采用集成模型后,誤差可以降到3.57%。
表2 ResNet與其他網絡的對比結果
?
? (5)ResNet的進一步改進
? 在2015年的ILSVRC比賽獲得第一之后,何愷明對殘差網絡進行了改進,主要是把ReLu給移動到了conv之前,相應的shortcut不在經過ReLu,相當于輸入輸出直連。并且論文中對ReLu,BN和卷積層的順序做了實驗,最后確定了改進后的殘差網絡基本構造模塊,如下圖8所示,因為對于每個單元,激活函數放在了仿射變換之前,所以論文叫做預激活殘差單元(pre-activation residual unit)。作者推薦在短路連接(shortcut)采用恒等映射(identity?mapping)。
?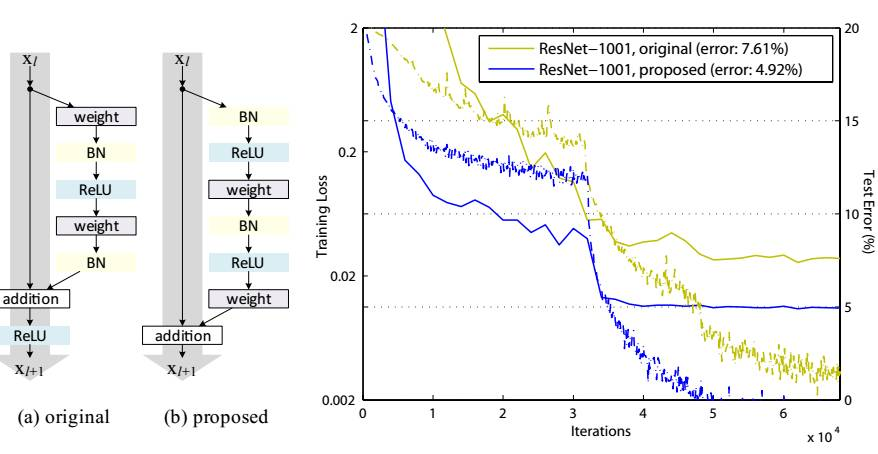
圖8?改進后的殘差單元及效果
參考博客:
?
你必須要知道的CNN模型ResNet:https://blog.csdn.net/u013709270/article/details/78838875
經典分類CNN模型系列其四:https://www.jianshu.com/p/93990a641066



)












?是誰?))


