寫給自己看的學習記錄：

光具有波粒二象性，由此衍生出了幾何光學與衍射光學。在光學設計軟件中，最常用的判斷標準是查看點列圖的RMS半徑以及MTF圖的曲線，這兩者分別代表了兩種傳播性質的評價方式。

在剛接觸光學設計時，我誤認為評價標準是，將RMS半徑優化到小于像元尺寸的一半即可。認為點列圖好了，MTF肯定也好了，其實這是不對的，忽視了艾里斑是最小光斑的衍射理論。

后來才了解到，當點列圖小于艾里斑時，RMS半徑便不再可靠。用zemax軟件優化過程中，主要就是衍射與幾何相互對抗的過程，當RMS半徑值遠大于艾里斑半徑時，主要看點列圖；當點列圖滿足要求時，盡量把MTF曲線往衍射極限上優化。

艾里斑半徑R=1.22λF，由于λ是設計要求，那么F的選取就很重要，艾里斑過大或者過小都會帶來問題，一般來說，讓艾里斑半徑等于所選探測器的像元尺寸。

具體原因在

薇洛的打火機/衍射極限、MTF與相機分辨率(1)這篇博客里有很詳細的介紹。

大致如下：

在空間域中，成像系統的光斑是理想圖像與點擴散函數h(t)卷積的結果，而調制傳遞函數MTF就是系統點擴散函數h(t)經過Fourier變換的結果。

MTF是一個頻域的概念，代表不同頻率成分對比度的衰減，在光學評價方法中，它的單位是lp/mm，即每毫米/線對，代表每mm范圍內，有幾個明暗相間的正弦條紋。測試一個光學系統的MTF，就是測試對不同疏密(lp/mm為單位)的條紋的對比度衰減。（lp/mm通常是指像平面上的線對數。）

根據Shannon采樣定理，對于頻率為f 的信號，我們至少要用2f的頻率來采樣，才能把它恢復出來。從前面的敘述，我們知道，空間頻率一般是用探測器上每毫米線對數來表示的，我們至少需要兩個像素來采樣它，即兩個像素尺寸對應一個線對寬度。這也就是光學設計中奎奈斯特截止頻率計算公式的由來，即：

截止頻率=1/（2*像元尺寸）

那么回到最初的問題，艾里斑多大才與我們的像元尺寸相匹配，這決定了我們光學設計中F數的選擇。

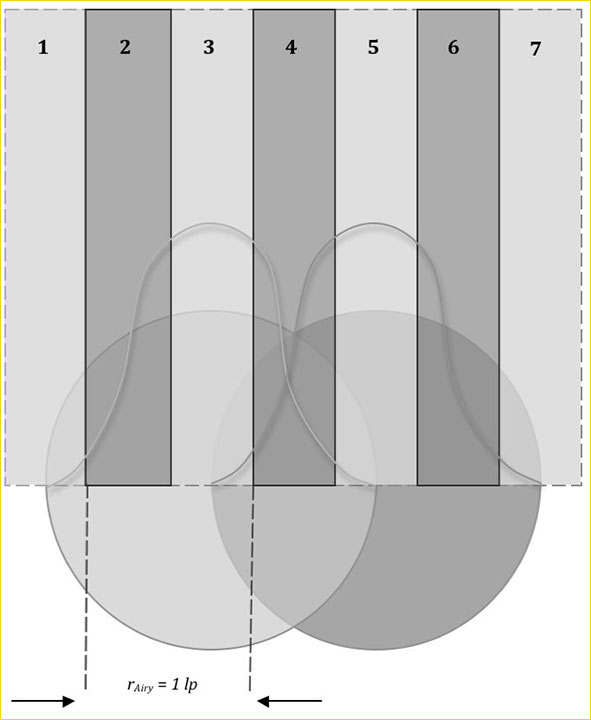
根據瑞利判據，當兩個相鄰的艾里斑距離為其半徑時，這兩個艾里斑勉強能夠分辨出來。

即一個線對寬度等于艾里斑的半徑，在這個頻率往上，系統是衍射受限的。哪怕沒有任何像差，MTF都很差，細節幾乎不可分辨。

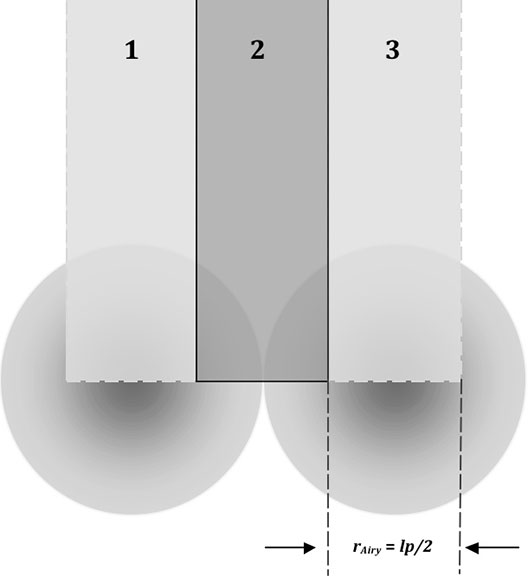
即艾里斑直徑最大不能超過兩個像元尺寸，否則該系統將無意義。

但是在設計中，沒必要做的這么極限，另外還要考慮公差對像質的影響。

所以，一般取線對寬度等于艾里斑的直徑，即一個像元尺寸等于艾里斑的半徑，此時截止頻率處衍射極限的MTF值約為0.5，是可以接受的。

?當然艾里斑可以更小，這樣截止頻率處的MTF值會更高，但是F數太大在光學設計中是件很頭疼的事，各種像差帶來的影響也很難使MTF接近衍射極限。

畢竟光學設計本身就是一件不斷取舍的工作。

所以我們在設計中，常取F數，使得艾里斑半徑等于像元尺寸大小即可。

注1：在紅外設計中，將點列圖優化到艾里斑內并將MTF曲線優化到接近衍射極限即可，不必太關注RMS半徑值。

注2：在需求中，F數是有要求的，比如紅外常要做到F1.0，反過來即可，即挑選合適的探測器。如果探測器也選定，且像元尺寸很小，那只能BIN了，犧牲分辨率。

注3：原文鏈接：https://blog.csdn.net/glorydream2015/article/details/44966369

（原文作者的一個例子，懶得打字，直接引用）

對于一個F數為2.8的鏡頭，假設我們用555nm的黃綠光來成像，像素大小做到多少合適呢？我們取線對寬度等于艾里斑的直徑大小作為依據，此時只考慮衍射的話，MTF約有0.5，也還算可以了。一個線對對應兩個像素，那么一個像素大小就相當于艾里斑的半徑，也就是1.22λF，算出來約為1.9微米。如果固定傳感器大小的話，那么它的像素數就是有上限的。到達一個限度，再增加像素數，就會導致像素小于1.9微米，再增加的像素已經提供不了新的信息了。

（批注：即艾里斑半徑大于一個像素，像素和像素之間是模糊的，如果BIN的話，其實還是分辨率變少，所以現在市場上的超高像素相機或者手機實在是噱頭，以致于只能宣傳BIN的好處。）

?