目錄
常見的三種排序方法
冒泡排序
插入排序
選擇排序
其他經典的排序方法
快速排序
堆排序
歸并排序
?希爾排序
?不同排序方法的各維度對比
排序方式的穩定性:若兩個相同的元素在排序前后的相對位置不發生改變的排序為穩定排序,否則不穩定排序
常見的三種排序方法
以【3,2,2,1,1】為例
冒泡排序
冒泡排序思路:不斷地對比相鄰的兩個元素,將若前面的元素 大于(注意不含等于) 后面的元素,則兩個元素進行位置交換。
# 冒泡排序,復雜度為O(n^2)
def bubble_sorted(li:list)->list:for i in range(len(li)):# 第幾趟exchanged = False# 這個是為了防止多余的遍歷,如果前面的元素已經是排序好的,那就不需要再進行比較了,減少運行時間for j in range(len(li)-1):# 遍歷列表元素if li[j] > li[j+1]:li[j],li[j+1] = li[j+1],li[j]exchanged = Trueif not exchanged:return li
第一趟
| 3 | 2(1) | 2(2) | 1(1) | 1(2) |
|---|---|---|---|---|
| 2(1) | 3 | 2(2) | 1(1) | 1(2) |
| 2(1) | 2(2) | 3 | 1(1) | 1(2) |
| 2(1) | 2(2) | 1(1) | 3 | 1(2) |
| 2(1) | 2(2) | 1(1) | 1(2) | 3 |
第二趟
第三趟
第四趟? 、第五趟、第六趟
可見在經過冒泡排序后,相同元素的相對前后位置沒有發生改變 ,因此排序是穩定的。
插入排序
插入排序的思路:從左到右,分為有序區和無序區,每次都是將無序區的第一個元素取出插入到有序區間中。然后從右往左遍歷有序區,當遍歷的有序元素大于該元素時,有序元素右移一位,繼續遍歷有序區;直到遍歷的有序元素小于等于無序區元素第一個元素時,停止遍歷,并且將該元素插入到停止遍歷有序元素的后一個位置
# 插入排序,復雜度為O(n^2),思路是從左到右抽取一個元素,將這個元素,與左邊鄰近的元素比較,若比左邊的小,則左邊元素右移,
# 若不比左邊的小了或者已經到最左邊了,則將抽取的元素賦值給原本左邊元素
def insert_sorted(li:list)->list:for i in range(1,len(li)):# 趟數,也就是抽牌的順序,從第一張牌開始抽tmp = li[i]j = i - 1# 左邊元素while j >= 0 and li[i] < li[j]:# 若抽取的元素小于鄰近左邊的元素,則將左邊元素右移一格li[j+1] = li[j]j -= 1# 這時候的j已經不滿足上述條件了,因此這個j位置上的元素沒有移動,而j+1上位置的元素移動了是空的li[j+1] = tmpreturn li| 3 | 2(1) | 2(2) | 1(1) | 1(2) |
|---|---|---|---|---|
| 2(1) | 3 | 2(2) | 1(1) | 1(2) |
| 2(1) | 2(2) | 3 | 1(1) | 1(2) |
| 1(1) | 2(1) | 2(2) | 3 | 1(2) |
| 1(1) | 1(2) | 2(1) | 2(2) | 3 |
可見在經過插入排序后,相同元素的相對前后位置沒有發生改變 ,因此排序是穩定的。?
選擇排序
選擇排序的思路:分為有序區和無序區,每次將無序區的最小元素放在無序區的第一個位置,期間會發生元素的交換
# 選擇排序,復雜度為O(n^2),思路是遍歷一趟元素后,選擇最小的值放在無序區的第一位
def select_sorted(li:list)->list:for i in range(len(li)):min_loc = i# 初始化最小值的位置為第一個for j in range(i+1,len(li)-1):if li[j]<li[min_loc]:li[j],li[min_loc] = li[min_loc],li[j]# 交換元素return li?第一趟
| 3 | 2(1) | 2(2) | 1(1) | 1(2) |
|---|---|---|---|---|
| 2(1) | 3 | 2(2) | 1(1) | 1(2) |
| 2(1) | 3 | 2(2) | 1(1) | 1(2) |
| 1(1) | 3 | 2(2) | 2(1) | 1(2) |
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
?在第一趟的選擇排序種,我們可以看到相同元素2(1)和2(2)的相對位置在排序前后發生了變化,因此是不穩定排序。
其他經典的排序方法
快速排序
快排的思路:先取序列首元素作為基準值,將序列中小于基準值的元素放在左邊,大于基準值的元素放在右邊(相等的元素放在任一邊均可)。然后以該基準值作為邊界,對左右子序列遞歸進行快速排序即可實現排序
具體步驟:
1)選擇序列首元素作為基準值,左指針指向序列首位,右指針指向序列尾部;
2)若右指針的元素值大于基準值,右指針繼續左移;否則將右指針指向的元素賦值給左指針;
3)賦值完后,移動左指針,若左指針的元素小于基準值,左指針右移,否則將左指針指向的元素賦值給右指針處;
4)重復2)3)直到左右指針重合,將基準值賦值給重合的位置;
5)對左右子序列遞歸使用1)-4)步驟,這樣就實現了對序列的快速排序,遞歸終止條件為序列含有1個元素,即left<right這里保證有兩個元素的時候進行遞歸,否則退出
def partition(li:list,left:int,right:int)->int:'''這是根據路飛商城的思路來的將p元素歸位的函數:取第一個元素為p元素,移動right,若right指針的值大于P,則right繼續往左移動,否則停止移動,將值賦值給left所在的位置;然后再移動left,若left指針的值小于P,則left繼續往右移動,否則停止移動,將值賦值給right所在的位置;如此交替移動,直到left=right時,停止,并將P值賦值給left(right):param li: 需要歸位的列表:param left: 列表左指針索引,初始值為0:param right: 列表右指針索引,初始值為len(li)-1:return: 返回p歸位的索引'''#得到要歸位的元素(第一個元素)p = li[left]#當列表有兩個元素時,才進行排序while left < right:# 保證有兩個元素#這里我們從列表的右邊開始進行元素的比較while left < right and p < li[right]: # 至少兩個元素并且p元素值小于等于right指針指向的值時,右指針左移right -= 1 # right 左移一步li[left] = li[right] # 不滿足上述循環條件時,停止移動right,并且將right上的值賦值給left#右指針停止移動后,開始進行左指針的移動while left < right and p > li[left]:left += 1li[right] = li[left]#當left = right時,說明已經歸位了,將p賦值給歸位位置li[left] = preturn leftdef quickSorted(li,left,right):'''對列表進行快排:param li: 需要排序的列表:param left: 左索引:param right: 右索引:return: 返回排好序的列表'''if left < right:mid = partition(li, left, right) # 首先得到第一個歸位索引# 對左邊列表進行排序quickSorted(li,left,mid-1)# 對右邊列表進行排序quickSorted(li,mid + 1,right)?第一趟
基準值p = 5
| 5 | 4(1) | 9 | 4(2) | 8 |
|---|---|---|---|---|
| 5 | 4(1) | 9 | 4(2) | 8 |
| 4(2) | 4(1) | 9 | 4(2) | 8 |
| 4(2) | 4(1) | 9 | 9 | 8 |
| 4(2) | 4(1) | 5 | 9 | 8 |
?由上面可以看出,在進行一趟排序后,兩個4的相對位置發生了改變,因此快速排序是不穩定的
?。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
堆排序
堆排序是利用了二叉樹的數據結構來實現的,穩定排序
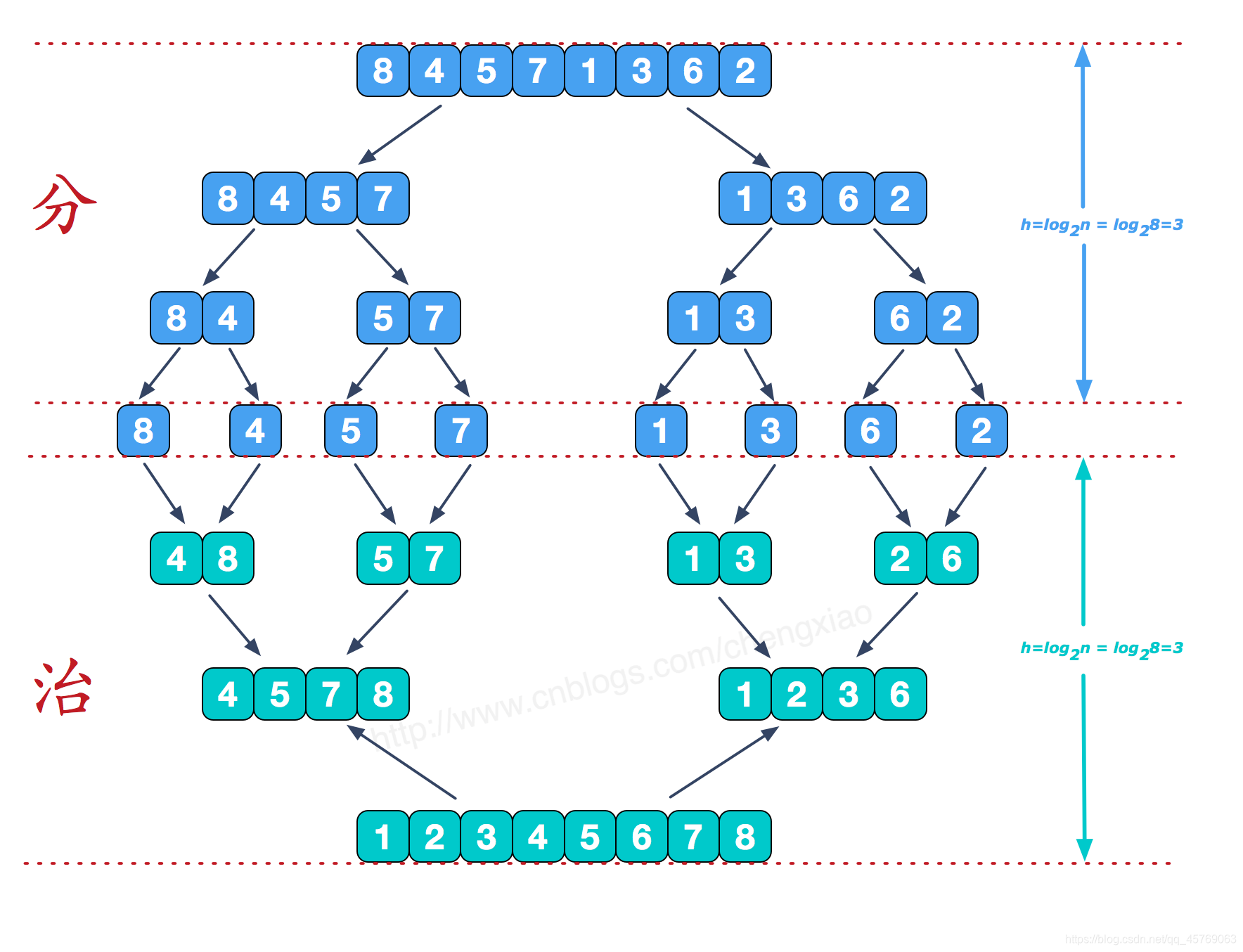
歸并排序
歸并排序的思路:將兩個有序序列利用雙指針進行合并
難點:如何將待排序的序列變成兩個有序序列,當元素只有一個的時候序列是有序的,這個是比較容易理解的。因此這里利用遞歸的方式,先將列表拆成一個個單元素列表,然后再一個個元素(有序序列)合并,回溯即可實現排序
'''
歸并排序的主要思路:將兩個有序的子列表歸并為一個有序的大列表
'''#歸并函數,假設li是由左右兩個有序的子列表組成,假設兩個子列表都是從小到大排好序的列表
def merge(li,low,mid,high):''':param li: 由左右兩個有序的子列表組成的大列表:param low: 列表的起始索引:param mid: 兩個子列表的分解處的索引,這里取前面子列表的最后一個元素的索引為mid:param high: 大列表最后一個索引:return: 從小到大排序的列表'''# 當列表中有兩個元素時進行歸并操作i = low # 第一個子列表的起始索引j = mid + 1 # 第二個子列表的起始索引比較好了的元素lTmp = [] # 用于保存while i <= mid and j <= high: # 當兩個子列表都沒有遍歷完時if li[i] > li[j]:lTmp.append(li[j])j += 1else:lTmp.append(li[i])i += 1while i <= mid:# 當右列表訪問結束后,直接將左列表進行添加lTmp.append(li[i])i += 1while j <= high:lTmp.append(li[j])j += 1li[low:high+1] = lTmp#歸并排序
def mergeSorted(li,low,high):''':param li: 列表:param low: 列表起始索引:param high: 列表結束索引:return: '''if low < high: # 保證列表有兩個元素mid = (low + high)//2mergeSorted(li,low,mid) # 對左列表進行排序mergeSorted(li,mid+1,high) # 對右列表進行排序merge(li,low,mid,high) # 將排好序的兩個列表進行歸并?歸并排序是穩定排序方式,因為在進行有序列表的合并時,這里看成左右子序列的合并,只有當左序列中的元素大于右子序列的元素的時候,才會將右子序列的元素添加到列表中,這也就保證了在左右序列中有相等元素時,會先將左序列的元素存放在列表中,然后再將右序列的元素存放在列表中
?希爾排序
希爾排序思路:希爾排序的思路其實和歸并排序是類似的,都是利用分治的方法實現,不同的是歸并排序是另開一個數組來合并兩個有序的序列進而實現序列的排序;而希爾排序則是利用插入的方式將兩個子序列合并在一起,在序列原地進行修改。
'''
希爾排序:將列表分成多組,對每一組進行插入排序,最后合并在一起,d1=len//2,di=d(i-1)//2,直到di=1,退出
'''def insert_sorted_shell(li:list,gap:int)->list:''':param li: 列表:param gap: 分組的組數和每個元素在大列表中的間隔:return: '''for i in range(gap,len(li)):# 趟數,也就是抽牌的順序,從第一張牌開始抽tmp = li[i]j = i - gap# 左邊元素while j >= 0 and li[i] < li[j]:# 若抽取的元素小于鄰近左邊的元素,則將左邊元素右移一格li[j+gap] = li[j]j -= gap# 這時候的j已經不滿足上述條件了,因此這個j位置上的元素沒有移動,而j+1上位置的元素移動了是空的li[j+gap] = tmpreturn lidef shellSorted(li):n = len(li)d = n//2while d >= 1:insert_sorted_shell(li,d)d //= 2注意:快速排序、歸并排序的左右索引都是閉區間
?不同排序方法的各維度對比
| 排序方法 | 冒泡排序 | 插入排序 | 選擇排序 | 快速排序 | 歸并排序 | 希爾排序 |
|---|---|---|---|---|---|---|
| 穩定性 | 穩定 | 穩定 | 不穩定 | 不穩定 | 穩定 | 穩定 |
| 時間復雜度 | O(n^2) | O(n^2) | O(n^2) | O(nlgn) | O(nlogn) | O(n^(3/2) ) |
| 空間復雜度 | O(1) | O(1) | O(1) | O(1) | O(n) | O(1) |
從時間復雜度(性能)上來說,一般選擇快速排序,是一種排序比較快的排序方法
從穩定性來說,一般選擇的是歸并排序





)











——Python)

)