四、極大似然參數估計
? ? ? ? ?此篇博文,玉米將和大家分享一下“張氏標定”除幾何推導外的另外一大精髓:參數估計。
? ? ? ? ?張教授在大作“A Flexible New Technique for Camera Calibration”中的原話如下:” The above solution is obtained through minimizing an algebraic distancewhich is not physically meaningful. We can refine it through maximum likelihoodinference”.意思是:上面的幾何推導僅僅是純代數上的擬合,沒有物理意義。下面讓我們通過極大似然理論對得到的結果進行改善。
?????? 順著張教授的意思,玉米先在這里為大家從概念上講述一下極大似然估計。
?????? 極大似然估計是一種估計總體未知參數的方法。它主要用于點估計問題。所謂點估計是指用一個估計量的觀測值來估計未知參數的真值。說穿了就一句話:就是在參數空間中選取使得樣本取得觀測值的概率最大的參數。
?????? 我們定義似然函數:
? ? ? ?總體分布為離散型的:(p是已知的分布律)
?
? ? ? ? 總體分布為連續性的:(f為概率密度函數)
? ? ? ? 極大似然法就是在的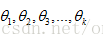
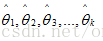
? ? ? ? ?如果在內: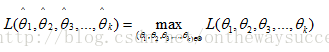
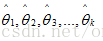
? ? ? ? ? ??列了這么一大圈兒概念,估計大家看的都昏昏入睡了。玉米在這里用通俗點兒的方式解釋一下極大似然估計:
? ? ? ? 對很多實驗,我們可以觀察到樣本,但影響樣本的參數卻是未知的。那我們就得對樣本進行估計。既然我們要去估計,那么就想要估計的準。極大似然法就只在概率分布的觀念下,指導我們估計的更準的方法。現實世界中,存在著一條普遍規律:與現實相差越遠的概率越小。這就相當于人群中,非主流總是比主流要少一樣,偏差大的總是占少數。所以,可能發生的概率越大就會越接近真實值。極大似然法就是應用這種思想,認為可能性最大的就是最優的估計值。即極大似然估計值就是最接近真實值的參數值。
? ? ? ? ? 那么,極大似然為什么有這么一個別致的名字呢?什么是似然呢?是因為估計值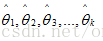 不是隨機變量,所以不能把它的可能性稱為概率,那么數學家們就想了這樣(likelihood)一個名字來代表可能性。
不是隨機變量,所以不能把它的可能性稱為概率,那么數學家們就想了這樣(likelihood)一個名字來代表可能性。
?????? 極大似然法的一些概念上的問題玉米就講到這里了。下面然玉米帶這大家分析一個具體問題:張教授在張氏標定法中所用的極大似然估計。
?????? 首先來看一下,為什么標定的內外參數可以用極大似然法進行估計:
?????? 因為我們是假定圖像上的角點是被噪聲干擾的,且我們認為這些噪聲是高斯噪聲。那么對于噪聲的幅度就是給觀測值造成的誤差。但高斯噪聲的概率密度我們是已知的,所以我們可以用前面所述的極大似然估計的思想去“猜”真值。
?????? 那么接下來我們就需要構造一個似然函數,然后尋找其最大值了。張教授在文章中直接略過推導,直接給出了公式:
? ? ? ? ?說當此式取得最小值時,就是參數的最大似然估計值。
?????? 玉米在這里為大家講一下自己的理解:
?????? 設,角點附近的噪聲服從高斯分布
?????? 則:角點mij的樣本值服從如下,概率密度函數:
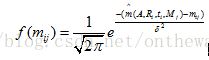
? ? ? ?現在構造,似然函數:
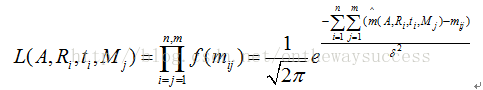
? ? ? ? 現在讓L取得最大值,則可令下式最小:
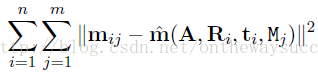
? ? ? ? 那么怎么令上面這個目標函數達到最小值呢,張氏標定法運用了可以用來解決多參數非線性系統優化問題的Levenberg-Marquardt算法。對于該方法,詳細的介紹大家可以參照《The levenberg-marquardt algorithm, implementation andtheory》一文進行深入了解。這里給出下載本文的鏈接:
http://link.springer.com/chapter/10.1007%2FBFb0067700
? ? ? ? ?那么張氏標定法在不考慮鏡頭畸變的情況下的,獲取攝像機內外參數的數理推導過程。玉米就為大家講到這里了。下面一篇博文,玉米會給大家分析一下,張氏標定法是怎樣分析攝像機的非線性畸變的。
?
還是老話:玉米才疏學淺,講解之中難免有紕漏,請大家諒解,并指正。
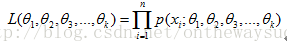
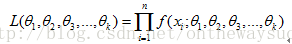
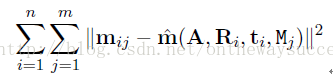







:解碼)



——重排序)
![《MySQL必知必會》[01] 基本查詢](http://pic.xiahunao.cn/《MySQL必知必會》[01] 基本查詢)
立體標定與立體校正 【計算機視覺學習筆記--雙目視覺幾何框架系列】)





