五、畸變矯正—讓世界不在扭曲
? ? ? ? ? 這篇博文所要講述的內容,是標定的主要用途之一:矯正攝像機的畸變。對于圖像畸變矯正的方法,張正友教授也在其大作“A Flexible New Technique forCamera Calibration”中給出。
? ? ? ? ?玉米在這里先為大家介紹一下,攝像機畸變主要有哪幾種以及這些討厭的畸變從何而來。
攝像機畸變主要包含:鏡像畸變、切向畸變。玉米在這里分別講述一下,并引用一些圖片,使大家對他們有一個直觀的認識。
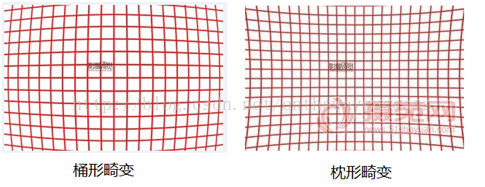
? ? ? ? ?1.徑向畸變:產生原因是光線在遠離透鏡中心的地方比靠近中心的地方更加彎曲徑向畸變主要包含桶形畸變和枕形畸變兩種。下面兩幅圖是這兩種畸變的示意:
? ? ? ? ? 它們在真實照片中是這樣的:

? ? ? ? ? ?2.切向畸變:產生的原因透鏡不完全平行于圖像平面,這種現象發生于成像儀被粘貼在攝像機的時候。下面圖片來自于《學習opencv》p413。
? ? ? ? ? 畸變矯正,首先應該知道畸變系數,然后做與畸變相反的變換,消除畸變。
? ? ? ? ? 張氏標定法中只關注徑向畸變。我們是按照張氏標定,計算畸變系數的。那么,下面讓我們來看一下徑向畸變的數學表達。
? ? ? ? ? 因為在實際情況下,徑向畸變較小,所以其可以用主點(principle point)周圍的泰勒級數展開的前幾項進行描述。張氏標定法,利用前兩項來確定徑向畸變的畸變系數。數學表達式如下:
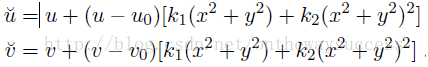
其中,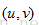
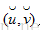
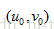
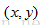
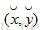
???????? 那么對于圖像上的任意一點,我們有兩個個等式。化成矩陣形式:
? ? ? ? 通過前面兩篇博文所介紹的內容,求得的攝像機模型,我們可以計算出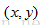
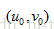
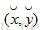
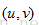
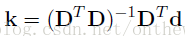
其中,D等式左邊的方程的系數矩陣,d是等式右邊的有畸變的像素坐標與無像素坐標之差構成的矩陣。有上式,一步到位,計算出畸變系數。
?????? 但是,但是,大家先別急。我們的參數求解之路還沒有結束。為了使標定得到的估算實際的、存在徑向畸變的攝像機參數。我們需要把,剛剛求解得到的畸變參數,連同前面得到的理想無畸變條件下的內外參數一起,進行極大似然估計。
?????? 這里的極大似然估計方法與上一篇博文《極大似然參數估計》相同,玉米在這里就不在贅述。
依然是以最小化下列函數為目標,只不過此次參數估計中又多加了k1,k2:
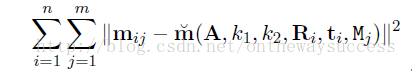
? ? ? ? 然后,仍然用Levenberg-Marquardt算法進行計算。最終就得到了,我們想要在考慮畸變情況下,攝像機的參數。
張氏標定,大功告成!
? ? ? ?下面讓我們矯正畸變:? ? ? ? 就是這樣一個簡單的公式,就完成了畸變矯正。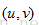
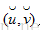
? ? ? ? 最后給大家展示兩幅圖,讓大家看一下畸變矯正的成果:
? ? ? ? ? 這就是張氏標定帶給我們的第一個直觀的好處,后面還有兩個大好處,玉米將為您介紹。
? ? ? ? ? 玉米才疏學淺,懇請請大家批評指正!
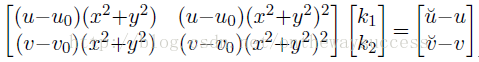
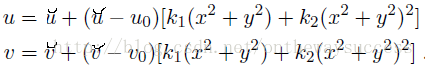



——重排序)
![《MySQL必知必會》[01] 基本查詢](http://pic.xiahunao.cn/《MySQL必知必會》[01] 基本查詢)
立體標定與立體校正 【計算機視覺學習筆記--雙目視覺幾何框架系列】)














![BZOJ 1937: [Shoi2004]Mst 最小生成樹 [二分圖最大權匹配]](http://pic.xiahunao.cn/BZOJ 1937: [Shoi2004]Mst 最小生成樹 [二分圖最大權匹配])