繼續!!!!!!
一、四個坐標系簡介和轉換
相機模型為以后一切標定算法的關鍵,只有這邊有相當透徹的理解,對以后的標定算法才能有更好的理解。本人研究了好長時間,幾乎每天都重復看幾遍,最終才會明白其推導過程。
? ? ?我覺得首先我們要理解相機模型中的四個平面坐標系的關系:像素平面坐標系(u,v)、像平面坐標系(圖像物理坐標第(x,y)、相機坐標系(Xc,Yc,Zc)和世界坐標系(Xw,Yw,Zw),在每一篇介紹相機模型的文章中都有介紹。
? ? ?我剛開始理解時,看著那一堆的公式十分的頭暈,我相信很多初學者和我一樣,但仔細想想,只不過是,我們假設了一些參數,使四個坐標系之間的坐標聯系起來,這樣我們就可以從拍攝的圖片上一個點坐標一路反推出世界中的那個點的坐標,這樣就達到了我們的目的,三維重建。而那些我們假設的參數,就是我們要標定的內外參數。

?
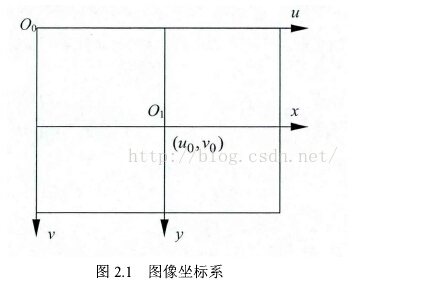
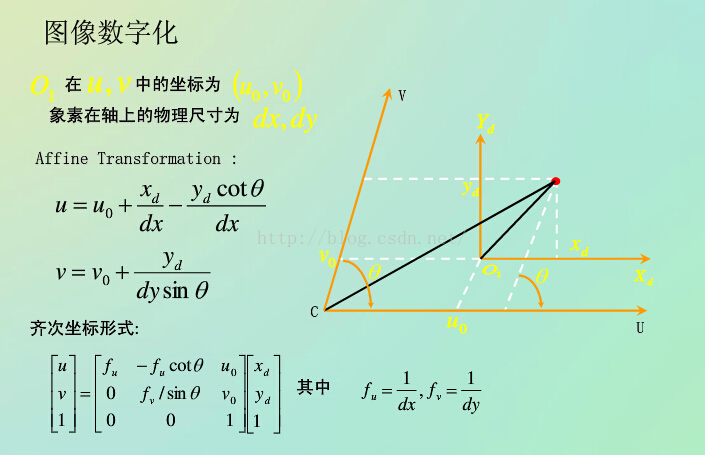
1、像素坐標與像平面坐標系之間的關系?
? ? ? 確定他們的關系之前,我們可以假設每一個像素在u軸和v軸方向上的物理尺寸為dx和dy。仔細看下他們的模型可以推出以下公式(這個還是比較好理解的):
?
?
?

?
解釋:1、dx,dy,u0,v0其實都是我們假設出來的參數,dxdy表示感光芯片上像素的實際大小,是連接像素坐標系和真實尺寸坐標系的,u0,v0是圖像平面中心,最終是要我們求的內外參數。
得出這個公式后我們可以運用線性代數的知識把方程用矩陣形式表示:

當然我們也可以用另一種矩陣形式表示:

2、相機坐標系與世界坐標系之間的關系?
? ? ?這兩個坐標系之間的關系我們可以旋轉矩陣R和平移矩陣T來得到以下關系:
?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 公式4
? ?解釋:1、 在這個公式中,R為3*3矩陣,T為3*1,0為(0,0,0),簡化用Lw表示后為4*4矩陣。
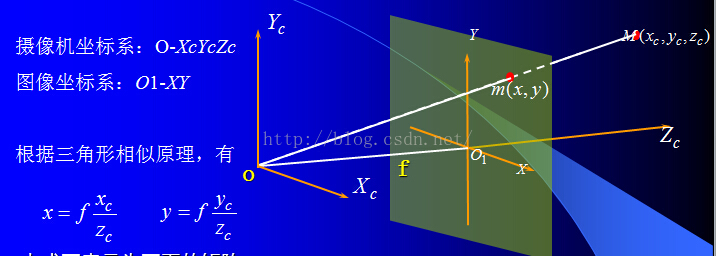
3、成像投影關系(相機坐標系與像平面坐標系)?
? ? ?在相機模型中我們可以得到以下公式:
?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?公式5
? ? ? ? ? ?解釋:1、
同樣我們用矩陣形式表示:
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?公式6
?
4、得到公式
?
而我們可以將以上公式綜合一下就可以得到:
??

因此,內參數矩陣可以表示為:

?
外參矩陣可以表示為:
?
當然在好多資料上都有這種做法:
上圖中表示的情況是像素坐標系和圖像物理坐標系的兩個坐標軸不是平行的關系,像素坐標系的兩個坐標軸也不是垂直90°的關系,而圖像物理坐標系的兩個坐標軸是垂直關系。所以,我們在轉換兩個坐標軸的坐標之間的關系時就必須考慮像素坐標系兩個坐標軸之間的夾角了。就有了上面的不同的內參矩陣,理解了就好了。
?
二、圖像坐標:我想和世界坐標談談(B)
? ? ? ? ?玉米將在這篇博文中,對圖像坐標與世界坐標的這場對話中涉及的第二個問題:談話方式,進行總結。世界坐標是怎樣變換進攝像機,投影成圖像坐標的呢?
? ? ? ? 玉米做了一個簡單的圖示,在這里做一個提綱。圖中顯示,世界坐標系通過剛體變換到達攝像機坐標系,然后攝像機坐標系通過透視投影變換到達圖像坐標系。可以看出,世界坐標與圖像坐標的關系建立在剛體變換和透視投影變換的基礎上。為了獎勵剛體變和透視投影變換溝通了“世界上最遠的距離”,玉米在圖上獎勵了他們兩朵小紅花。哈哈
?
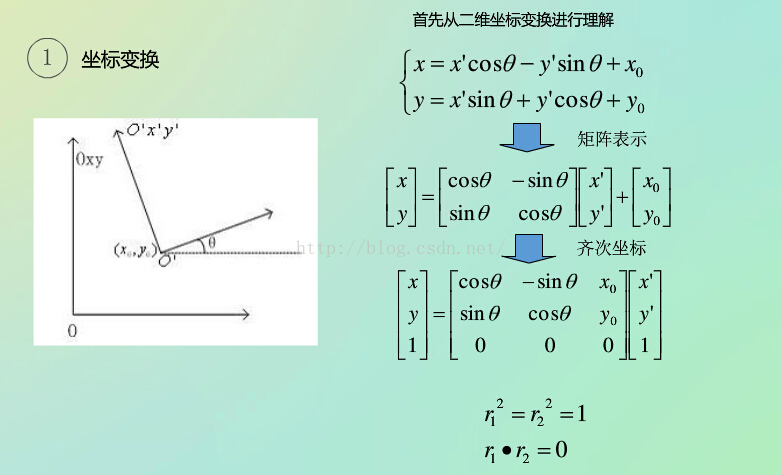
?首先,讓我們來看一下剛體變換是如何將世界坐標系與圖像坐標系聯系起來的吧。這里,先對剛體變換做一個介紹:
? ? ? ? 剛體變換(regidbody motion):三維空間中, 當物體不發生形變時,對一個幾何物體作旋轉,?平移的運動,稱之為剛體變換。
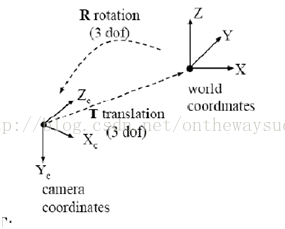
因為世界坐標系和攝像機坐標都是右手坐標系,所以其不會發生形變。我們想把世界坐標系下的坐標轉換到攝像機坐標下的坐標,如下圖所示,可以通過剛體變換的方式。空間中一個坐標系,總可以通過剛體變換轉換到另外一個個坐標系的。轉一轉,走一走,就到另外一個坐標系下了。以前可能是面朝大海,經過平移旋轉,最終可能只能面朝冰山了,哈哈
下面讓我來看一下,二者之間剛體變化的數學表達。
?
其中,XC代表攝像機坐標系,X代表世界坐標系。R代表旋轉,T代表平移。R、T與攝像機無關,所以稱這兩個參數為攝像機的外參數(extrinsic parameter)可以理解為兩個坐標原點之間的距離,因其受x,y,z三個方向上的分量共同控制,所以其具有三個自由度。
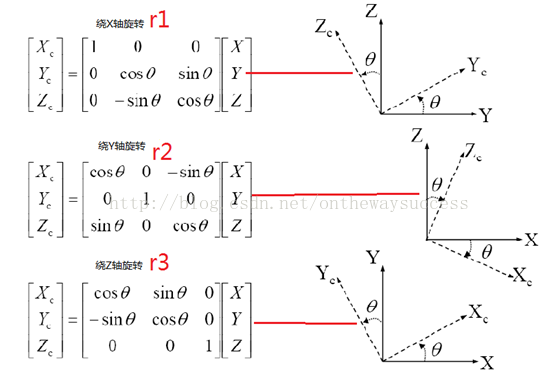
? ? ? ? ?R則為分別繞XYZ三軸旋轉的效果之和。如下面所示:
?
?R=r1*r2*r3.其由三個方向的θ控制,故具有三個自由度。
? ? ? ? ? ?好了,剛體變換就講完了。大家應該都了解,世界坐標系到攝像機坐標系之間的轉換過程了吧。
? ? ? ? ? 接下來,讓我們看看攝像機坐標下的坐標如何投影到圖像坐標系下,最終變為照片中的一個像素。這其中包含兩個過程:一是從攝像機坐標到“空間圖像坐標”(x,y)所發生的透視投影;二是從“連續圖像坐標”到“離散圖像坐標”(u,v)。后者我們已經在第一篇博文中解釋過。所以在這里,主要介紹一下透視投影。
? ? ? ? ?透視投影(perspective projection):?用中心投影法將形體投射到投影面上,從而獲得的一種較為接近視覺效果的單面投影圖。有一點像皮影戲。它符合人們心理習慣,即離視點近的物體大,離視點遠的物體小,不平行于成像平面的平行線會相交于消隱點(vanish point)。
? ? ? ? ?啰嗦這么多,其實大家看看示意圖,看看公式,秒懂。
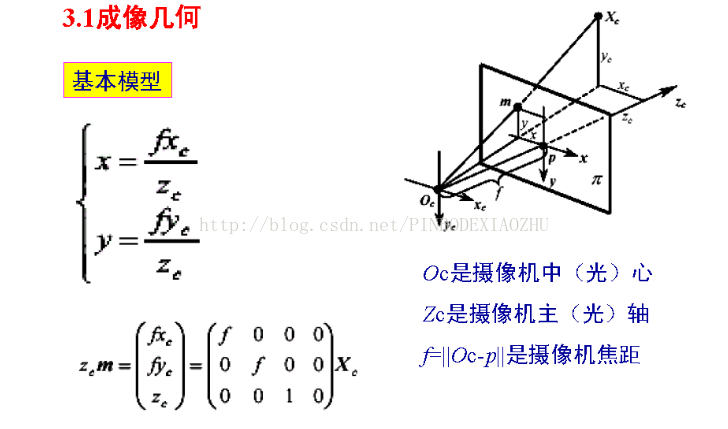
??以圖中B(XB,YB)點為例,在小孔成像攝像機模型下(幾何分析的最常用模型)。這里的f為攝像機的焦距,其屬于攝像機的內參數(intrinsic parameter)。其在成像平面上的投影點b(xb,yb)的坐標利用簡單的相似三角形比例關系很容易求出:
?
上面兩式也闡明了攝像機坐標與圖像坐標之間的透視投影關系。
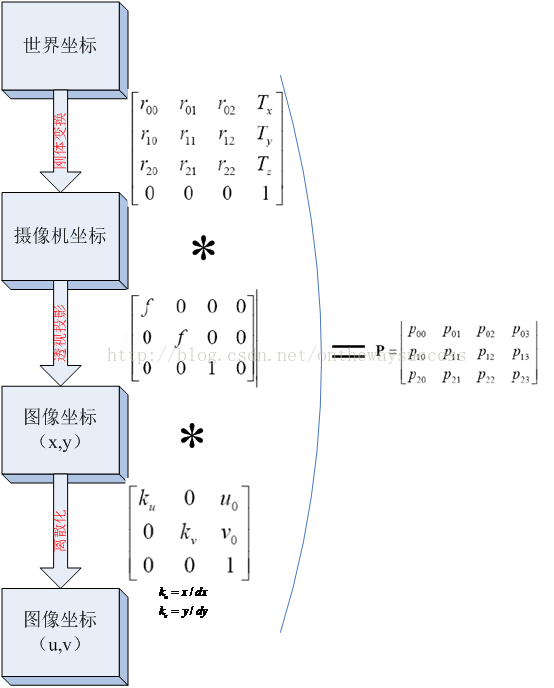
? ? ? ? ? ? 好吧,現在玉米已經把圖像坐標與世界坐標之間的這場對話所需經歷的三個波折的過程加以了解釋。即:剛體變換、透視投影、(x,y)換(u,v)(ps.這個在上一篇博文中講過)。接下來玉米用一張圖把三個過程連接起來。實現從世界坐標(X,Y,Z)到(u,v)之間的轉換。讓圖像坐標與世界坐標直接對話。
? ? ? ? ?下圖中的轉換關系,都是用齊次坐標表達的,大家會發現這樣的表達非常整潔。
? ? ? ? ?其實這張圖顯示的過程還有一個名字:攝像機模型(camera model)。其實也就是攝像機的幾何模型了。
? ? ? ? ?將三者相乘,可以把這三個過程和在一起,寫成一個矩陣:
P就是世界坐標到圖像坐標的直接聯系人,P就表示了一個投影相機,有下面公式:
注意在表示齊次坐標時,需要在符號上面加個小帽子。除去齊次坐標控制位P23,P具有11個自由度。
?? ? ? 攝像機模型及其中涉及的坐標系等,是弄清3D重建幾何框架的基礎。可以把它們視為基本運算關系。后面對于三維重建幾何框架的推導,都是要用到三個基本坐標系和攝像機模型的。
轉:https://blog.csdn.net/messi_cyc/article/details/78052931


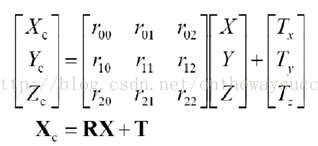
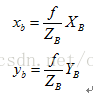
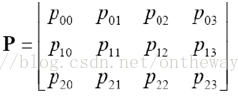
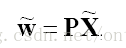





)




------內部指令)
![【bzoj3555】[Ctsc2014]企鵝QQ 簡單哈希](http://pic.xiahunao.cn/【bzoj3555】[Ctsc2014]企鵝QQ 簡單哈希)
函數定義及用法畸變矯正與立體校正)
- 內含紅黑樹分析全過程)
)


——觀察者設計模式)

