關卡名	理解與貪心有關的高頻問題	我會了??
內容	1.理解跳躍游戲問題如何判斷是否能到達終點	??
	2.如果能到終點，如何確定最少跳躍次數	??

1. 跳躍游戲?

leetCode 55 給定一個非負整數數組，你最初位于數組的第一個位置。數組中的每個元素代表你在該位置可以跳躍的最大長度，判斷你是否能夠到達最后一個位置。

示例1：

輸入: [2,3,1,1,4]

輸出: true

解釋: 從位置 0 到 1 跳 1 步, 然后跳 3 步到達最后一個位置。

示例2：

輸入: [3,2,1,0,4]

輸出: false

解釋: 無論怎樣，你總會到達索引為 3 的位置。但該位置的最大跳躍長度是 0 ，所以你永遠不可能到達最后一個位置。

如果當前位置元素如果是3，我究竟是跳幾步呢，一步，兩步，還是三步？這里的關鍵是判斷能否到達終點，不用每一步跳躍到哪個位置，而是盡可能的跳躍到最遠的位置，看最多能覆蓋到哪里，只要不斷更新能覆蓋的距離，最后能覆蓋到末尾就行了。

?

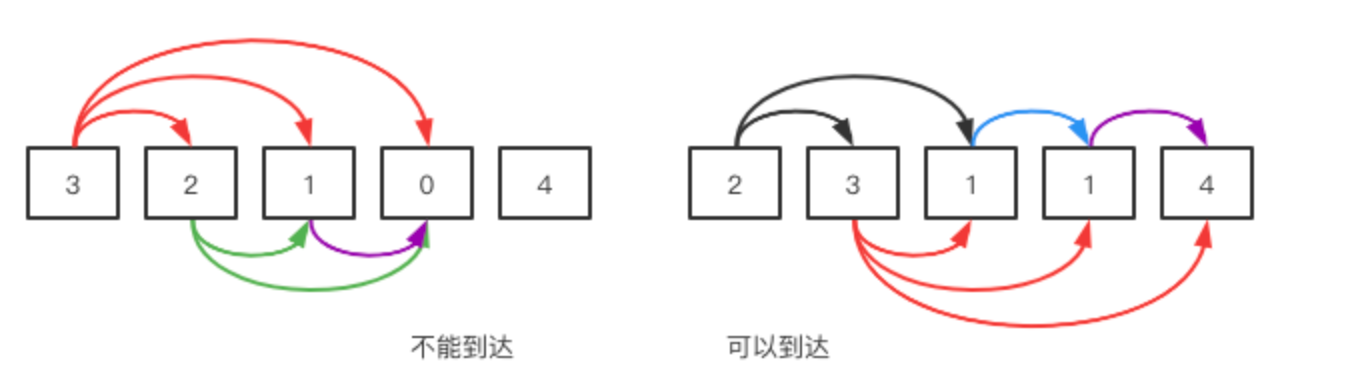
例如上面的第一個例子，3能覆蓋的范圍是后面的{2,1,0}，2接下來能覆蓋后面的{1,0},而1只能覆蓋到{0}，所以無法到達4。
而第二組序列，2能覆蓋{3,1}，3可以覆蓋后面的{1,1,4},已經找到一條路了。1只能到下一個1，下一個1能到4，所以這里有{2,1,1,4}和{2,3,1,1,4}兩種走法，加起來有3種跳法。
我們可以定義一個cover表示最遠能夠到達的方位，也就是i每次移動只能在其cover的范圍內移動，每移動一次，cover得到該元素數值（新的覆蓋范圍）的補充，讓i繼續移動下去。而cover每次按照下面的結果判斷。如果cover大于等于了終點下標，直接return true就可以了：
cover= max(該元素數值補充后的范圍, cover本身范圍)
針對上圖的兩個序列再解釋一下：
1.在第二個圖中，第一個元素，nums[0]=2，此時conver=2能覆蓋到{3,1}兩個元素。
2.繼續，第二個元素nums[1]=3，此時能繼續覆蓋的范圍就是1+3，能覆蓋{1，1，4}三個位置。此時cover=2，而”該元素數值補充后的范圍“是1+3=4，所以新的conver=max{4,2}，此時就是cover>=nums.length-1。
其他情況都可以使用類似的方式來判斷 ，所以代碼就是：

public boolean canJump(int[] nums) {if (nums.length == 1) {return true;}//覆蓋范圍, 初始覆蓋范圍應該是0，因為下面的迭代是從下標0開始的int cover = 0;//在覆蓋范圍內更新最大的覆蓋范圍for (int i = 0; i <= cover; i++) {cover = Math.max(cover, i + nums[i]);if (cover >= nums.length - 1) {return true;}}return false;
}

這道題目的難點是要想到覆蓋范圍，而不用拘泥于每次究竟跳幾步，覆蓋范圍是可以逐步擴展的，只有能覆蓋就一定是可以跳過來的，不用管是怎么跳的。

2 最短跳躍游戲

在上題再進一步，假設一定能到達末尾，然后讓你求最少到達的步數該怎么辦呢？這就是LeetCode45上面的例子。可以看到，有三種走法{2,3,4}、{2,1,1,4}和{2,3,1,1,4}，那這時候該怎么辦呢？
具體該怎么實現呢？網上有很多解釋，代碼也基本雷同，而且也很明顯是將上一題的代碼修改了一下，但是難在不好理解，我現在給一個比較好理解的方式：貪心+雙指針。
我們重新觀察一下結構圖，為了便于分析，我們修改一下元素序列，我們需要四個變量：

• left用來一步步遍歷數組
• steps用來記錄到達當前位置的最少步數
• right表示當前步數下能夠覆蓋到的最大范圍
• 我們還需要一個臨時變量conver，假如left到達right時才更新right

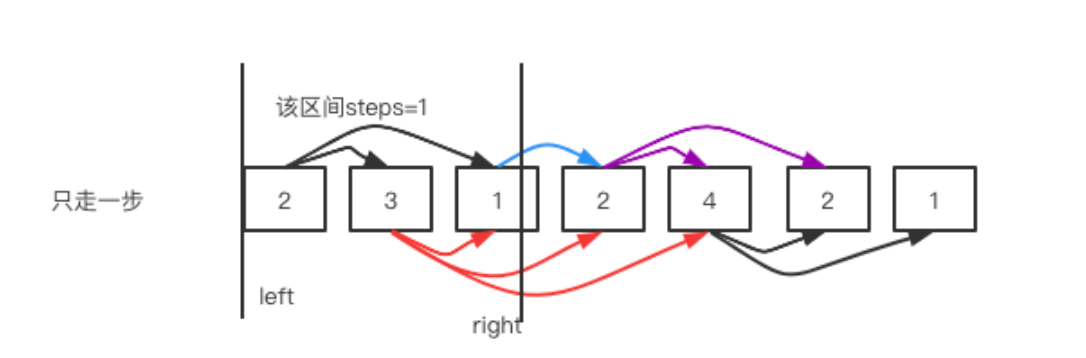在這個圖中，開始的元素是 2，如果只走一步，step=1，可跳的范圍是{3,1}。也就是如果只走一步，最遠只能到達1，此時conver=nums[0]=2，因此我們用right=nums[2]來保存這個位置，這表示的就是走一步最遠只能到nums[2]。
接下來，我們必須再走一步，step=2，如下圖，此時可選元素是{3,1}， 3能讓我們到達的距離是left+nums[left]=1+3=4，而1能讓我們到達的位置是left+nums[left]=2+1=3，而所以我們獲得最遠覆蓋距離conver=4 。

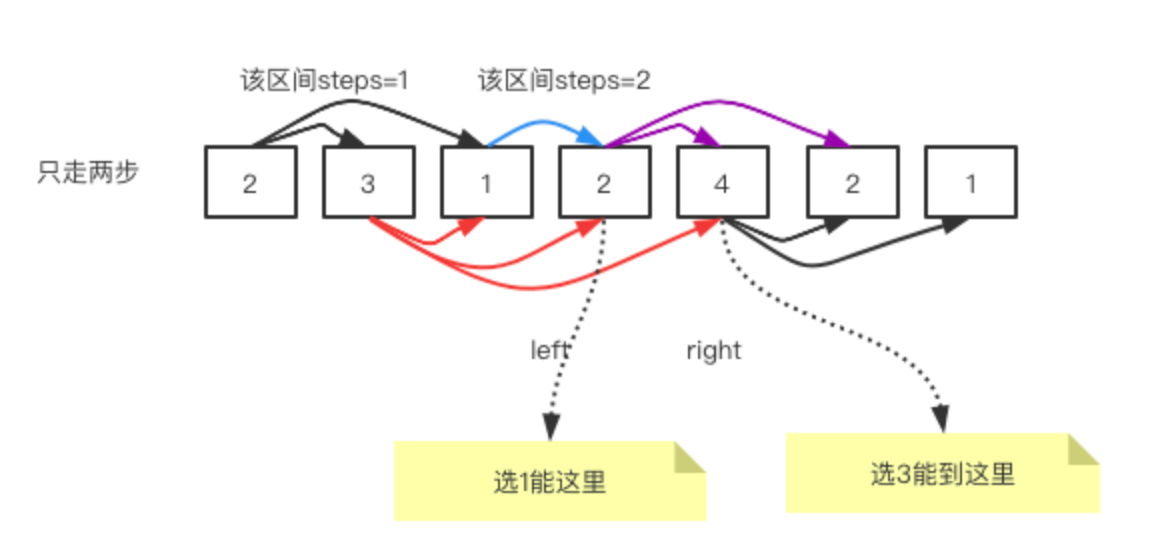然后用left和right將step=2的范圍標記一下：

?此時還沒有到終點，我們要繼續走，在這里我們可選擇的元素是{2,4}，如果選擇2，則可以到達left+nums[left]=3+2=5,如果選擇4則是left+nums[left]=4+4=8，已經超越邊界了，所以此時一定將末尾覆蓋了。

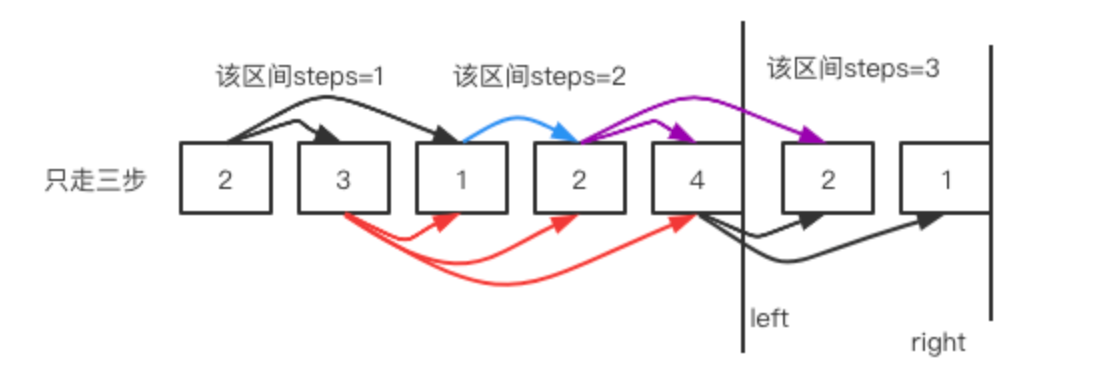
這樣我們就知道最少需要走3次。
這個過程怎么用代碼表示呢？看代碼：

public int jump(int[] nums) {int right = 0;int maxPosition = 0;int steps = 0;for(int left=0;i<nums.length;left++){//找能跳的最遠的maxPosition = Math.max(maxPosition,nums[left]+left);if(left==right){ //遇到邊界，就更新邊界，并且步數加一right = maxPosition;steps++;}//right指針到達末尾了。if (right >= nums.length - 1) {return steps;}}return steps;
}