優質博文：IT-BLOG-CN
一、題目
給你一個二叉樹的根節點root，判斷其是否是一個有效的二叉搜索樹。有效 二叉搜索樹定義如下：
【1】節點的左子樹只包含 小于 當前節點的數。
【2】節點的右子樹只包含 大于 當前節點的數。
【3】所有左子樹和右子樹自身必須也是二叉搜索樹。
示例 1：
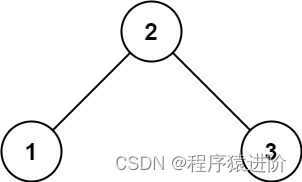
輸入：root = [2,1,3]
輸出：true
示例 2：
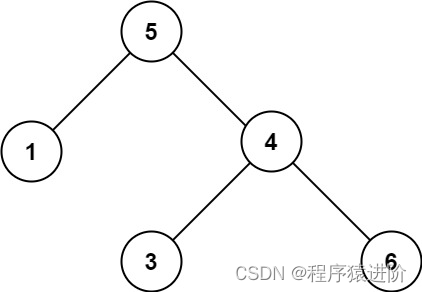
輸入：root = [5,1,4,null,null,3,6]
輸出：false
解釋：根節點的值是5，但是右子節點的值是4。
樹中節點數目范圍在
[1, 104]內
-231 <= Node.val <= 231 - 1
二、代碼
【1】遞歸： 要解決這道題首先我們要了解二叉搜索樹有什么性質可以給我們利用，由題目給出的信息我們可以知道：如果該二叉樹的左子樹不為空，則左子樹上所有節點的值均小于它的根節點的值； 若它的右子樹不空，則右子樹上所有節點的值均大于它的根節點的值；它的左右子樹也為二叉搜索樹。
這啟示我們設計一個遞歸函數helper(root, lower, upper)來遞歸判斷，函數表示考慮以root為根的子樹，判斷子樹中所有節點的值是否都在(l,r)的范圍內（注意是開區間）。如果root節點的值val不在(l,r)的范圍內說明不滿足條件直接返回，否則我們要繼續遞歸調用檢查它的左右子樹是否滿足，如果都滿足才說明這是一棵二叉搜索樹。
那么根據二叉搜索樹的性質，在遞歸調用左子樹時，我們需要把上界upper改為root.val，即調用helper(root.left, lower, root.val)，因為左子樹里所有節點的值均小于它的根節點的值。同理遞歸調用右子樹時，我們需要把下界lower改為root.val，即調用helper(root.right, root.val, upper)。
函數遞歸調用的入口為helper(root, -inf, +inf)，inf表示一個無窮大的值。
class Solution {public boolean isValidBST(TreeNode root) {return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);}public boolean isValidBST(TreeNode node, long lower, long upper) {if (node == null) {return true;}if (node.val <= lower || node.val >= upper) {return false;}return isValidBST(node.left, lower, node.val) && isValidBST(node.right, node.val, upper);}
}
時間復雜度： O(n)，其中n為二叉樹的節點個數。在遞歸調用的時候二叉樹的每個節點最多被訪問一次，因此時間復雜度為O(n)。
空間復雜度： O(n)，其中n為二叉樹的節點個數。遞歸函數在遞歸過程中需要為每一層遞歸函數分配棧空間，所以這里需要額外的空間且該空間取決于遞歸的深度，即二叉樹的高度。最壞情況下二叉樹為一條鏈，樹的高度為n，遞歸最深達到n層，故最壞情況下空間復雜度為O(n)。
【2】中序遍歷： 基于方法一中提及的性質，我們可以進一步知道二叉搜索樹「中序遍歷」得到的值構成的序列一定是升序的，這啟示我們在中序遍歷的時候實時檢查當前節點的值是否大于前一個中序遍歷到的節點的值即可。如果均大于說明這個序列是升序的，整棵樹是二叉搜索樹，否則不是，下面的代碼我們使用棧來模擬中序遍歷的過程。
可能有讀者不知道中序遍歷是什么，我們這里簡單提及。中序遍歷是二叉樹的一種遍歷方式，它先遍歷左子樹，再遍歷根節點，最后遍歷右子樹。而我們二叉搜索樹保證了左子樹的節點的值均小于根節點的值，根節點的值均小于右子樹的值，因此中序遍歷以后得到的序列一定是升序序列。
class Solution {public boolean isValidBST(TreeNode root) {Deque<TreeNode> stack = new LinkedList<TreeNode>();double inorder = -Double.MAX_VALUE;while (!stack.isEmpty() || root != null) {while (root != null) {stack.push(root);root = root.left;}root = stack.pop();// 如果中序遍歷得到的節點的值小于等于前一個 inorder，說明不是二叉搜索樹if (root.val <= inorder) {return false;}inorder = root.val;root = root.right;}return true;}
}
時間復雜度： O(n)，其中n為二叉樹的節點個數。二叉樹的每個節點最多被訪問一次，因此時間復雜度為O(n)。
空間復雜度： O(n)，其中n為二叉樹的節點個數。棧最多存儲n個節點，因此需要額外的O(n)的空間。
)
