題意理解：

1. ????????每個數字在每個組合中只能使用?一次?
2. ????????數字可以重復——>難點（如何去重）
3. ????????每個組合和=target

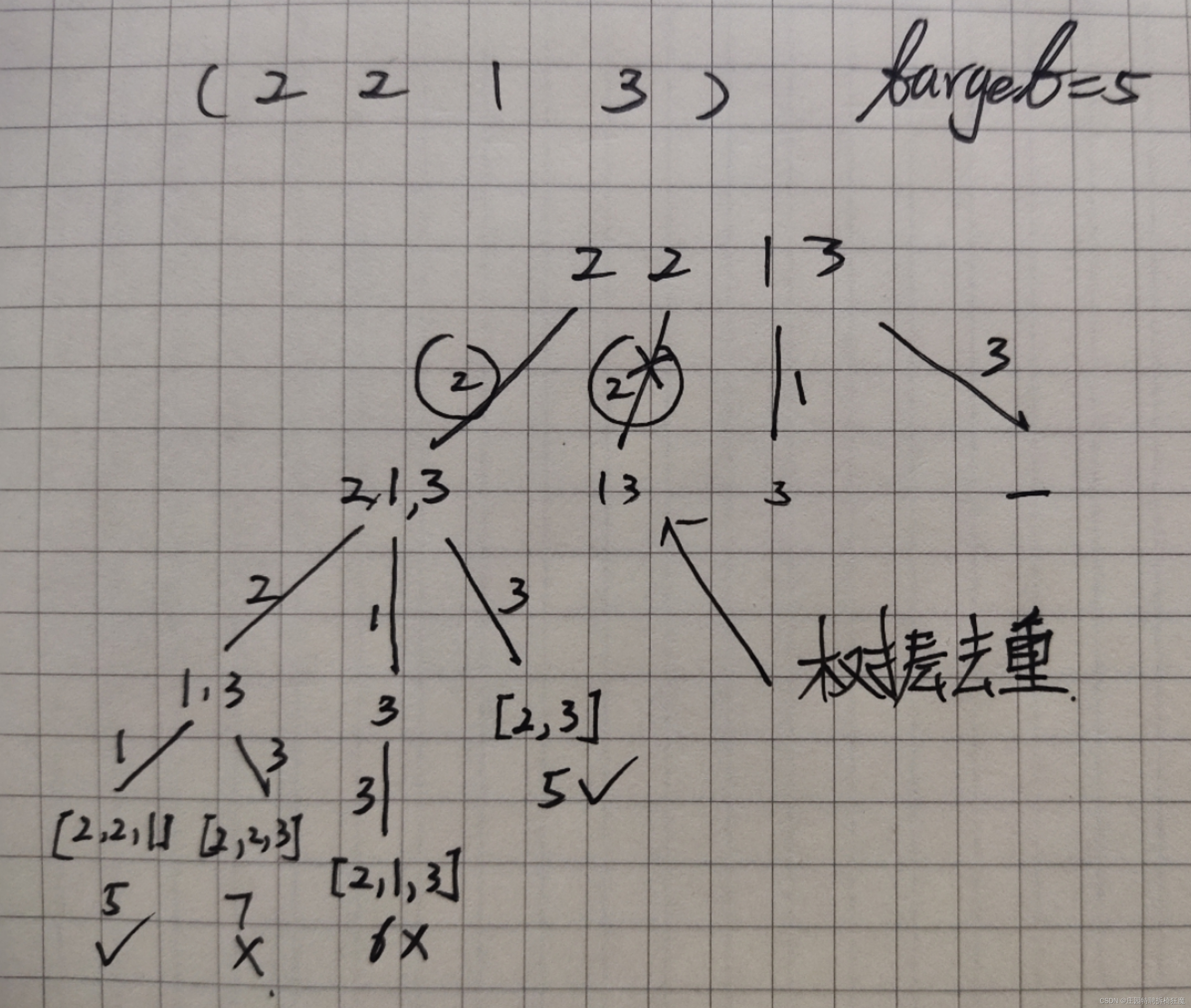
? ? ? ? 求組合，對合限制，考慮回溯的方法。——將其抽象為樹結構。

? ? ? ? 樹的寬度——分支大小

? ? ? ? 樹的深度——最長的組合（和=target）

??去重難點：

????????根據《代碼隨想錄》關于樹層去重的引入：

? ? ? ? 第一個位置選2，再次選2的話，下面的分支回出現重復的[2,3]組合。

? ? ? ? 實際上保留第一個分支，之后同一位置相同的數值選項可以剪除。

? ? ? ? 用used[]數組來維護是否被訪問的狀態。

????????

回溯的方法：

? ? ? ? 1.確定返回值+參數列表

? ? ? ? 2.確定終止條件|剪枝條件

? ? ? ? 3.單層邏輯|回溯操作

1.暴力回溯+剪枝優化

考慮返回值一般為void, 參數包含數組，和目標值，當前數值指示下標

終止條件： sum>=4,特別的sum==4時收集結果。

單層遞歸邏輯：一定要對sum和path、used數組做好回溯操作。

數層剪枝：candidates[i-1]==candidates[i]遇到重復值

? ? ? ? used[i-1]=true:表示上一個重復的值，在該組合內被用到。

? ? ? ? used[i - 1] == false：表示上一個重復值在該組合內沒有用到，應該是同一樹層用到——即數層重復，剪枝。

List<List<Integer>> result=new ArrayList<>();LinkedList<Integer> path=new LinkedList<>();int sum=0;public List<List<Integer>> combinationSum2(int[] candidates, int target) {boolean[] used=new boolean[candidates.length];Arrays.sort(candidates);Arrays.fill(used, false);backtrackig(candidates,target,0,used);return result;}public void backtrackig(int[] candidates, int target,int startIndex,boolean[] used){//終止|剪枝if(sum>target) return;else if (sum==target) {result.add(new ArrayList<>(path));return;}//單層遞歸邏輯for(int i=startIndex;i<candidates.length;i++){//數層剪枝if(i!=0&&candidates[i-1]==candidates[i]&&used[i-1]==false) continue;path.add(candidates[i]);sum+=candidates[i];used[i]=true;backtrackig(candidates,target,i+1,used);path.removeLast();sum-=candidates[i];used[i]=false;}}

注意兩個特殊的地方：

Arrays.sort(candidates);//數組排序

Arrays.fill(used, false);//數組填充，實際上該數組默認也是false.

2.分析

時間復雜度：O()

空間復雜度：O(n)