前言

計劃是通過本文的撰寫，捋清楚TSP和VRP的本質不同。(什么是本質?)

對比	TSP（旅行商問題）	VRP（車輛路徑問題）
描述	給定一個城市列表以及每對城市之間的距離，訪問每個城市一次并返回出發城市的最短路線是什么	車隊需要向給定的一組客戶家中取貨，需要遍歷的最佳路線集是什么？
輸入	城市數量，距離矩陣	城市數量，距離矩陣，任務量，卡車容量
約束	每個城市僅訪問一次	每個城市僅訪問一次，滿足容量要求
目標	最小化總旅行距離	最小化總旅行距離
輸出	一個旅行商訪問城市的順序	多個車輛的行駛路線
空間	城市序列：$(n?1)!$	城市序列加上車輛任務分配：$n!<S<P(n,m{)}^k$

以$n=13，m=5，k=3$為例，對比解空間：

• TSP解空間：$(n?1)!=(13?1)!=12!=4.79\times 10^8$
• VRP解空間：
  • 下限：$n!=13!=12!=6.23\times 10^9$
  • 上限：$P(n,m{)}^k=P(15,5{)}^3=3.68\times 10^{15}$

旅行商問題 (TSP)

問題介紹

旅行商問題（英語：Travelling salesman problem, TSP）在1930年被首次提出，是優化領域研究最深入的問題之一。問題的表述是：“給定一個城市列表以及每對城市之間的距離，訪問每個城市一次并返回出發城市的最短路線是什么？”

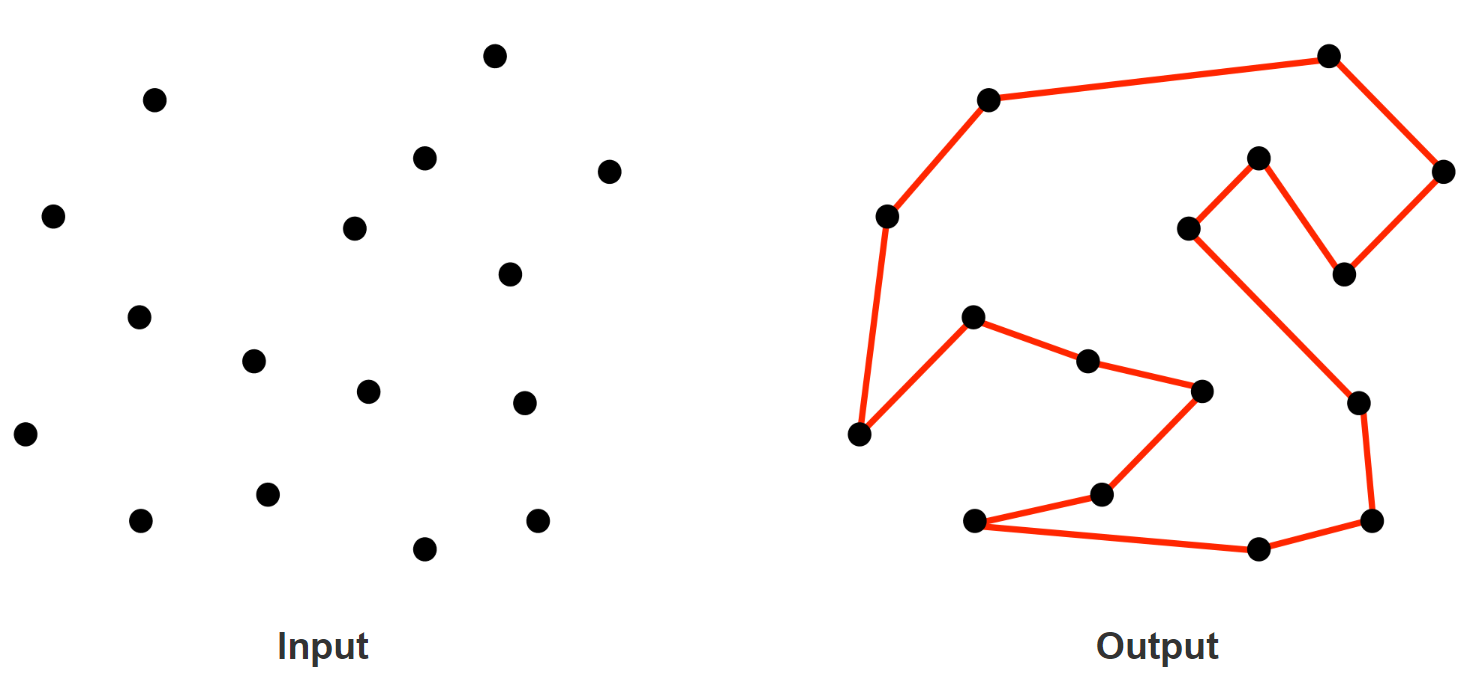
圖片來源：algorist.com

數學模型

符號定義

• $n$: 城市的數量。
• $c_{ij}$: 從城市 $i$ 到城市 $j$ 的距離或成本。
• $x_{ij}$: 決策變量。如果旅行商從城市 $i$ 直接前往城市 $j$，則為 1，否則為 0。

問題輸入

• 城市數量：$n$
• 距離矩陣：$c_{ij}$，表示從城市 $i$ 到城市 $j$ 的距離或成本（對所有 $i,j=1,2,...,n$ 且 $i\ne j$）。

約束條件

每個城市只訪問一次：
$$\sum _{j=1,j\ne i}^n{x}_{ij}=1?i=1,2,\dots ,n$$
$$\sum _{i=1,i\ne j}^n{x}_{ij}=1?j=1,2,\dots ,n$$

$$
\sum_{j=1, j \neq i}^{n} x_{ij} = 1 \quad \forall i = 1, 2, \ldots, n
$$
$$
\sum_{i=1, i \neq j}^{n} x_{ij} = 1 \quad \forall j = 1, 2, \ldots, n
$$

目標函數

最小化總旅行距離或成本：
$$\min \sum _{i=1}^n\sum _{j=1,j\ne i}^n{c}_{ij}{x}_{ij}$$

$$
\min \sum_{i=1}^{n}\sum_{j=1, j \neq i}^{n} c_{ij} x_{ij}
$$

問題輸出

• 訪問城市的順序。

解的空間

旅行商問題的解空間是指所有可能的路徑組合數量。

解空間大小計算

• 對于 $n$ 個城市的 TSP，旅行商從一個城市出發，并有 $(n?1)$ 個城市可以選擇作為第一站。
• 在訪問了第一個城市后，剩下 $(n?2)$ 個城市可以選擇作為下一站，以此類推。
• 最后，旅行商將從最后一個未訪問的城市返回起始城市。

因此，TSP 的解空間大小為所有可能路徑的數量，計算公式為：

$$(n?1)!$$

其中，$(n?1)!$ 表示 $(n?1)$ 的階乘，即 $1\times 2\times 3\times \dots \times (n?2)\times (n?1)$。

解釋

旅行商可以從任何城市開始，但是不同的起點并不會影響各城市在解中的相對順序。每個路徑都可以通過循環移位變換為從特定城市（比如第一個城市）開始的路徑，所以實際上只需考慮從一個固定城市出發的路徑。

車輛路徑問題 (VRP)

問題介紹

車輛路徑問題（英語：Vehicle Routing Problem，VRP）在1959年被首次提出，是TSP的泛化形式，包含TSP問題。問題描述：車隊需要向給定的一組客戶家中取貨或是送貨，需要遍歷的最佳路線集是什么？
值得一提的是，在1959年被提出時，論文名稱是’The truck dispatching problem’，并沒有使用Vehicle Routing Problem的表述。在隨后十多年的相關研究中，也一直沒有直接使用VRP這一名詞的論文。直到Christofides, N.的論文’The vehicle routing problem’于1976年發表后，后續研究普遍采用了VRP的表述。

TSP到VRP的過渡

我們把TSP問題或一個場景表述為一輛空載的卡車從車庫或是車場（出發城市）出發需要到多位客戶的家中（其它城市）取貨物，待取完所有貨物后需要返回車庫。這里有一個潛在的假定，不管所有客戶家中的貨物累加和究竟有多大，這一輛卡車總能全部納入到自己的車廂中并繼續正常行駛。也就是，車輛的運輸能力 $C$ 大于等于所有的貨物量：
$$C\ge \sum _i{q}_i$$
其中 $q_i$ 表述第 $i$ 個客戶家中的貨物量。
但是，當面臨一輛卡車完不成所有的任務量時，也就是：
$$C<\sum _i{q}_i$$
就需要多輛車去完成，或者是一輛車多次往返。
按照論文The truck dispatching problem. Management science 6, 80–91 (1959)里面的介紹，把該條件描述為：
$$C?\sum _i{q}_i$$
并且，文章提出假定一輛車最多只能訪問 $m$ 個點，只有當 $m$ 比較大時，有研究意義，否則的話，求解比較容易，如下：

If $m$ is small, optimal sets of $m$ points may often be determined by inspection of a map which contains the points and the arcs connecting them. One would look for “clusters of points” and determine by trial and error the order in which they should be traversed, taking care that no loop crosses itself. However, when clusters are not present in sufficient numbers or when $m$ is large, this procedure becomes inapplicable. In this case near-best solutions may be obtained by the algorithm in this paper.
如果 $m$ 很小，最優的 $m$ 個點的集合通常可以通過檢查包含這些點和連接它們的弧的地圖來確定。人們會尋找"點的簇集"，并通過試驗和錯誤來確定它們應該按照什么順序遍歷，確保沒有回路交叉。然而，當簇集數量不足或者 $m$ 很大時，這種方法就不適用了。在這種情況下，可以通過本文中的算法獲得近似最優解。

數學模型

符號定義

• $n$: 任務點的數量。
• $P_i$: 第 $i$ 個任務點的位置，($i=1,2,\dots ,n$)。
• $[D]=[d_{ij}]$: 任務點間的距離鄰接矩陣，($i,j=0,1,\dots ,n$)。
• $(Q)=(q_i)$: 各任務點的任務量，($i=1,2,\dots ,n$)。
• $C$: 卡車的容量，滿足 $C>\max (q_i)$。
• $x_{ij}$: 決策變量。如果任務點 $P_i$ 和 $P_j$ 被同一輛車輛訪問，則 $x_{ij}=x_{ji}=1$；如果不被同一輛車輛訪問，則 $x_{ij}=x_{ji}=0$；對于所有 $i$, $x_{ii}=0$。

問題輸入

• 給定 $n$ 個任務點的位置 $P_i$。
• 給定任務點間的距離鄰接矩陣 $[D]$。
• 給定任務點的任務量 $(Q)$。
• 給定卡車的容量 $C。

約束條件

1. 車輛的起點和終點均是車庫 $P_0$。
2. 每個任務點 $P_i$ 除了與車庫 $P_0$ 外，最多與另一個任務點 $P_j$ 被同一個車輛訪問一次。對于所有 $i=1,2,\dots ,n$，有 ${\sum }_{j=0}^n{x}_{ij}=1$。
3. 每輛車輛在任何時候的載荷不得超過其容量 $C$。對于車輛在訪問任務點 $P_i$ 時的載荷量，滿足以下條件：
   $$\sum _{i=1}^n{q}_i{x}_{ij}\le C?j=1,2,\dots ,n$$
   其中，$q_i$ 表示任務點 $P_i$ 的任務量，$x_{ij}$ 表示車輛是否訪問了任務點 $P_i$。

$$\sum_{i=1}^{n} q_i x_{ij} \le C \quad \forall j = 1, 2, \ldots, n$$

優化目標

最小化總行駛距離 $D$：
$$\min D=\sum _{i,j=0}^n{d}_{ij}{x}_{ij}$$

$$\min D = \sum_{i,j=0}^n d_{ij} x_{ij}$$

問題輸出

• 各車輛的行駛路線。

解空間

在車輛路徑問題（VRP）中，我們考慮除起點和終點外的所有車輛行駛路線。這些路線可以排列成一個由 $n$ 個點組成的一維序列 $S$，擁有 $n!$ 種可能性。

特殊情況

假設 $n$ 是 $m$ 的整數倍，且每輛車必須經過 $m$ 個點才能返回車庫。此時，序列 $S$ 只需平均分配給各車輛，解空間仍為 $n!$ 種。

一般情況

如果每輛車經過的點數在 1 到 $m$ 之間，解空間的計算變得復雜。

目前尚沒有發現計算精確解空間大小的文獻， AI 也無法給出確切數字，下面是一個粗略的估算方法。

• 單輛車的最大訪問點數為 $m$，可能的訪問序列數量為排列數 $P(n,m)$。
• 對于 $k$ 輛車，考慮所有可能的序列組合。
• 考慮到車輛間訪問點的重疊，實際解空間小于 $P(n,m{)}^k$。

因此，解空間的上限估算為 $P(n,m{)}^k$。

TSP 與 VRP 對比

對比條目	TSP（旅行商問題）	VRP（車輛路徑問題）
問題描述	給定一個城市列表以及每對城市之間的距離，訪問每個城市一次并返回出發城市的最短路線是什么	車隊需要向給定的一組客戶家中取貨，需要遍歷的最佳路線集是什么？
問題輸入	城市數量，距離矩陣	城市數量，距離矩陣，任務量，卡車容量
約束條件	每個城市僅訪問一次	每個城市僅訪問一次，滿足容量要求
優化目標	最小化總旅行距離	最小化總旅行距離
問題輸出	一個旅行商訪問城市的順序	多個車輛的行駛路線
求解空間	城市序列：$(n?1)!$	城市序列加上車輛任務分配：$n!<S<P(n,m{)}^k$

以n=13，m=5，k=3為例

• TSP解空間：$(n?1)!=(13?1)!=12!=4.79\times 10^8$
• VRP解空間：
  • 下限：$n!=13!=12!=6.23\times 10^9$
  • 上限：$P(n,m{)}^k=P(15,5{)}^3=3.68\times 10^{15}$

---

• 理解本質區別了嗎？
  • 啥是本質，還是迷迷糊糊的😶?🌫?，似乎是還差點，又似乎是還差許多💫。下雪了，開心👻