【C++】：AVL樹

朋友們、伙計們，我們又見面了，本期來給大家解讀一下有關多態的知識點，如果看完之后對你有一定的啟發，那么請留下你的三連，祝大家心想事成！

C 語言專欄：C語言：從入門到精通

數據結構專欄：數據結構

個? 人? 主? 頁?：stackY、

C + + 專欄? ?：C++

Linux 專?欄? ：Linux

1. AVL樹的概念

2. AVL樹節點的定義

3. AVL樹的插入

3.1 AVL樹的旋轉

1. 右單旋

2. 左單旋

3. 先左單旋再右單旋（雙旋）

4. 先右單旋再左單旋（雙旋）

4. AVL樹的驗證?

4.1 AVL樹的性能?

1. AVL樹的概念

二叉搜索樹雖可以縮短查找的效率，但如果數據有序或接近有序二叉搜索樹將退化為單支樹，查找元素相當于在順序表中搜索元素，效率低下。因此，兩位俄羅斯的數學家G.M.Adelson-Velskii和E.M.Landis在1962年發明了一種解決上述問題的方法：

當向二叉搜索樹中插入新結點后，如果能保證每個結點的左右子樹高度之差的絕對值不超過1(需要對樹中的結點進行調整)，即可降低樹的高度，從而減少平均搜索長度。

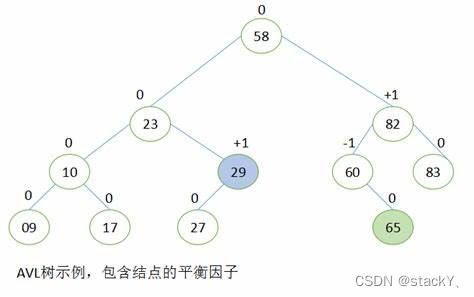
一棵AVL樹或者是空樹，或者是具有以下性質的二叉搜索樹：

它的左右子樹都是AVL樹
左右子樹高度之差(簡稱平衡因子)的絕對值不超過1(-1/0/1)

如果一棵二叉搜索樹是高度平衡的，它就是AVL樹。如果它有n個結點，其高度可保持在
$O(\log N)$ ，搜索時間復雜度 $O(\log N)$ 。

2. AVL樹節點的定義

在這里我們定義AVL樹使用一個pair來存儲數據，關于AVL樹其中除了左右子樹的節點指針，還需要一個記錄父親的節點指針，并且需要存儲一個平衡因子。平衡因子是右子樹的高度減去左子樹的高度。
//AVL樹節點的定義
template<class K, class V>
struct AVLTreeNode
{AVLTreeNode<K, V>* _left;   //左子樹AVLTreeNode<K, V>* _right;  //右子樹AVLTreeNode<K, V>* _parent; //父節點pair<K, V> _kv;             //存儲節點數據的kv模型int _bf;                    //平衡因子//AVLTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr),_parent(nullptr),_kv(kv),_bf(0){}
};

3. AVL樹的插入

AVL樹就是在二叉搜索樹的基礎上引入了平衡因子，因此AVL樹也可以看成是二叉搜索樹。那么AVL樹的插入過程可以分為兩步：

1. 按照二叉搜索樹的方式插入新節點
2. 調整節點的平衡因子

如果插入的節點在左邊，那么就需要將平衡因子--，如果插入的節點在右邊，平衡因子就需要++，并且需要注意的是當平衡因子改變之后，如果為0，代表平衡，不需要其他操作，如果改變之后為1或者-1，那么同樣的也需要對它祖先的平衡因子進行改變，直到它的父節點為空即可停止，如果改變之后的平衡因子為-2或者2，那么就表示出現的不平衡現象，需要進行旋轉。
//插入
bool Insert(const pair<K,V>& kv){//1. 先按照二叉搜索樹的規則將節點插入到AVL樹中Node* cur = _root;Node* parent = nullptr;if (_root == nullptr){_root = new Node(kv);retrun true;}while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->rigth;}elseretrun false;}cur = new Node(kv);if (parent->_kv.first > kv.first){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}//2. 調整節點的平衡因子while (parent){if (parent->_left == cur)    //插入的節點在左邊時，平衡因子--parent->_bf--;else (parent->_right == cur) //插入的節點在右邊時，平衡因子++parent->_bf++;if (parent->_bf == 0)        //判斷平衡因子時候合理break;else if (parent->_bf == 1 || parent->_bf == -1)  //插入新的節點導致高度變化，//所以得依次向上去調整它們父親的平衡因子{cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//平衡出現差錯，需要進行旋轉調整//...}else   //如果平衡因子不為上述情況，那么就不能再繼續了assert(false);}return true;}

3.1 AVL樹的旋轉

如果在一棵原本是平衡的AVL樹中插入一個新節點，可能造成不平衡，此時必須調整樹的結構，使之平衡化。根據節點插入位置的不同，AVL樹的旋轉分為四種：

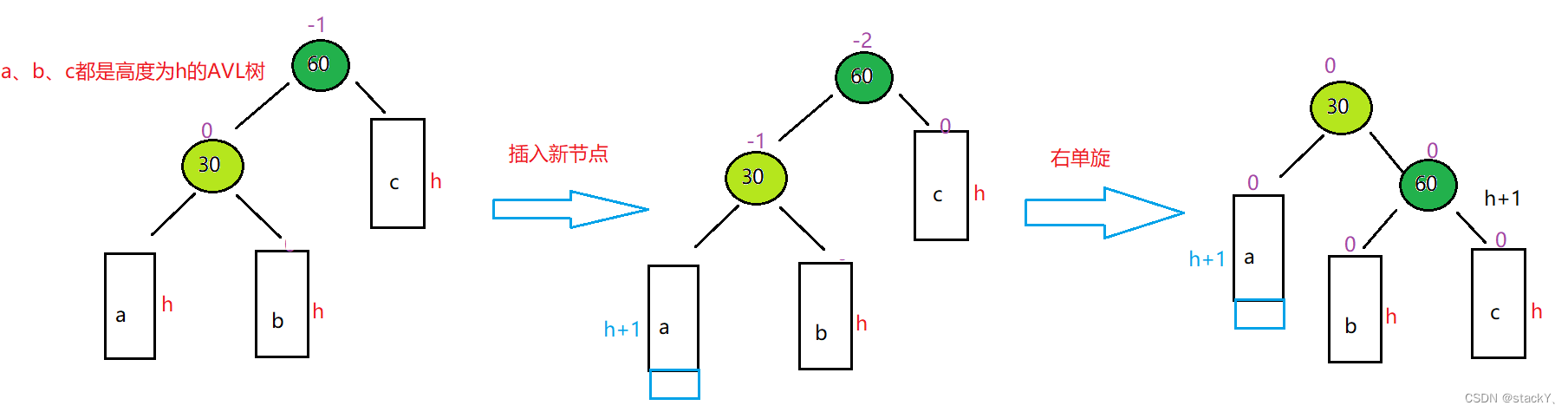
1. 右單旋

新節點插入較高左子樹的左側---左左：右單旋

需要注意的一個點，我們不確定這棵樹是不是另外一棵樹的一個子樹，所以還需要將parent的父親記錄下來，如果這棵樹就是獨立的，那么只需要將subL設置為新的根節點即可，如果是另外一棵樹的子樹，那么就需要將旋轉完之后的樹鏈接在它的祖先上。

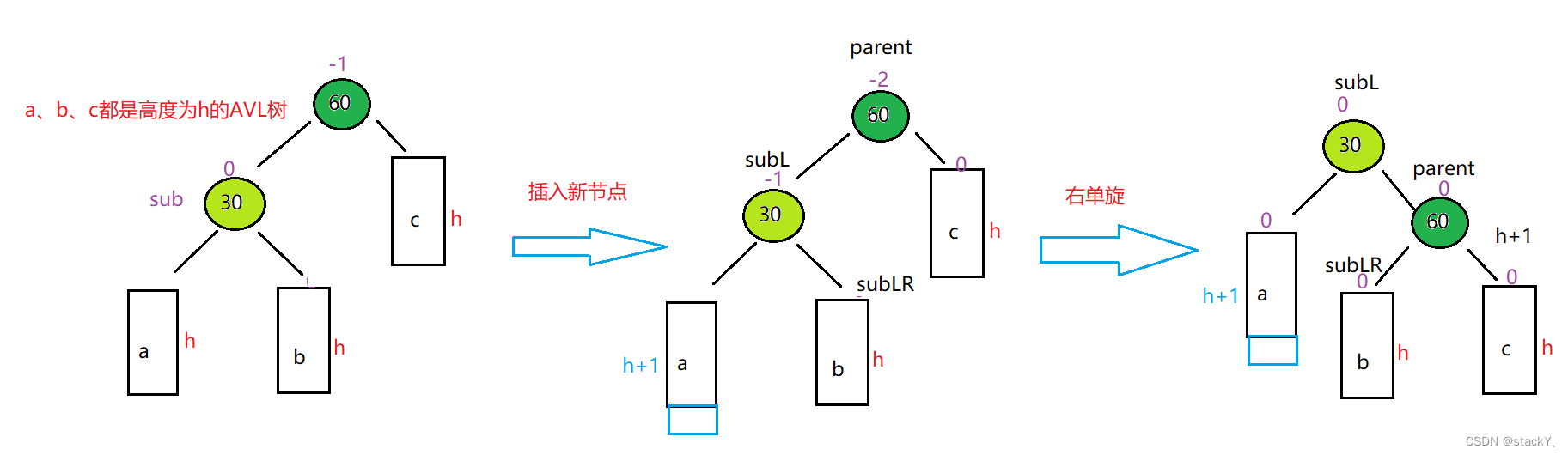
首先將根節點記為parent，因為需要右旋，所以肯定是左邊高往右邊旋轉，所以將parent的左子樹記為subL，將subL的右子樹記為subLR，接下來就需要需要旋轉了，將parent的左指向subLR，然后將subL的右指向parent，這樣子就完成了右旋。

需要注意的是在修改完各各節點的鏈接時，它們原來的父親關系就需要重新設置，比如上面的圖，將parent的父親指向subL，將subLR的父親指向parent（subLR不一定為空，所以需要判斷一下再進行鏈接）此時只需要將各各節點的平衡因子修改即可，在右旋之后可以發現subL和parent的平衡因子都變成了0，所以直接對它們各自的平衡因子修改即可
//右單旋void Rotate_right(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;Node* ppNode = parent->_parent;//旋轉鏈接parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;parent->_parent = subL;//鏈接祖先if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}//修改平衡因子subL->_bf = parent->_bf = 0;}
2. 左單旋

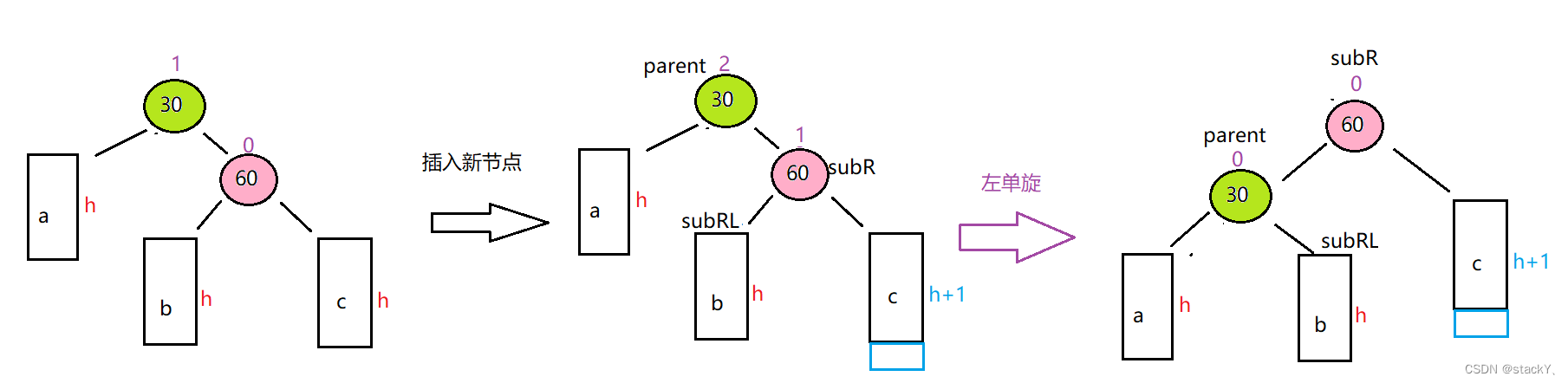
左單旋和右單旋的情況類似，只不過左單旋是右邊高往左邊旋轉，類似的可以參考右單旋的思路。
//左單旋void Rotate_left(Node* parent){Node* subR = parent->_right;  //右子樹的節點Node* subRL = subR->_left;    //Node* ppNode = parent->_parent;//旋轉->重新鏈接subR->_left = parent;parent->_parent = subR;parent->_right = subRL;if (subRL)subRL->_parent = parent;//鏈接祖先if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (ppNode->_left == parent)ppNode->_left = subR;elseppNode->_right = subR;subR->_parent = ppNode;}//修改平衡因子parent->_bf = subR->_bf = 0;}
3. 先左單旋再右單旋（雙旋）

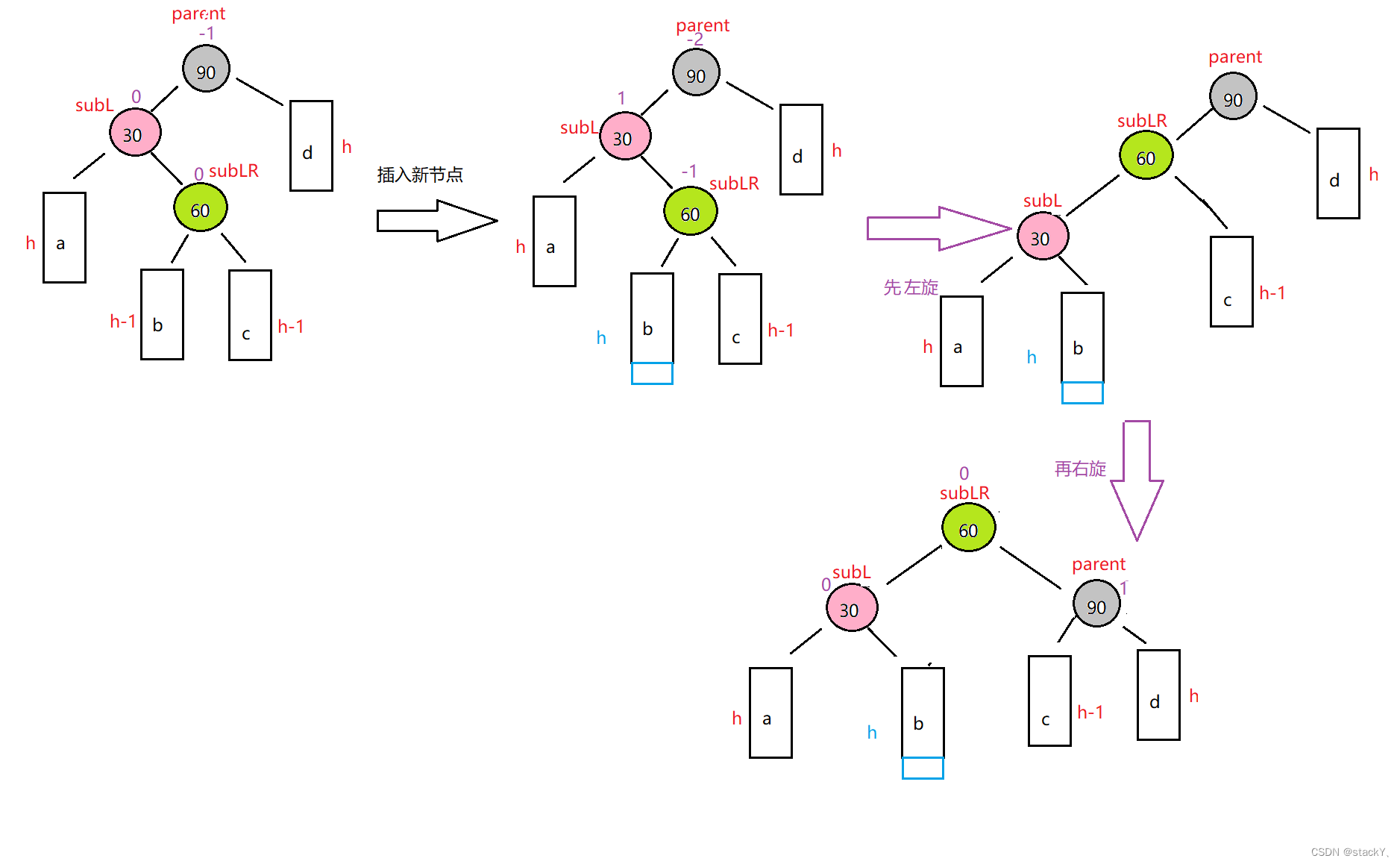
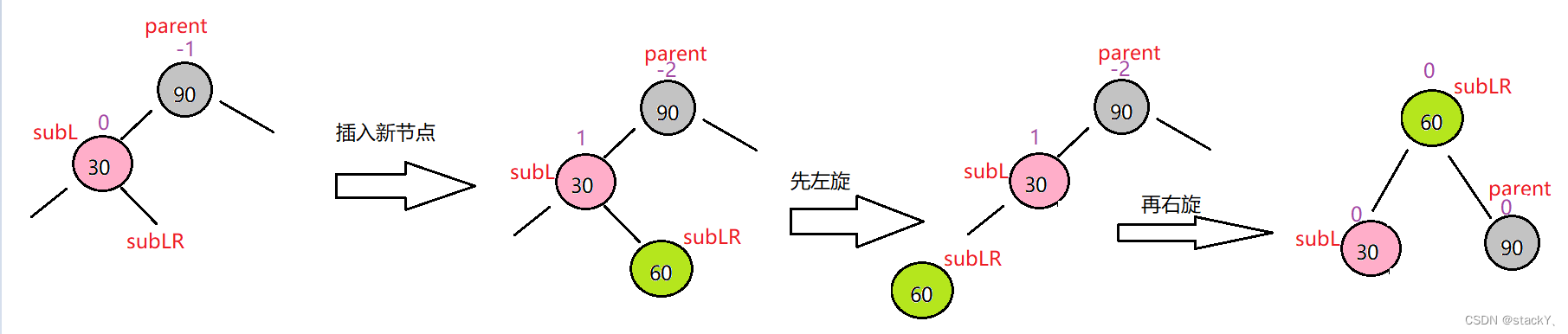
左右雙旋在這里依舊存在三種情況：

①插入在subLR的左邊

②插入在subLR的右邊

③subLR就是新插入的節點

雙旋的情況可以看到是一個折線的樣子，根據偏轉的方向來確定首先向哪邊旋轉，先將根節

點記為parent，再將parent的左記為subL，將subL的右記為subLR，先以subL為根進行左單旋，然后再以parent為根進行右單旋。然后根據上述三種情況修改平衡因子。

可以根據subLR的平衡因子來修改parent、subL、subLR的平衡因子：

①如果subLR的平衡因子是-1，那么在雙旋完之后，需要將parent的平衡因子修改為1，將其他兩個修改為0。

②如果subLR的平衡因子是1，那么在雙旋完之后，需要將subL的平衡因子修改為-1，將其他兩個修改為0。

③如果subLR的平衡因子是0，那么parent、subL、subLR的平衡因子修改為0。
//左右雙旋void Rotate_left_right(Node* parent){Node* subL = parent->-left;Node* subLR = subL->_right;//記錄插入之后的平衡因子int bf = subLR->_bf;//先左旋Rotate_left(subL);//再右旋Rotate_right(parent);//修改平衡因子if (bf == 0)   //本身就是新插入的節點{subL->_bf = subLR->_bf = parent->_bf = 0;}else if (bf == -1)  //左邊插入{parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}else if (bf == 1)  //右邊插入{subL->_bf = -1;parent->_bf = 0;subLR->_bf = 0;}else{assert(flase);}}
4. 先右單旋再左單旋（雙旋）

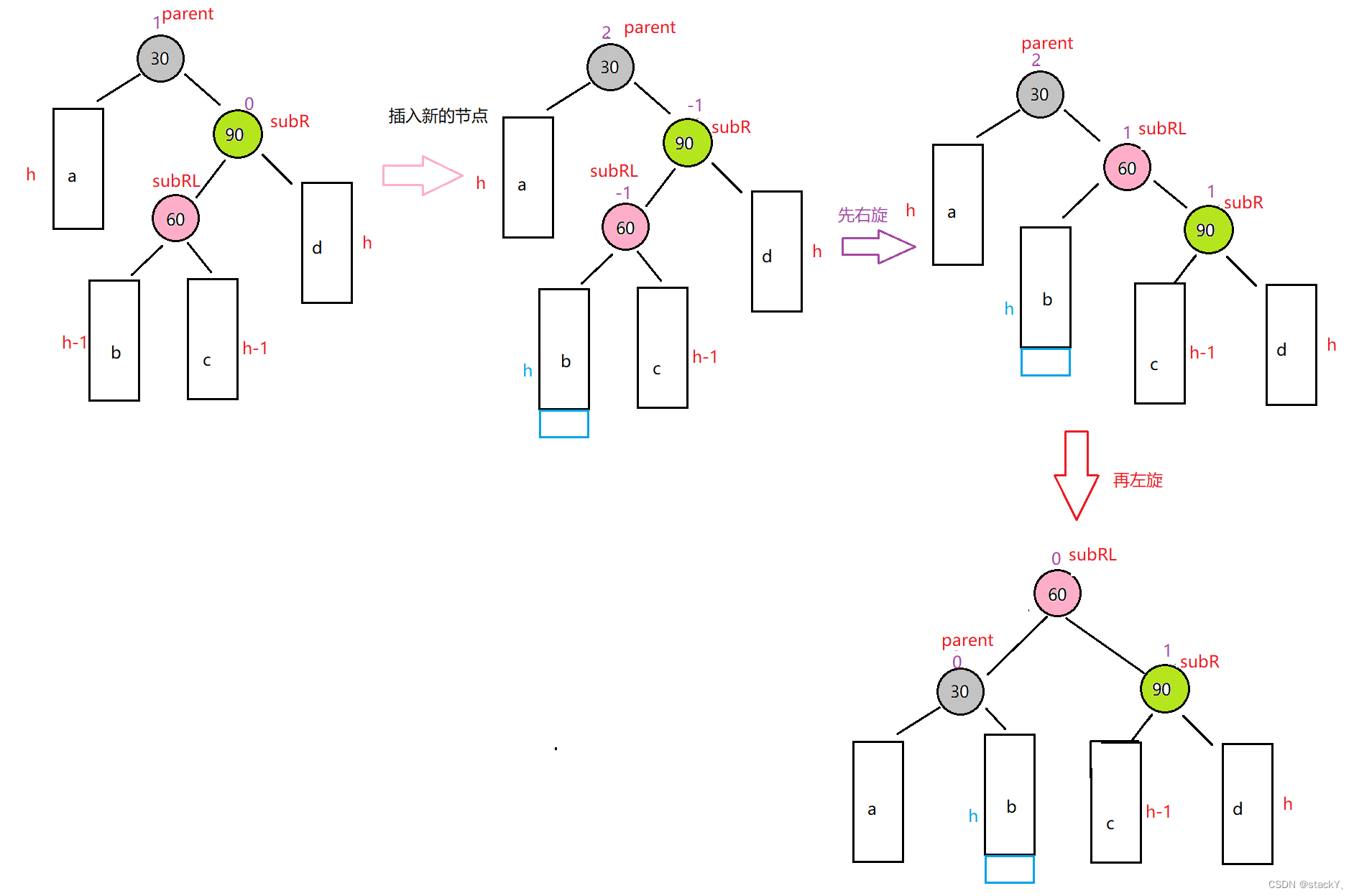
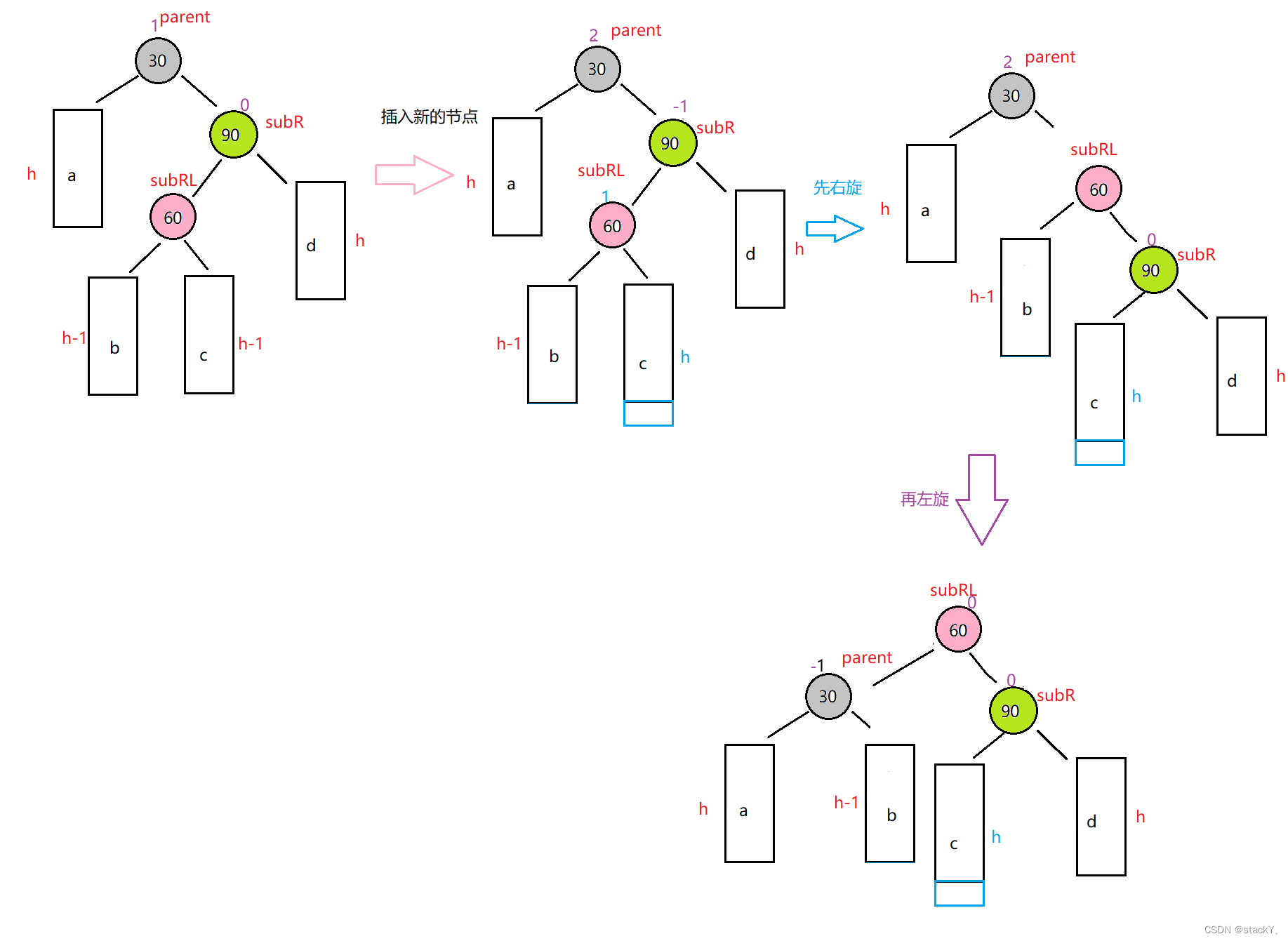
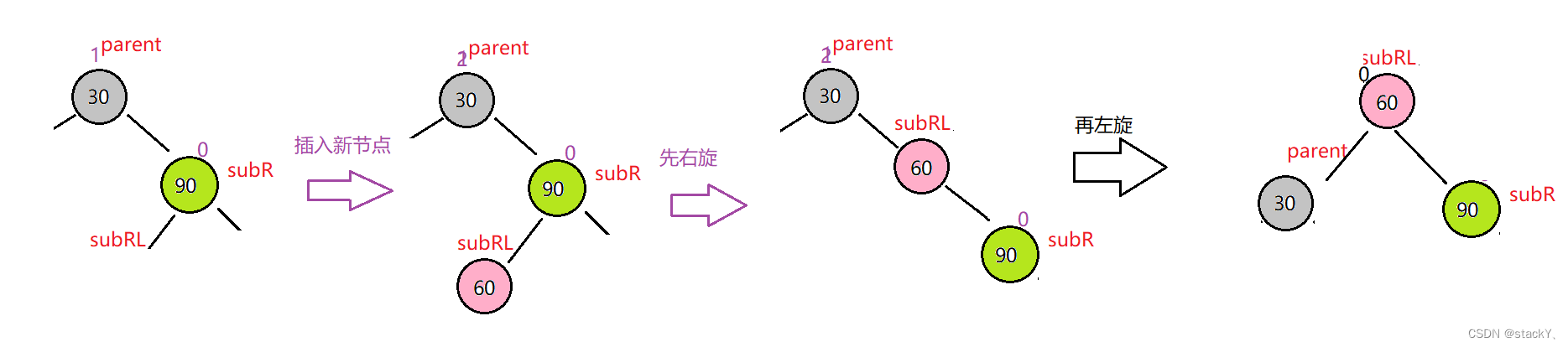
同樣的這里也存在三種情況：

①插入在subRL的左邊

②插入在subRL的右邊

③subRL就是新插入的節點

右左雙旋的邏輯和左右雙旋的邏輯一樣，可以參考上面的。
//右左雙旋void Rotate_right_left(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;Rotate_right(subR);Rotate_left(parent);if (bf == 0){subR->_bf = subRL->_bf = parent->_bf = 0;}else if (bf == -1){subR->_bf = 1;parent->_bf = 0;subRL->_bf = 0;}else if (bf == 1){parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}elseassert(false);}

解決完插入中的旋轉問題之后我們將旋轉融入到插入的整個代碼中：

bool Insert(const pair<K,V>& kv){//1. 先按照二叉搜索樹的規則將節點插入到AVL樹中Node* cur = _root;Node* parent = nullptr;if (_root == nullptr){_root = new Node(kv);retrun true;}while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->rigth;}elseretrun false;}cur = new Node(kv);if (parent->_kv.first > kv.first){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}//2. 調整節點的平衡因子while (parent){if (parent->_left == cur)    //插入的節點在左邊時，平衡因子--parent->_bf--;else (parent->_right == cur) //插入的節點在右邊時，平衡因子++parent->_bf++;if (parent->_bf == 0)        //判斷平衡因子時候合理break;else if (parent->_bf == 1 || parent->_bf == -1)  //插入新的節點導致高度變化，//所以得依次向上去調整它們父親的平衡因子{cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//平衡出現差錯，需要進行旋轉調整if (parent->_bf == 2 && cur->_bf == 1)         //左單旋情況Rotate_left(parent);else if (parent->_bf == -2 && cur->_bf == -1)  //右單旋情況Rotate_right(parent);else if (parent->_bf == -2 && cur->_bf == 1)   //左右雙旋情況Rotate_left_right(parent);else if (parent->_bf == 2 && cur->_bf == -1)   //右左雙旋情況Rotate_right_left(parent);// 1、旋轉讓這顆子樹平衡了// 2、旋轉降低了這顆子樹的高度，恢復到跟插入前一樣的高度，所以對上一層沒有影響，不用繼續更新break;}else   //如果平衡因子不為上述情況，那么就不能再繼續了assert(false);}return true;}

4. AVL樹的驗證?

AVL樹是在二叉搜索樹的基礎上加入了平衡性的限制，因此要驗證AVL樹，可以分兩步：

1. 驗證其為二叉搜索樹

如果中序遍歷可得到一個有序的序列，就說明為二叉搜索樹

2. 驗證其為平衡樹

每個節點子樹高度差的絕對值不超過1(注意節點中如果沒有平衡因子)
節點的平衡因子是否計算正確
?
//判斷是否平衡bool IsBalance(){return _IsBalance(_root);}//計算樹的高度int _Height(Node* root){if (root == nullptr)return 0;int leftHeight = _Height(root->_left);   //左子樹的高度int rightHeight = _Height(root->_right); //右子樹的高度//返回左右子樹高度較高的那一顆樹+1return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}bool _IsBalance(Node* root){if (root == nullptr)return true;int leftHeight = _Height(root->_left);   //左子樹的高度int rightHeight = _Height(root->_right); //右子樹的高度if (rightHeight - leftHeight != root->_bf){cout << root->_kv.first << "平衡因子異常" << endl;return false;}//右子樹-左子樹高度不超過2則為AVL樹return abs(rightHeight - leftHeight) < 2&& _IsBalance(root->_left)&& _IsBalance(root->_right);}

4.1 AVL樹的性能?

AVL樹是一棵絕對平衡的二叉搜索樹，其要求每個節點的左右子樹高度差的絕對值都不超過1，這樣可以保證查詢時高效的時間復雜度，即 $O(\log N)$ 。但是如果要對AVL樹做一些結構修改的操作，性能非常低下，比如：插入時要維護其絕對平衡，旋轉的次數比較多，更差的是在刪除時，有可能一直要讓旋轉持續到根的位置。因此：如果需要一種查詢高效且有序的數據結構，而且數據的個數為靜態的(即不會改變)，可以考慮AVL樹，但一個結構經常修改，就不太適合。