🔥博客主頁：?【小扳_-CSDN博客】
?感謝大家點贊👍收藏?評論????

文章目錄

????????1.0 從前序與中序遍歷序列來構造二叉樹

? ? ? ? 1.1 實現從前序與中序遍歷序列來構造二叉樹思路? ?

? ? ? ? 1.2 代碼實現從前序與中序遍歷序列來構造二叉樹

? ? ? ? 2.0 從中序與后序遍歷序列構造二叉樹

? ? ? ? 2.1 實現從中序與后序遍歷序列后遭二叉樹思路

? ? ? ? 2.2 代碼實現從中序與后序遍歷序列來構造二叉樹

? ? ? ? 3.0 根據后綴表達式創建二叉樹

? ? ? ? 3.1 實現后綴表達式創建二叉樹思路

? ? ? ? 3.2 代碼實現后綴表達式創建二叉樹

? ? ? ? ?4.0 相同的樹

? ? ? ? 4.1 實現判斷兩顆樹是否相同思路

? ? ? ? 4.2 代碼實現相同樹

? ? ? ? ?5.0 另一顆樹的子樹

????????5.1 實現判斷是否為另一顆樹的子樹

????????5.2 代碼實現判斷是否為另一顆樹的子樹

---

????????1.0 從前序與中序遍歷序列來構造二叉樹

題目：

????????給定兩個整數數組?preorder?和?inorder?，其中?preorder?是二叉樹的先序遍歷，?inorder?是同一棵樹的中序遍歷，請構造二叉樹并返回其根節點。

示例 1:

輸入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
輸出: [3,9,20,null,null,15,7]

OJ鏈接：

105.?從前序與中序遍歷序列構造二叉樹

? ? ? ? 1.1 實現從前序與中序遍歷序列來構造二叉樹思路? ?

????????具體思路為：前序遍歷的流程先是訪問根節點，到左子樹，再到右子樹的順序；中序遍歷的流程先是左子樹，到訪問根節點，再到右子樹。因此，在前序的序列中的第一個元素就是該樹的根節點的值，然后再通過中序的序列中遍歷找根節點。接著就可以將其中序的序列進行拆分，在中序序列中根節點的值的左邊部分的序列為左子樹，在中序序列中根節點的值的右邊部分序列為右子樹。又接著將前序序列進行拆分，從索引為 1 開始，長度為：與中序序列中左子樹的序列數量是一致的，將這一部分稱為左子樹；從索引 （1+長度）開始到該序列的結束，將這一部分稱為右子樹。接下來就是子問題了，通過遞歸，找到當前節點的左右子樹。

? ? ? ?具體例子：前序序列 pre = {3,9,20,15,7}，中序序列 in = {9,3,15,20,7} 。先找到該樹的節點值 int rootValue = pre[0]， TreeNode root = new TreeNode(rootValue)，創建該樹的根節點。接著對中序序列遍歷來找到根節點的值，i == 1 ，在中序序列中找左右子樹：在索引在該區間 [0,1）是節點的左子樹，而在索引為?[2,5）區間是節點的右子樹。在前序序列中找左右子樹：在索引為 [1,2）是該節點的左子樹，而在索引為 [2,5）區間是節點的右子樹。

? ? ? ? 子問題：那么現在得到了左子樹的前序序列 pre = { 9 } ，左子樹的中序序列 in = { 9 }，接下來的流程跟以上的流程是一樣的，先找到該子樹的根節點值 9 ，然后創建一個值為 9 的根節點。接著，遍歷中序序列來找到根節點的值，該根節點的左部分就是左子樹，該節點的右部分就是右子樹。那么這里的左右子樹都為空，因此節點為 9 的根節點沒有左右子樹了。

? ? ? ? 往上回溯：來到根節點值為 3 的節點。現在得到了右子樹的前序序列 pre = {20,15,7} ，右子樹的中序序列 in = {15,20,7} ，接下來的過程是一摸一樣的，先找到該子樹的根節點值為 20 ，創建值為 20 的根節點。然后在中序序列中進行遍歷找到根節點的左右子樹 ：左子樹序列為 {15}，右子樹序列為 {7}，接著在前序序列中找左右子樹：左子樹序列為 {15}，右子樹序列為 {7} 。又得到了左右前中序列，按同樣的道理繼續下去即可，通過上面的結論，當左子樹前序 {15} 與左子樹中序 {15} 一樣時，那么在當前的節點值為 15 的根節點沒有左右子樹了。同理，當右子樹前序 {7} 與右子樹中序 {7} 一樣時，那么在當前的節點值為 7 的根節點沒有左右子樹了。

? ? ? ? 最后回溯，根節點值為 20 的左子樹的根節點為 15，右子樹的根節點為 7 ，鏈接起來，一直回溯到結束返回的最后的節點就是該樹的根節點（值為 1 的根節點）。

? ? ? ? 需要注意的是：注意左閉右開。因為是同一顆樹，在前序中的左右子樹的長度跟中序中的左右子樹的長度是一樣的。

? ? ? ? 1.2 代碼實現從前序與中序遍歷序列來構造二叉樹

    //根據前序與中序來構造二叉樹public TreeNode prevAndInOrderConstructTree(int[] prevOrder, int[] inOrder) {if (prevOrder.length == 0) {return null;}int rootValue = prevOrder[0];TreeNode root = new TreeNode(rootValue);for (int i = 0; i < inOrder.length; i++) {if (inOrder[i] == rootValue) {int[] inLeft = Arrays.copyOfRange(inOrder,0,i);int[] inRight = Arrays.copyOfRange(inOrder,i+1,inOrder.length);int[] prevLeft = Arrays.copyOfRange(prevOrder,1,i + 1);int[] prevRight = Arrays.copyOfRange(prevOrder,i+1,inOrder.length);root.left = prevAndInOrderConstructTree(prevLeft,inLeft);root.right = prevAndInOrderConstructTree(prevRight,inRight);}}return root;}

? ? ? ? 只要某一個序列無論是前序或者是中序序列的長度為 0 ，都代表創建二叉樹過程結束了。

? ? ? ? 2.0 從中序與后序遍歷序列構造二叉樹

題目：

????????給定兩個整數數組?inorder?和?postorder?，其中?inorder?是二叉樹的中序遍歷，?postorder?是同一棵樹的后序遍歷，請你構造并返回這顆?二叉樹?。

示例 1:

輸入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
輸出：[3,9,20,null,null,15,7]

OJ鏈接：

106.?從中序與后序遍歷序列構造二叉樹

? ? ? ? 2.1 實現從中序與后序遍歷序列后遭二叉樹思路

? ? ? ? 具體思路為：中序的序列先訪問左子樹，再訪問根節點，最后到右子樹。后序的序列先訪問左子樹，再訪問右子樹，最后才到根節點。因此，可以從后序序列中的最后一個元素得到根節點的值，然后利用該值來創建根節點。接著，在中序序列中遍歷查找根節點的值，在中序序列中根節點值左邊的序列為左子樹序列，在中序序列中根節點的右邊為右子樹的序列。再接著再后序中獲取左子樹的序列：從索引為 0 開始長度是中序序列得到的左子樹的長度；從后序序列中獲取右子樹序列：除了左子樹的序列和根節點值元素，其余就是右子樹的序列了。接下來就是子問題了，遞歸下去，返回當前的根節點。

? ? ? ? 具體例子：中序序列 in = {9,3,15,20,7}，后序序列 post = {9,15,7,20,3}，通過后序得到該樹的根節點的值 3，由這個值來創建值為 3 的根節點。接著通過遍歷中序序列，找到值為 3 來定位左右子樹，左子樹的序列為：{9} ，右子樹的序列為：{15,20,7} 。再從中序序列中定位左右子樹，左子樹為：{9}，右子樹為：{15，7，20} 。現在得到了左右中后序列，中序左子樹：{9} ，后序左子樹：{9}，通過后序得到根節點，再從中序定位該子樹的根節點，這里根節點值為 9 的根節點的左右子樹均為 null 。接著回溯，返回的該子樹的根節點。

? ? ? ? 再到右子樹中序 {15,20,7} ，右子樹后序 {15,7,20}，通過后序序列的最后一個值來創建該子樹的根節點，在中序中遍歷找到該根節點的值，定位該節點的左右子樹。中序的左子樹序列 {15}，右子樹序列 {7}；后序的左子樹序列 {15}，后序的右子樹序列 {7} 。

? ? ? ? 再接著遞歸，得到左子樹中序 {15} ，左子樹后序 {15}。通過后序的最后一個元素就是根節點的值來創建該子樹的根節點，然后在中序中定位該根節點的左右子樹，這里的左右子樹都為 null ，返回根節點即可。得到右子樹中序 {7}，右子樹后序 {7}，通過后序的最后一個元素為根節點的值來創建該子樹的根節點，然后在中序中定位該根節點的左右子樹，恰好，這里的左右子樹都為 null ，返回根節點即可。

? ? ? ? 最后回溯過程，根節點值為 1 的節點的左子樹的根節點為 9 的節點，右子樹的根節點為 20 的節點。

? ? ? ? 2.2 代碼實現從中序與后序遍歷序列來構造二叉樹

    //根據中序與后序來構造二叉樹public TreeNode inAndPostConstructTree(int[] inOrder, int[] postOrder) {if (inOrder.length == 0) {return null;}int rootValue = postOrder[postOrder.length-1];TreeNode root = new TreeNode(rootValue);for (int j = 0; j < inOrder.length; j++) {if (rootValue == inOrder[j]) {int[] inLeft = Arrays.copyOfRange(inOrder,0,j);int[] inRight = Arrays.copyOfRange(inOrder,j+1,inOrder.length);int[] postLeft = Arrays.copyOfRange(postOrder,0,j);int[] postRight = Arrays.copyOfRange(postOrder,j,postOrder.length-1);root.left = inAndPostConstructTree(inLeft,postLeft);root.right = inAndPostConstructTree(inRight,postRight);}}return root;}

? ? ? ? 需要注意的定位左右子樹的序列長度，中序與后序的左右子樹都是一一對應的。也因此，當無論任意一個序列結束，都代表著構造二叉樹過程結束。

? ? ? ? 3.0 根據后綴表達式創建二叉樹

????????后綴表達式也叫逆波蘭表達式，是一種不需要括號的表達式表示方法。在后綴表達式中，運算符總是在操作數的后面，因此可以通過從左到右掃描表達式來創建二叉樹。

? ? ? ? 3.1 實現后綴表達式創建二叉樹思路

? ? ? ? 具體思路為：若遇到數字將其壓入棧中；若遇到操作符時，將棧中的右左元素彈出棧，操作符節點進行鏈接彈出來的左右子樹，需要注意的是，第一個彈出來的是右操作數，第二個才是左操作數。鏈接完之后，將其壓入棧中即可。循環結束條件為：將后綴表達式遍歷完就結束。最后返回棧中的棧頂元素，就是該樹的根節點。

? ? ? ? 3.2 代碼實現后綴表達式創建二叉樹

    //根據后綴表達式創建二叉樹public TreeNode suffixCreateTree(String[] s) {LinkedList<TreeNode> stack = new LinkedList<>();for (int i = 0; i < s.length; i++) {String ch = s[i];switch (ch) {case "+","-","*","/" -> {TreeNode right = stack.pop();TreeNode left = stack.pop();TreeNode t = new TreeNode(ch);t.right = right;t.left = left;stack.push(t);}default -> {stack.push(new TreeNode(ch));}}}return stack.peek();}

? ? ? ? ?4.0 相同的樹

題目：

????????給你兩棵二叉樹的根節點?p?和?q?，編寫一個函數來檢驗這兩棵樹是否相同。

如果兩個樹在結構上相同，并且節點具有相同的值，則認為它們是相同的。

示例 1：

輸入：p = [1,2,3], q = [1,2,3]
輸出：true

OJ鏈接：

100.?相同的樹

? ? ? ? 4.1 實現判斷兩顆樹是否相同思路

? ? ? ? 具體思路為：使用遞歸實現，第一種情況：若一個子樹為 null ，另一個子樹不為 null ，返回 false ；第二種情況：若兩個子樹都為 null ，則返回 true 。第三種情況：若兩個子樹的根節點的值不相同時，返回 false 。子過程，判斷完左子樹，還需判斷右子樹。

? ? ? ? 4.2 代碼實現相同樹

class Solution {public boolean isSameTree(TreeNode p, TreeNode q) {if( p != null && q == null || p ==null && q != null) {return false;}if(p == null && q == null ){return true;}if(p.val != q.val) {return false;}return isSameTree(p.left, q.left) && isSameTree(p.right,q.right);}
}

? ? ? ? 5.0 另一顆樹的子樹

題目：

????????給你兩棵二叉樹?root?和?subRoot?。檢驗?root?中是否包含和?subRoot?具有相同結構和節點值的子樹。如果存在，返回?true?；否則，返回?false?。

二叉樹?tree?的一棵子樹包括?tree?的某個節點和這個節點的所有后代節點。tree?也可以看做它自身的一棵子樹。

示例 1：

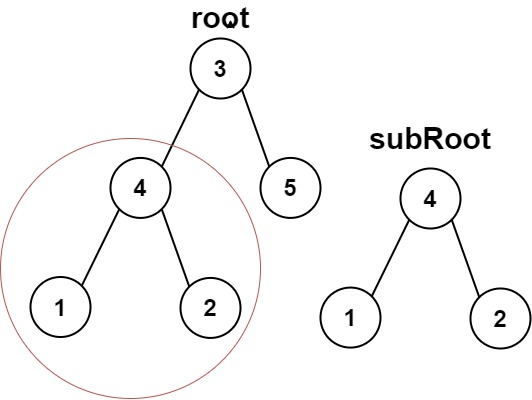
輸入：root = [3,4,5,1,2], subRoot = [4,1,2]
輸出：true

OJ鏈接:

572.?另一棵樹的子樹

? ? ? ? ?5.1 實現判斷是否為另一顆樹的子樹

? ? ? ? 具體思路為：最根本的問題就是判斷是否為相同的樹，判斷該樹的子樹與另一顆子樹是否相同，不斷遞歸下去，只要相同就返回 true 。直到最后遞歸結束都沒有匹配，則返回 false 。

? ? ? ? 5.2 代碼實現判斷是否為另一顆樹的子樹

class Solution {public boolean isSubtree(TreeNode root, TreeNode subRoot) {if(root == null) {return false;}if(isSameTree(root,subRoot)) {return true;}if(isSubtree(root.left,subRoot)) {return true;}if(isSubtree(root.right,subRoot)) {return true;}return false;}public boolean isSameTree(TreeNode p, TreeNode q) {if( p != null && q == null || p ==null && q != null) {return false;}if(p == null && q == null ){return true;}if(p.val != q.val) {return false;}return isSameTree(p.left, q.left) && isSameTree(p.right,q.right);}
}