個人主頁：元清加油_【C++】,【C語言】,【數據結構與算法】-CSDN博客

個人專欄：http://t.csdnimg.cn/ZxuNL

?????????????????http://t.csdnimg.cn/c9twt

前言：這個專欄主要講述遞歸遞歸、搜索與回溯算法，所以下面題目主要也是這些算法做的 ?

我講述題目會把講解部分分為3個部分：
1、題目解析

2、算法原理思路講解

3、代碼實現

一、求根節點到葉節點數字之和

題目鏈接：?求根節點到葉節點數字之和

題目：

給你一個二叉樹的根節點?root?，樹中每個節點都存放有一個?0?到?9?之間的數字。

每條從根節點到葉節點的路徑都代表一個數字：

• 例如，從根節點到葉節點的路徑?1 -> 2 -> 3?表示數字?123?。

計算從根節點到葉節點生成的?所有數字之和?。

葉節點?是指沒有子節點的節點。

示例 1：

輸入：root = [1,2,3]
輸出：25
解釋：
從根到葉子節點路徑 1->2 代表數字 12
從根到葉子節點路徑 1->3 代表數字 13
因此，數字總和 = 12 + 13 = 25

示例 2：

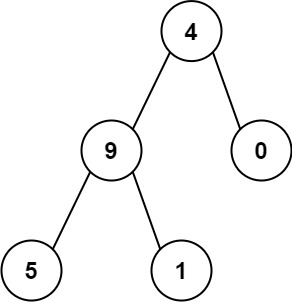
輸入：root = [4,9,0,5,1]
輸出：1026
解釋：
從根到葉子節點路徑 4->9->5 代表數字 495
從根到葉子節點路徑 4->9->1 代表數字 491
從根到葉子節點路徑 4->0 代表數字 40
因此，數字總和 = 495 + 491 + 40 = 1026

提示：

• 樹中節點的數目在范圍?[1, 1000]?內
• 0 <= Node.val <= 9
• 樹的深度不超過?10

二、解法??

題目解析

這道題目的意思是：給我們一棵二叉樹，讓我們計算從根節點到葉節點生成的?所有數字之和?。

例如：

示例 ：

從根到葉子節點路徑 4->9->5????????????????代表數字 495
從根到葉子節點路徑 4->9->1????????????????代表數字 491
從根到葉子節點路徑 4->0???????????????????代表數字 40
因此，數字總和 = 495 + 491 + 40 = 1026

??算法原理思路講解?

注意：我們在做遞歸這一類題目是要將遞歸看作一個黑盒，我們不管他是如何實現的，我們就相信他一定可以幫助我們完成目標

遞歸思路：
1、設計函數頭（尋找重復子問題，并且將遞歸函數看作一個黑盒）。

2、設計函數體（只關心一個子問題，并解決它）

3、設計函數出口（遞歸的終止條件）

算法思路：

根據題目意思可得，我們可以使用一個前序遍歷

在前序遍歷的過程中，我們可以往左右?樹傳遞信息，并且在回溯時得到左右?樹的返回值。遞歸函數可以幫我們完成兩件事：

把上面翻譯一下就是?

例如對于節點9來說

1、節點9將?節點的數字（4）與自己的數字9結合在一起成49傳遞到下一層

2、當遇到節點5的時候，就不再向下傳遞信息，?是將整合的結果（495）返回

??1、設計函數頭

int dfs(TreeNode* root, int num)

（1）?返回值：當前?樹計算的結果（數字和）?

（2）參數 num：遞歸過程中往下傳遞的信息（?節點的數字）

2、設計函數體（只關心一個子問題，并解決它）

• 當遇到空節點的時候，說明這條路從根節點開始沒有分?，返回 0；
• 結合?節點傳下的信息以及當前節點的 val，計算出當前節點數字 presum；
• 如果當前結點不是葉?節點，將 presum 傳到左右?樹中去，得到左右?樹中節點路徑的數字和，然后相加后返回結果。

presum = presum * 10 + root->val;int ret = 0;
if(root->left) ret += dfs(root->left, presum);
if(root->right) ret += dfs(root->right, presum);
return ret;

3、設計函數出口

?如果當前結點是葉?節點，直接返回整合后的結果 presum

if(root->left == nullptr && root->right == nullptr)return presum;

以上思路就講解完了，大家可以先自己先做一下

• 時間復雜度：O(n)，其中 n 是二叉樹的節點個數。對每個節點訪問一次。
• 空間復雜度：O(n)，其中 n 是二叉樹的節點個數。空間復雜度主要取決于遞歸調用的棧空間，遞歸棧的深度等于二叉樹的高度，最壞情況下，二叉樹的高度等于節點個數，空間復雜度為 O(n)。

代碼實現

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int dfs(TreeNode* root, int presum){presum = presum * 10 + root->val;if(root->left == nullptr && root->right == nullptr)return presum;int ret = 0;if(root->left) ret += dfs(root->left, presum);if(root->right) ret += dfs(root->right, presum);return ret;}int sumNumbers(TreeNode* root) {return dfs(root,0);}
};