?圖形學不等于 OpenGL,不等于光線追蹤,而是一套生成整個虛擬世界的方法
記得有個概念叫光柵化,就是把三維虛擬世界的事物顯示在二維的屏幕上,這里就涉及到觀察變換
觀察變換,叫viewing transformation,包括視圖變換和投影變換,投影變換又分為正交投影變換和透視投影變換
目錄
視圖變換
投影變換
正交投影變換
透視投影變換
視圖變換
怎么理解這個視圖變換呢,閆神舉了個例子,比如說要拍張照片,那么把人物和場景擺放好就是模型變換,而找一個好位置放好攝像機并調好角度就是視圖變換,而最后拍照成像的這個過程就是投影變換

怎么實現這個視圖變換呢?我們首先來規定好攝像機的擺放參數,有一個位置,攝像機的朝向(往左往右看),還有一個向上的方向(類似于歪頭)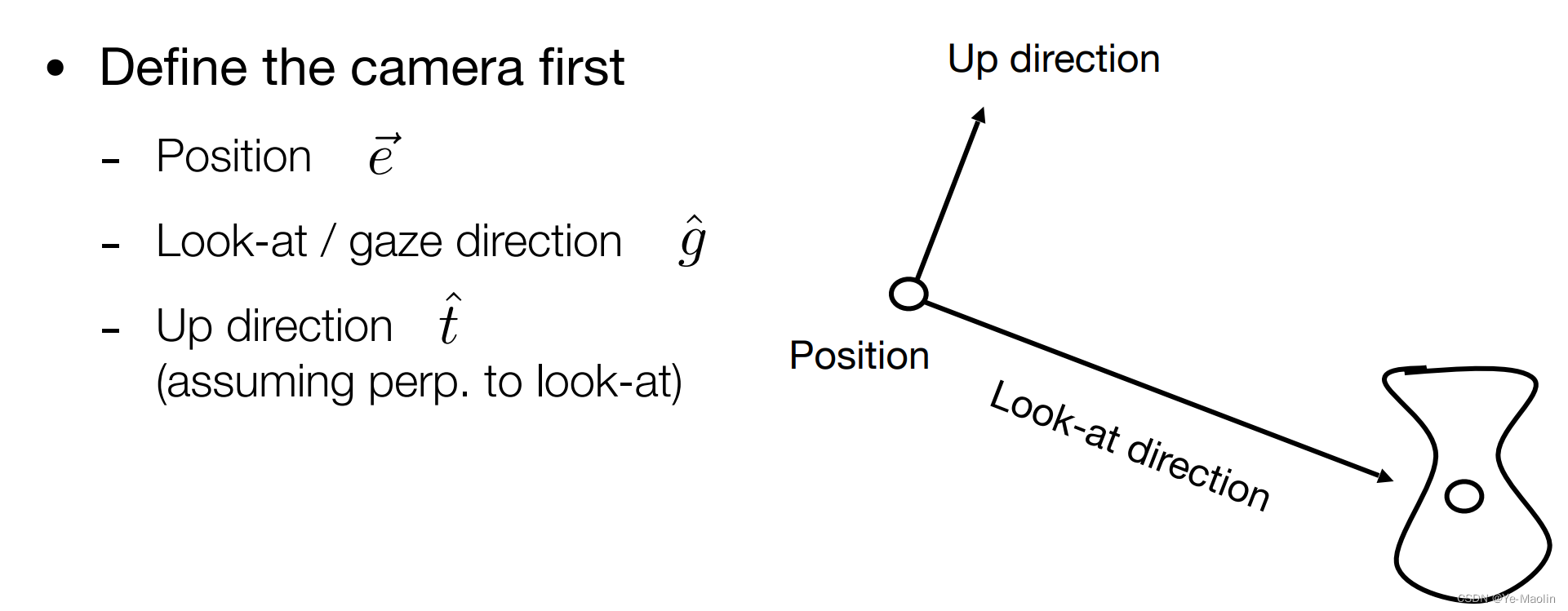
為了方便,于是約定俗成的把這個攝像機的位置放在原點處,然后讓攝像機朝向z軸的負方向,向上的方向為y軸正方向
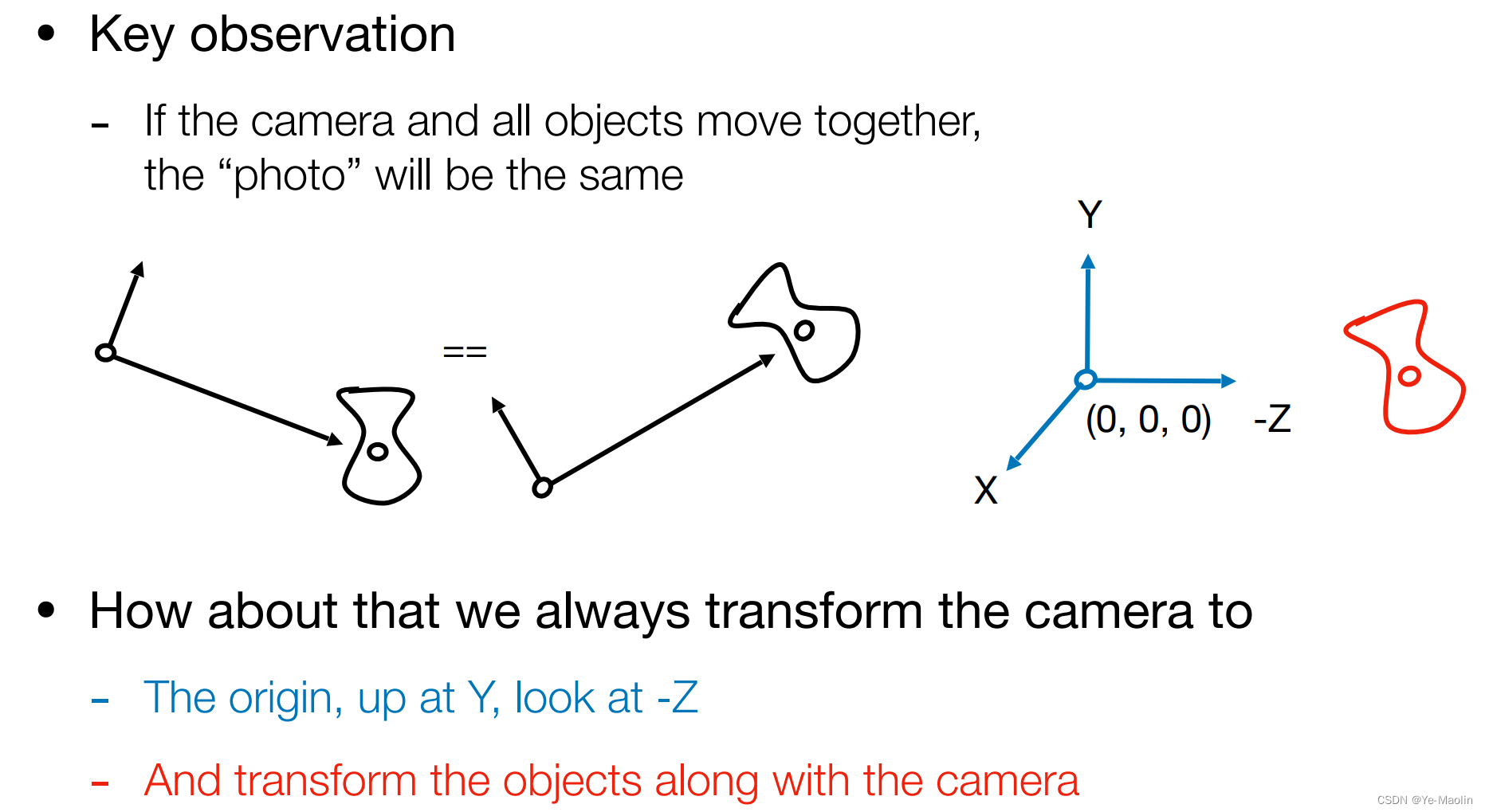
那么如何把一個攝像機移到原點并且旋轉到我們需要的方向呢?
我們可以先平移在旋轉,平移這個簡單,直接就能寫出變換矩陣來
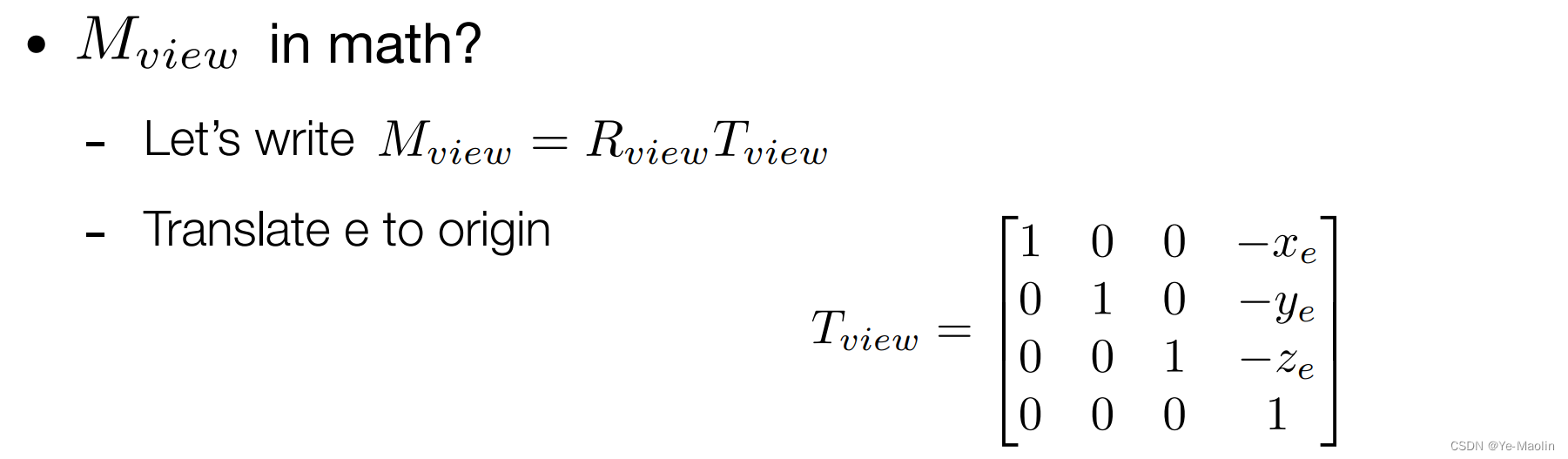
旋轉呢?如果直接考慮從g旋轉到-z,t旋轉到y,以及g×t旋轉到x,這個比較復雜,但是反過來旋轉就比較簡單的可以寫出變換矩陣,所以我們需要的變換矩陣就是這個簡單變換矩陣的逆矩陣,又因為旋轉矩陣是正交矩陣,正交矩陣的逆矩陣就是其本身的轉置矩陣,所以這個簡單的旋轉矩陣轉置就是我們需要的旋轉矩陣

投影變換
投影變換就是為了實現將三維的事物展示在二維上
這個透視投影呢就是近大遠小,而正交投影就是相當于這個攝像機放在無限遠處,那么這樣近處和遠處的大小看起來也是一樣的了

正交投影變換
正交投影變換就是相當于把所有的點都移到XoY這個平面上,相當于這個z坐標不要了
為了顯示所有的點,我們將所有的點都限制在[-1,1]里面來
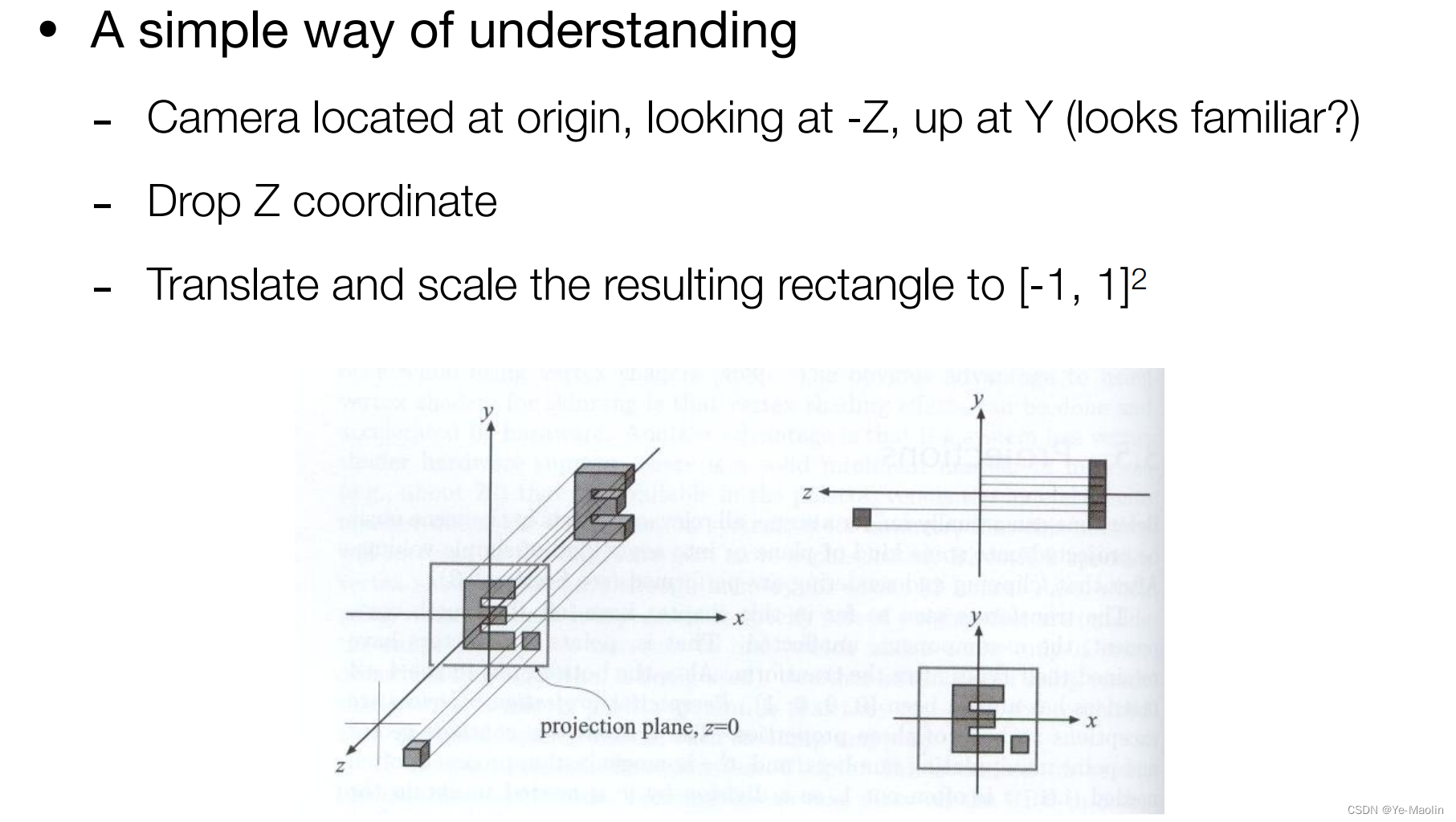
但是這樣分不清遠近,因此我們希望限制在一個正方體里面去,這個叫做標準的正方體,記為
?[l, r] x [b, t] x [f, n]
這個l和r是left和right,就是x方向的左右,b和t呢是bottom和top,對應y方向的上下,而這個f<n是far和near,對應z方向的遠近,那為什么遠比近小呢?這是因為我們的攝像機是看向-z方向的
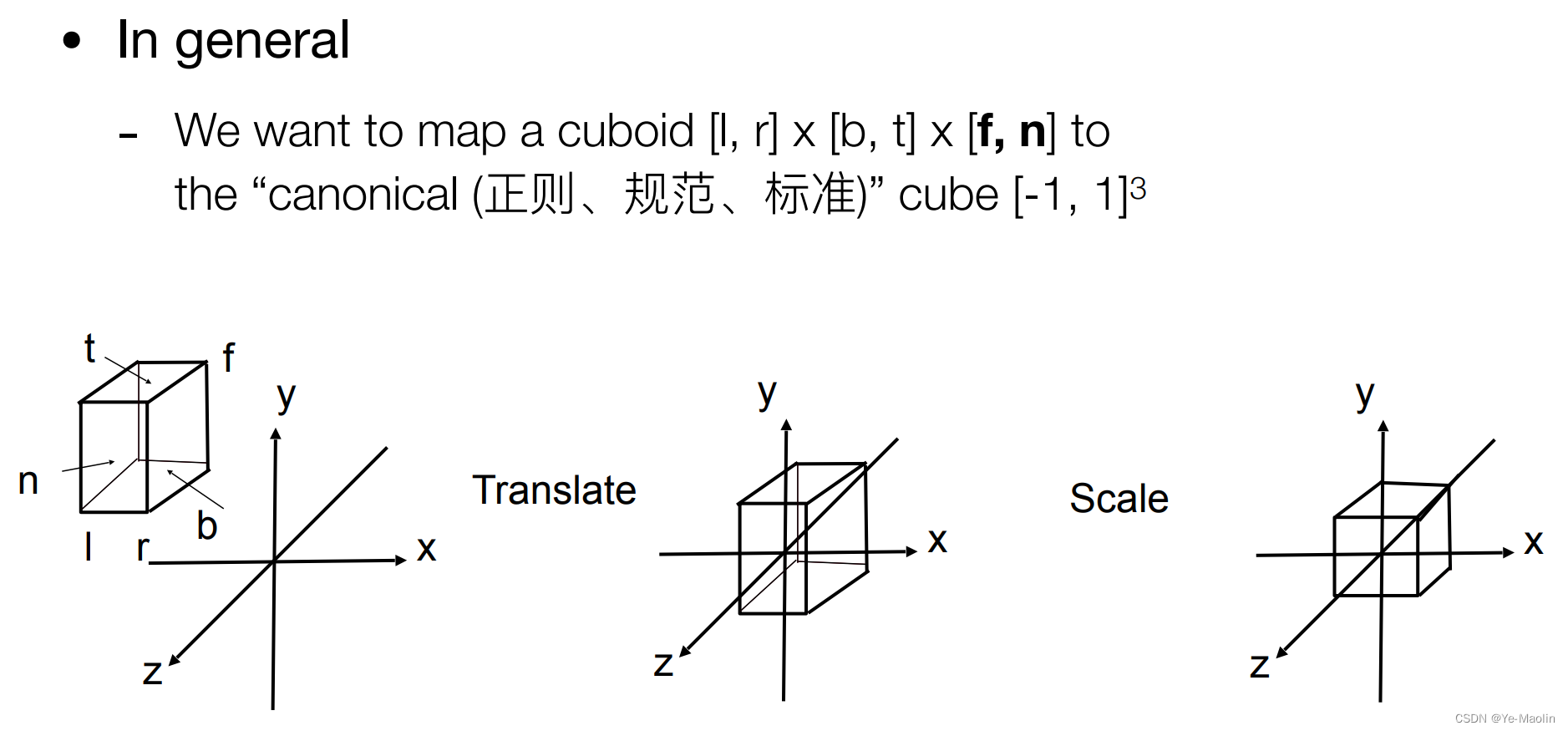
因此對于一個場景,我們通過平移和縮放兩種變換就可以把它限制在這個標準的正方體里面去
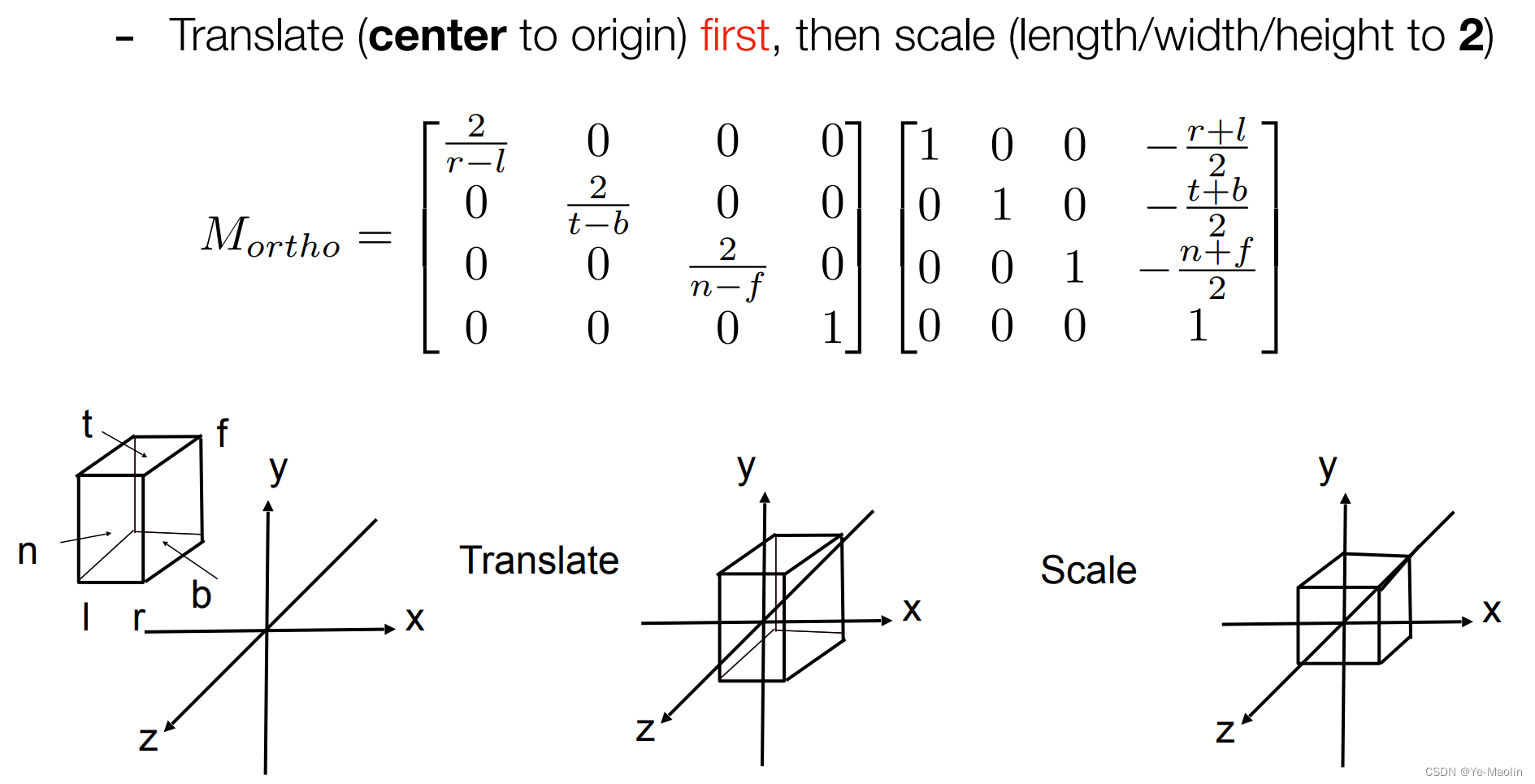
透視投影變換
透視投影比較常見,歐幾里得說過,在一個平面中,永不相交的兩條直線是平行線,但是透視投影卻使得平行線可以看起來是相交的
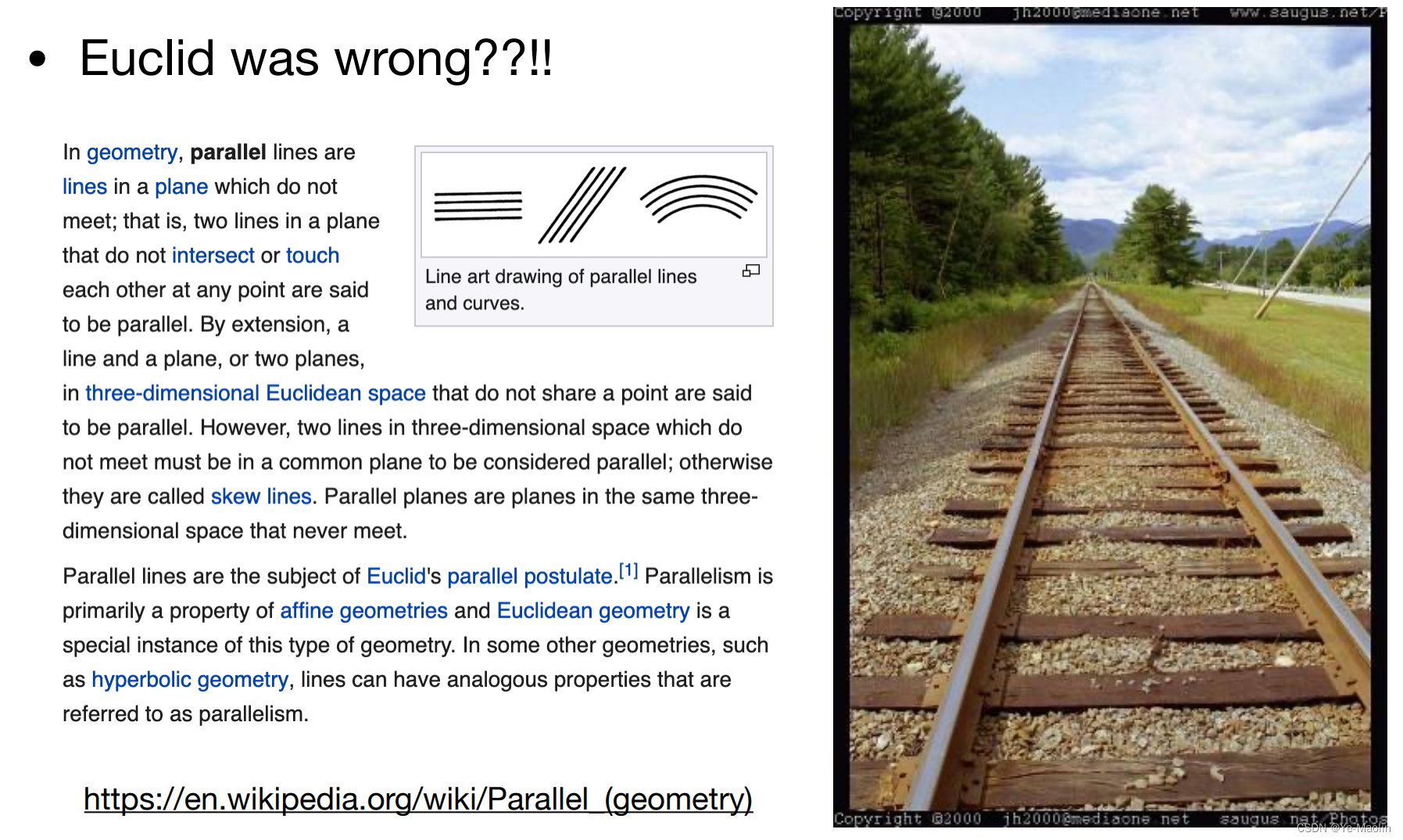
在我們開始之前,我們再回顧一下,在齊次坐標系中,對于一個點而言,如果我們直接對每個維度都乘以某個不為0的系數,那么這個點是不變的,這個點還是這個點對吧

那我們怎么來做這個投影變換呢?
實際上,我們想做的就是把這個截錐體給擠壓成這個長方體,然后再做一次正交投影就行了
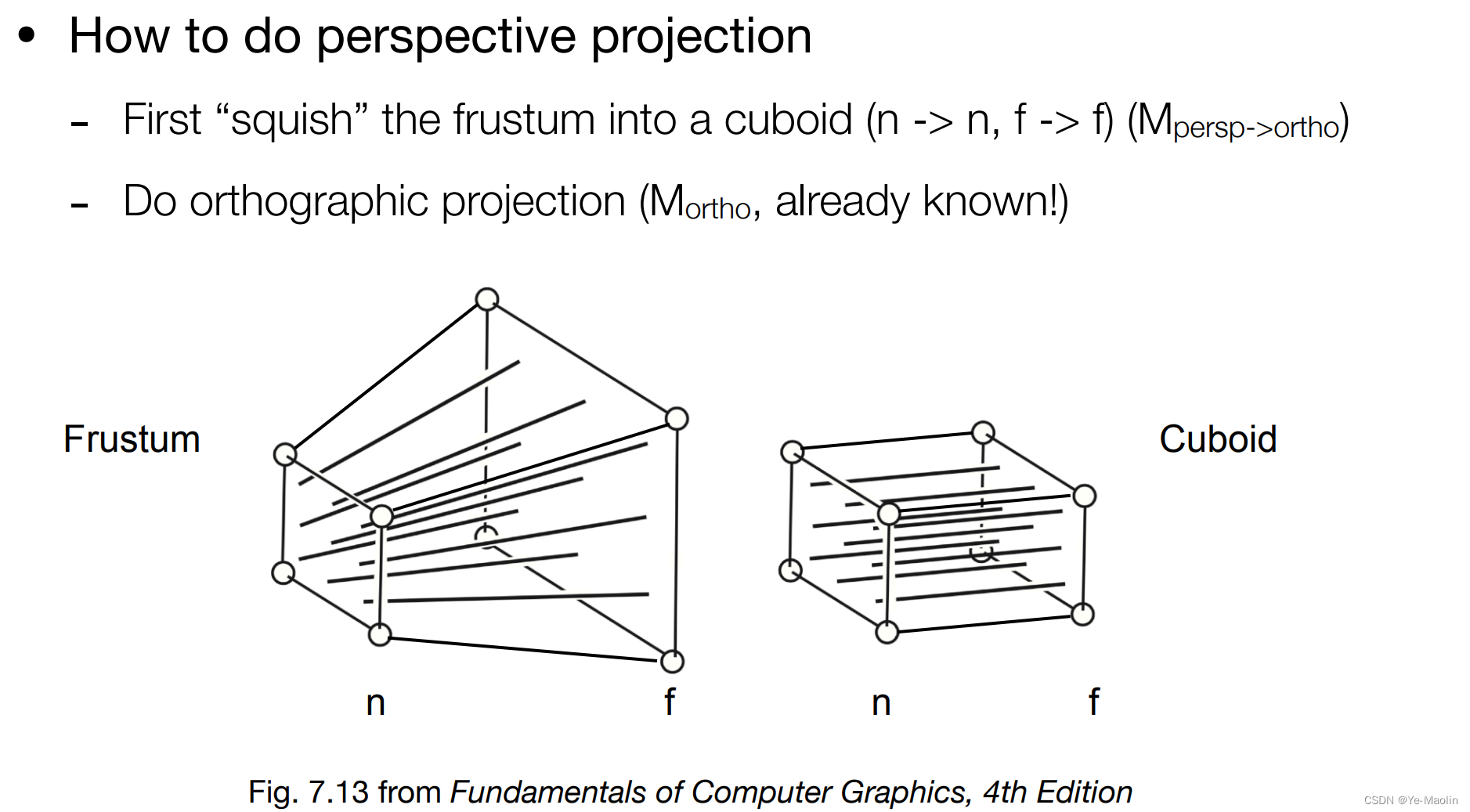
怎么擠壓呢,我們可以取某個點來分析,這里用到相似三角形的原理,相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比
我們先取x和y做分析哈,那么擠壓后的這個x和y就可以通過先前近平面的n和遠平面的z的比值乘以x和y得到
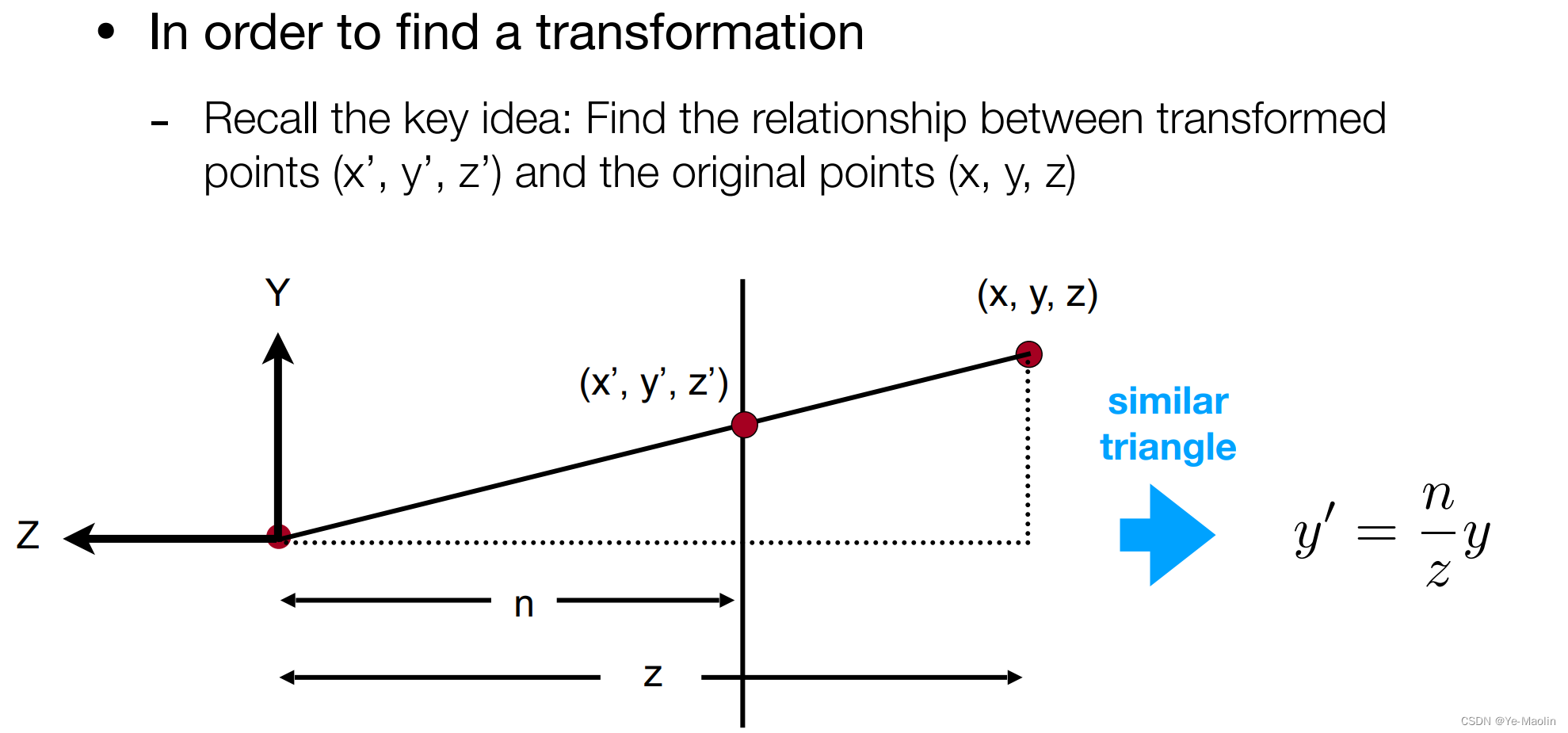 ?
?
因此我們就可以找到一個這么一個對應關系使得這個點擠壓過去,但是這個z會變成什么樣我們還不清楚
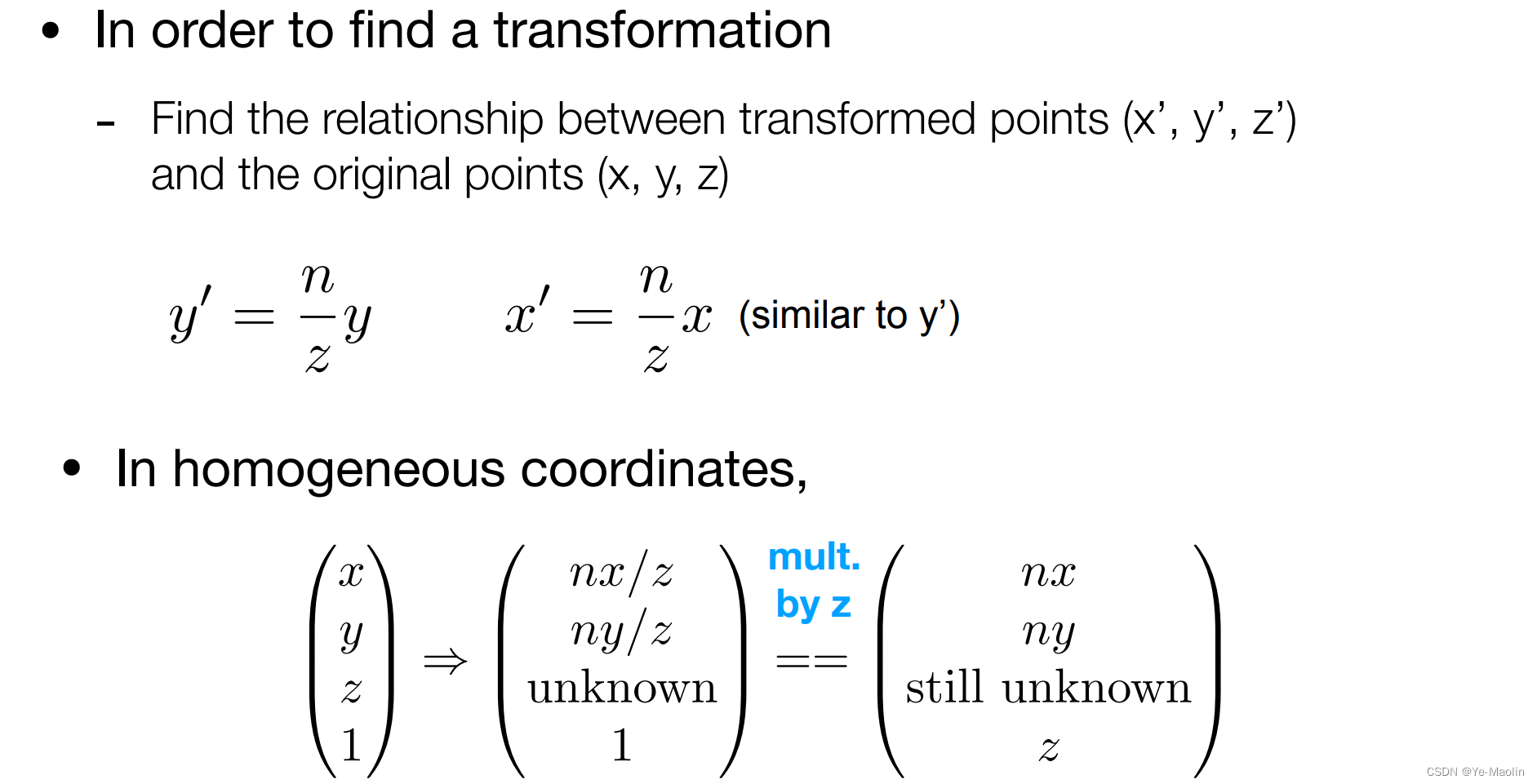
那么現在這個從透視投影變換到正交投影的變換矩陣已經有了雛形了
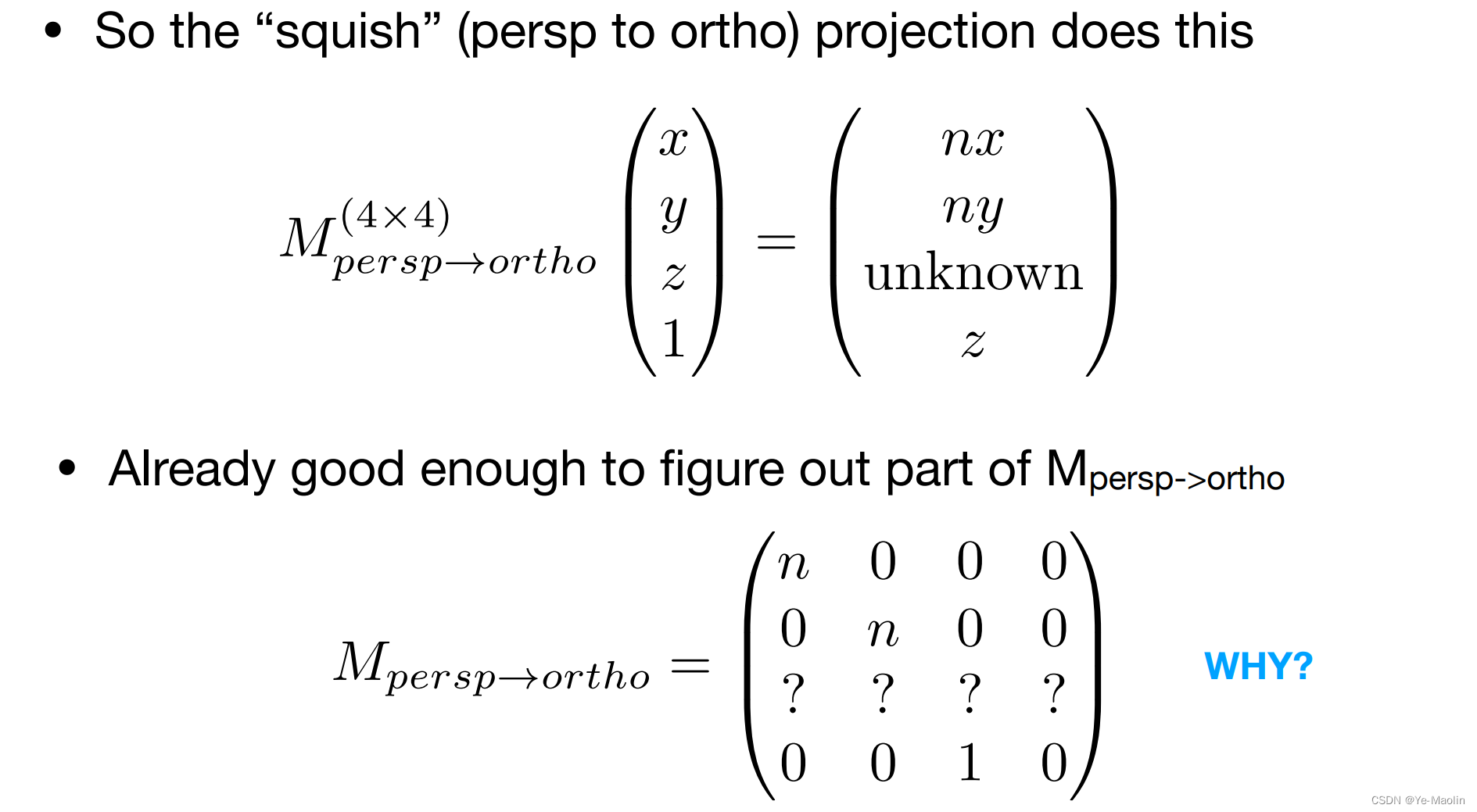 ?
?
怎么解決第三行呢?
我們注意到近平面上的點在擠壓后是不會發生變換的,同時遠平面上的點的z坐標也不會發生變化
因此對于一個點(x,y,n,1)在擠壓后應該還是(x,y,n,1),那么乘以z,也就是乘以n,這個第三行的結果應該是n2,那么這樣的話,第三行應該長成(0,0,A,B)這個樣,只有這樣計算出來的結果才會和x和y沒有關系
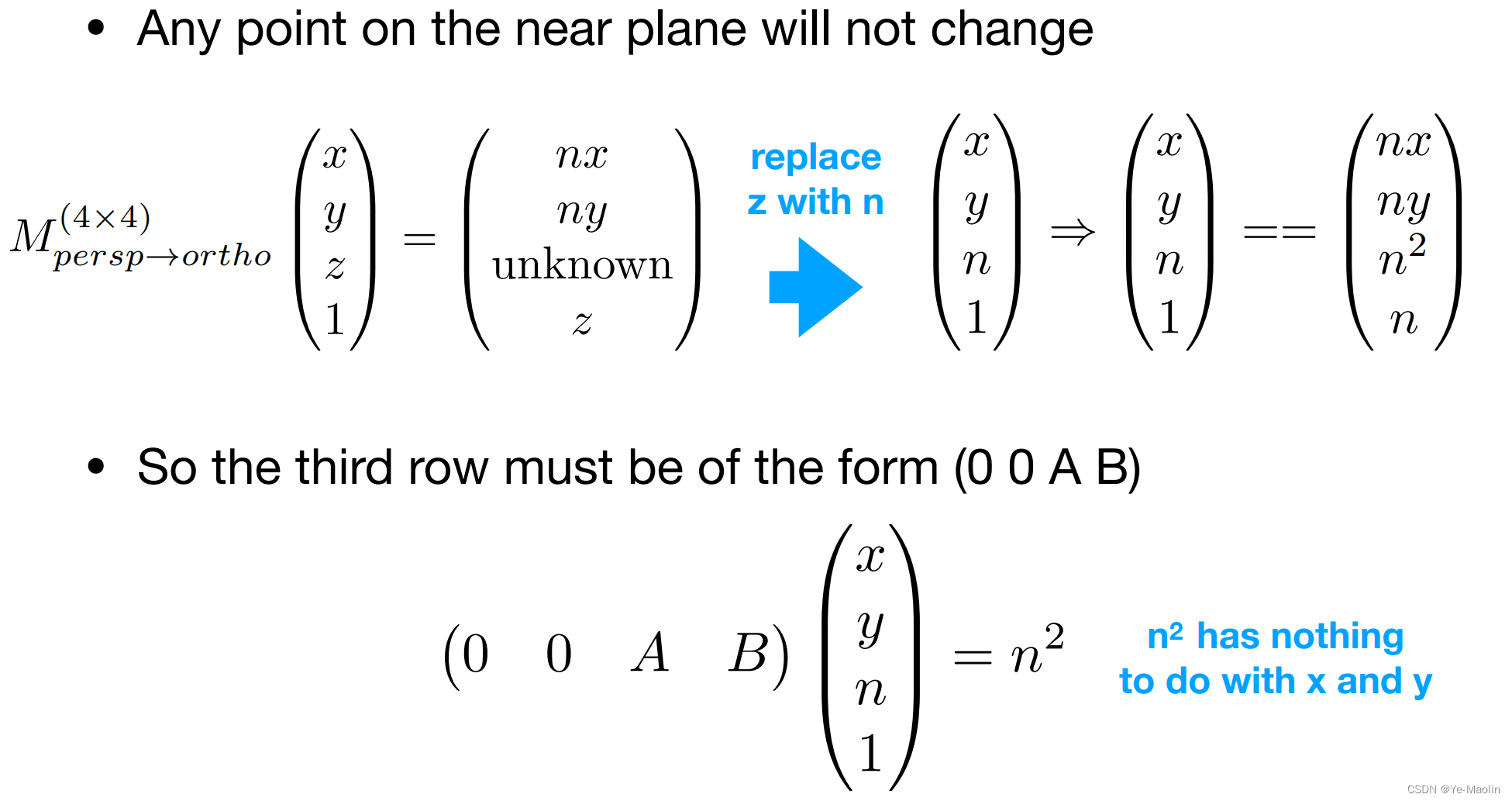
那么再加上遠平面上的點擠壓后z不變的結果,我們可以得到一個二元一次方程組
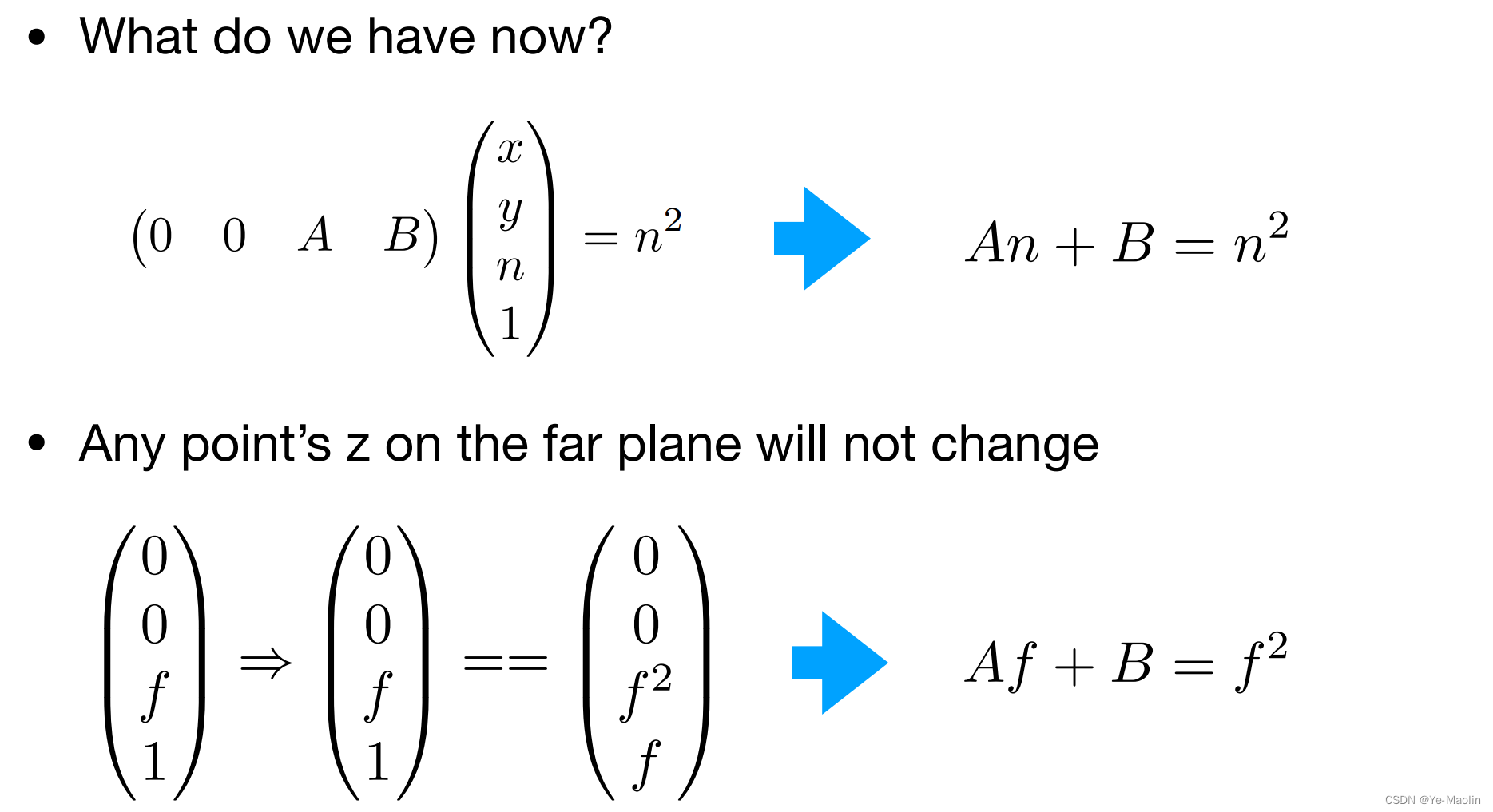
進而可以得到A和B的解,那么這個變化矩陣就找到了

這節課的最后,閆神留了個問題,在擠壓的過程中,這個z坐標會如何變化,是變遠呢還是變近了呢,還是不變呢?





)












)
