整數以及浮點數在內存中的存儲

一.整數在內存當中的存儲

數據在內存中是以十六進制補碼的形式進行存儲的。

原碼表示法簡單易懂，適用于乘法，但用原碼表示的數進行加減運算比較復雜，當兩數相加時，如果同號則數值相加，但是進行減法時要先比較絕對值的大小，然后大數減去小數，最后還要給結果選擇恰當的符號。

而負數用補碼表示，加法運算只需要一個加法器就可以實現了，不用再配減法器，可以將符號位和數值域統一處理，此外補碼與原碼相互轉換，其運算過程是相同的，不需要額外的硬件電路。

而1個十六進制可以表示4個二進制位，在內存中查看變量時，只用看（32/4）8位二進制代碼即可

#include<stdio.h>
int main()
{int hh = 15;return 0;
}

再來看一下負數在內存中的情況

#include<stdio.h>
int main()
{int hh = -15;return 0;
}

此時顯示的變量hh在內存中的情況為ff ff ff f1

原碼hh=-15為10000000 00000000 00000000 00001111? 負數最高符號位為1

? ? ? ? ? ?反碼為11111111? ? 11111111? ? ?11111111? ? 11110000

? ? ? ? ? ?補碼為11111111? ? ?11111111? ? ?11111111? ? 11110001

按照一個十六進制位等于4個二進制，將補碼可轉變為 ff? ff ff f1

大小端字序存儲

什么是大小端字序存儲

大小端字序存儲其實就是字節在內存中存儲時的存儲順序。

如果數據的低位字節內容保存在內存的高地址處，而高字節內容保存在內存的低地址處，那么就是大端存儲模式

如果數據的高位字節內容保存在內存的高地址處，而低字節內容保存在低地址處，那么就是小端存儲模式

比如15，它的十六進制補碼為00 00 00 0f

而在vs這個編譯器中存儲的情況是這樣的

編譯器里默認左邊是低地址，右邊是高地址，而存儲為00 00 00 00 0f，其實是按照低字節存低地址的規則來進行的，所以是小端存儲。

代碼判斷大小端存儲

#include<stdio.h>
int check_sys()
{int i = 1;int ret = (*(char*)&i);//先把i的地址轉變為char*，然后解引用會得到內存中存儲的十六進制字節序return ret;//char *只能一個字節一個字節訪問，此時訪問的是第一個內存中的字節
}
int main()
{int ret = check_sys();if (ret == 1)//小端存儲低字節存低位{printf("小端\n");}else{printf("大端\n");}return 0;
}

整型提升

#include<stdio.h>
int main()
{unsigned char a = 200;unsigned char b = 100;unsigned char c = 0;c = a + b;printf("%d %d", a + b, c);return 0;}

為什么這代碼結果會不一樣呢，這就涉及到了整型提升

C語?中整型算術運算總是?少以缺省整型類型的精度來進?的。
為了獲得這個精度，表達式中的字符和短整型操作數在使?之前被轉換為普通整型，這種轉換稱為整型提升。

整型提升的意義

表達式的整型運算要在CPU的相應運算器件內執?，CPU內整型運算器(ALU)的操作數的字節?度?
般就是int的字節?度，同時也是CPU的通?寄存器的?度。?
因此，即使兩個char類型的相加，在CPU執?時實際上也要先轉換為CPU內整型操作數的標準?
度。
通?CPU（general-purpose CPU）是難以直接實現兩個8?特字節直接相加運算（雖然機器指令中可能有這種字節相加指令）。所以，表達式中各種?度可能?于int?度的整型值，都必須先轉換為int或unsigned int，然后才能送?CPU去執?運算。

再回到上面那個代碼

c=a+b

a里面放的是200，200的原碼本來應該是32位的00000000 00000000 00000000 11001000

?正數原反補碼相同都為00000000 00000000 00000000 11001000

放進只有8位的容器char中，發生截斷就為1100 1000

b里面放的是100，100的原碼本來應該是00000000 00000000 00000000 01100100

?正數原反補碼相同都為00000000 00000000 00000000 01100100

放進只有8位的容器char中，發生截斷就為0110 0100

b+c直接相加為100101100，這個得到的是補碼

此時以%d（32位有符號十進制原碼）打印，要先把b+c補碼的結果先填滿為32位，00000000 00000000 00000001?00101100，然后再轉換為原碼，此時最高位為0默認為正數，原反補碼都相同，所以補碼也為00000000 00000000 00000001?00101100，轉換為十進制為300，所以最后打印為300

再來考慮c=a+b，八位a和八位b直接相加為100101100，這是九位，要強行放進只有八位的容器c當中，所以會發生截斷，最高位1會被截斷了。所以c補碼最后為00101100

現在要以%d（32位有符號十進制原碼）打印，要先把c的補碼填滿為32位，00000000 00000000 00000000 00101100，正數轉原碼為000000000 00000000 00000000 00101100，轉換為十進制為44，所以結果為44.

有符號的例子

#include<stdio.h>
int main()
{char a;char b = 1;char c = -1;a = b + c;printf("%d %d", b+c, a);
}

結果是一樣的，但是先別急，試著用上面的方法來分析一下

-1的原碼為10000000 00000000 00000000 00000001

-1的反碼為11111111 11111111 11111111 11111110

-1的補碼為11111111 11111111 11111111 11111111

1的原碼是00000000 00000000 00000000 00000001

這是32位整型的情況，而char類型只能放8位，所以就會發生截斷，char c實際存放的是11111111

1是正數，原反補碼都一樣，都為00000000 00000000 00000000 00000001

這是32位整型的情況，而char類型只能放8位，所以就會發生截斷，char b實際存放的是00000001

b+c直接以十進制原碼的情況打印出來，所以b和c都要重新填滿32位然后相加，這時候要去考慮有符號或者無符號數的情況：無符號數整型提升（填滿32位），高位全補0；有符號數用符號位填滿剩下的位數。

b為有符號數，補碼正數符號位0填滿為00000000 00000000 00000000 00000001

c為有符號負數，補碼符號位1填滿為11111111 11111111 11111111 11111111

補碼直接相加為 100000000 00000000 00000000 00000000，是33位，%d打印要求32位整型打印，所以依舊會截斷，最高位1截斷了，得00000000 00000000 00000000 00000000，此時這得到的是補碼，而此時最高位為0，所以是正數，正數原反補碼相同，最后十進制打印就為0;

再來考慮一下a=b+c打印的情況，如上面說的char b實際存的是8位00000001，char c存的是8位11111111，直接b+c為100000000，九位數要放進只有8位的char a容器里，直接最高位截斷了，即得a=b+c=00000000

?而此時要把a以十進制原碼打印出來，a不足32位，所以要填滿32位，a為有符號數，最高符號位位為0，補滿32位為00000000 00000000 00000000 00000000，最高位為0默認為正數，所以原碼十進制為0，最后打印也為0；

無符號有符號整型提升串用的例子

#include<stdio.h>
int main()
{char a = -1;signed char b = -1;unsigned char c = -1;printf("a=%d,b=%d,c=%d", a, b, c);
}

同樣的分析方式，a,b為有符號數，c為無符號數，打印結果為有符號十進制整型，%u是打印十進制無符號整型

-1的原碼為10000000 00000000 00000000 00000001

-1的反碼為11111111 11111111 11111111 11111110

-1的補碼為11111111 11111111 11111111 11111111

而char a只能放8位，所以實際char a補碼放的是11111111。此時要求輸出十二位十進制原碼，所以a需要整型提升填滿，a是有符號數，此時最高位為1，補碼填滿為11111111 11111111 11111111 11111111，原碼為10000000 00000000 00000000 00000001（符號位不變其余位取反加一），轉換成十進制輸出就是-1。

b同a一樣，也是-1。

而char c補碼實際存放的是11111111，c是無符號數，無符號數整型提升填滿32位是高位全補0，即為00000000 00000000 00000000 11111111，此時最高位為0，要求打印%d類型的數據，會自動把c的最高位認為符號位，正數原反補碼相同，所以原碼為00000000 00000000 00000000 11111111，轉換成十進制打印就是255.

有符號char和無符號char范圍

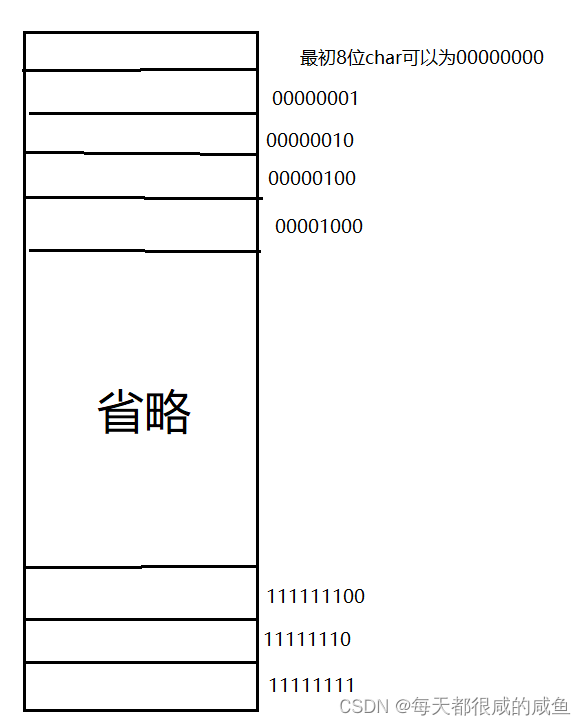
無符號char最高位為有效位，最高位參與計算，所以范圍為0到255（二進制為1111 1111）

也許有人疑惑，1000 0000反碼不是1111 1111，加1原碼為9位，截斷一位應該為1000 0000啊，最高位為-1，結果不應該為-0嗎

雖然8位二進制中，存在-0（1000 0000）和0（0000 0000），實際生活中0又沒有正負的，-0不也是0嗎，但是它卻有兩種補碼表示，。為了將補碼與數字一一對應起來，就認為把原碼-0的補碼強行人為表示為-128，所以八位二進制-128是沒有反碼和原碼的。看見補碼1000 0000，不用去按照負數求原碼規則取反加一去計算，它直接表示就是-128，這是人為規定的規則

總結有符號char 的范圍為-128到127

如果有符號數最大的正數數127（0111 1111）再加上1，會得到-128（1000 0000），而最大的負數-1（1111 1111）再加1其實得到0000 0000，形成一個環形

同樣無符號數最大的數255加1就得到最小的數0，其實也是個環形

練習

#include<stdio.h>
int main()
{char a = -128;printf("%u\n", a);return 0;
}

32位-128，原碼10000000 00000000 00000000 100000000

反碼為11111111 1111111 1111111 01111111

原碼為11111111 11111111 11111111 10000000

char a是個8位的容器，32位放進去會截斷1000 0000，而接下來要以32無符號整型輸出，8位數要重新填滿32位，即為11111111 11111111 11111111 10000000，要以無符號數十進制輸出，所以最高位1不是符號數，也要參與轉換計算。即為4294967168

二.浮點數在內存中的存儲

IEEE754標準

根據IEEE（國際電氣和電子工程協會）754標準，任意一個浮點數可以寫成下面的形式

十進制的浮點數5.0，寫成二進制為101.0，相當于1.01 x 2^2

按照上面的格式，可得s=0，m=1.01，E=2；

IEEE754規定
對于32位的浮點數，最?的1位存儲符號位S，接著的8位存儲指數E，剩下的23位存儲有效數字M

對于64位的浮點數，最?的1位存儲符號位S，接著的11位存儲指數E，剩下的52位存儲有效數字M

浮點數存的過程

IEEE754對有效數字M和指數E，還有?些特別規定。
前?說過M可以寫成 1.xxxxxx 的形式，其中 xxxxxx 表??數部分。IEEE754規定，在計算機內部保存M時，默認這個數的第?位總是1，因此可以被舍去，只保存后?的xxxxxx部分。?如保存1.01的時候，只保存01，等到讀取的時候，再把第?位的1加上去。這樣做的?的，是節省1位有效數字。以32位浮點數為例，留給M只有23位，將第?位的1舍去以后，等于可以保存24位有效數字。
?于指數E，情況就?較復雜?先，E為?個?符號整數（unsigned int）這意味著，如果E為8位，它的取值范圍為0~255；如果E為11位，它的取值范圍為0~2047。但是，我們知道，科學計數法中的E是可以出現負數的，所以IEEE754規定，存?內存時E的真實值必須再加上?個中間數，對于8位的E，這個中間數是127；對于11位的E，這個中間數是1023。?如，2^10的E是 10，所以保存成32位浮點數時，必須保存成10+127=137，即10001001。

舉個存儲的例子

0.5存儲，二進制為0.1，規定正數部分必須為1，所以右移操作得1.0*2^(-1),這是正數所以s=0，

E的存儲要加127（1023），-1+127=126，二進制表示為0111 1110.

此時M為1.0，按照規則要舍去1，只保留0，而M要存23位，bu'qi為

浮點數取的過程
?

浮點數取的過的過程可以分為三種情況

E的表示不全為0或者不全為1，這也是最常見的情況

這是浮點數取出E的規則是E的計算值減去127（或者1023），就是把前面存的時候加上的中間數減去，還原原數

E全為0的情況

這時，浮點數指數E等于1-127（或者1-1023）即為真實值，有效數字M不再加上第一位的1，而是還原為0.xxxxxx的小數。這樣是為了表示+-0，以及接近0的很小的數字

E全為1的情況

這時，如果有效數字M全為0，表示+-無窮大（正負取決于符號位s）

相關浮點數存儲的例題

#include <stdio.h>
int main()
{int n = 5;float* p= (float*)&n;printf("n的值為:%d\n", n);printf("p的值為:%f\n", *p);*p = 5.0;printf("num的值為;%d\n", n);printf("*p的值為;%f\n", *p);
}