一、題目大意

我們有N只貓，每次循環進行K次操作（N<=100，K<=100），每次操作可有以下三種選擇：

1、g i 給第i只貓1個食物

2、e i 讓第i只貓吃完它所有的食物

3、s i j 交換第i和j只貓的食物。

求出M次循環后，每只貓有多少個食物？（M<=1000000000）

二、解題思路

假設已經循環過?w 次，設第i只貓的食物數量為 ai

設循環過 w+1 次，第?i 只貓的食物數量為 bi。

不難1次循環的k個操作后，bi = a1 * m1 + a2 * m2 + a3 * m3 + ... an * mn + C

所以可推出以下的矩陣成立

同時當 ai 和 bi 之間相差M次循環時，也有如下表達式成立。

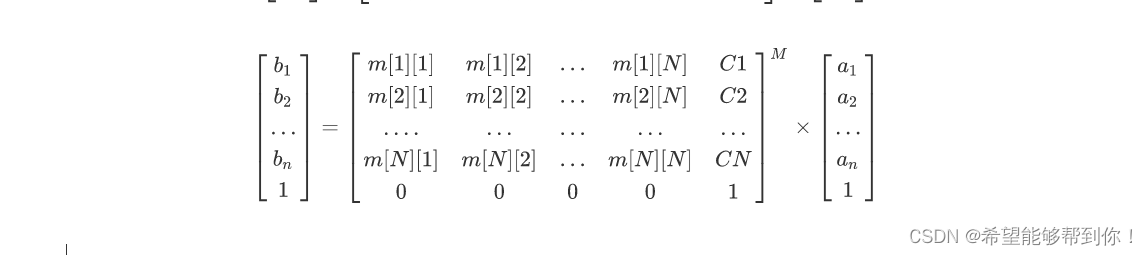
考慮下初始的情況，一開始每只貓都沒有食物，設 Si 為 M次循環后第 i 只貓的數量，把初值代入 a1 .. an，有如下表達式成立。

但是這樣我們需要使用 101 * 101大小的矩陣進行相乘，而且本題目需要開long long。

但經過思考，發現可以把矩陣降低一維成為100。

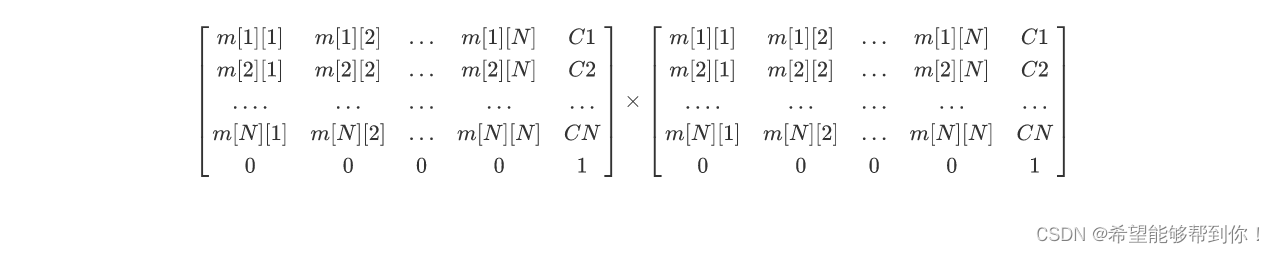
我們可以發現矩陣M次方的規律。

1、 對于矩陣中?1 <= 1?<= N，我們發現 這些值不管成多少次，都與第M+1行和N+1列無關。

2、最后一行始終不變。

3、對于最后一列，我們發現它可以通過如下表

達式。在100 * 100的復雜性內計算。

設進行經過i次循環的最后一列為Ci。對于最后一列的第 j?行則有如下表達式。

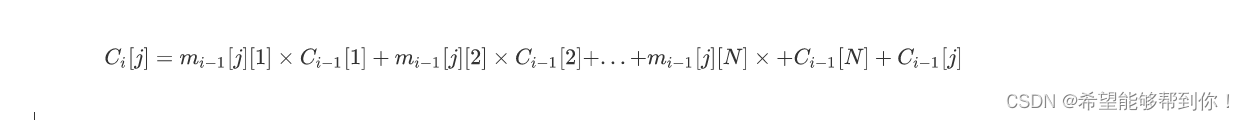
維護4個滑動數組，計算每一次更新內圈的后，再更新最后一列的值，M次操作后，最后一列的值就是答案，因為M次次冪即可求解答案。（初始時每只小鼠沒有食物，最一列開long long，中間開int即可）。

三、代碼

#include <iostream>
#include <vector>
using namespace std;
typedef long long ll;
int P[2][107][107], B[107][107];
ll _P[2][107], _B[107];
int N, M, K;
void pow(int _N)
{int cnt = 0;while (_N > 0){int crt = cnt & 1, nxt = !(cnt & 1);if (_N & 1){for (int i = 0; i < N; i++){_P[nxt][i] = _B[i];for (int j = 0; j < N; j++){_P[nxt][i] = _P[nxt][i] + ((ll)B[i][j]) * _P[crt][j];P[nxt][i][j] = 0;for (int k = 0; k < N; k++){P[nxt][i][j] = P[nxt][i][j] + B[i][k] * P[crt][k][j];}}}for (int i = 0; i < N; i++){_B[i] = _P[nxt][i];for (int j = 0; j < N; j++){B[i][j] = P[nxt][i][j];}}}for (int i = 0; i < N; i++){_P[nxt][i] = _P[crt][i];for (int j = 0; j < N; j++){_P[nxt][i] = _P[nxt][i] + ((ll)P[crt][i][j]) * _P[crt][j];P[nxt][i][j] = 0;for (int k = 0; k < N; k++){P[nxt][i][j] = P[nxt][i][j] + P[crt][i][k] * P[crt][k][j];}}}cnt++;_N >>= 1;}
}
void solve()
{for (int i = 0; i < 101; i++){for (int j = 0; j < 101; j++){B[i][j] = P[0][i][j] = P[1][i][j] = 0;}B[i][i] = 1;P[0][i][i] = 1;_P[0][i] = 0;_B[i] = 0;}char c;int a, b;for (int i = 0; i < K; i++){scanf("\n%c", &c);if (c == 'g'){scanf("%d", &a);_P[0][a - 1]++;}else if (c == 's'){scanf("%d%d", &a, &b);for (int j = 0; j < N; j++){int tmp = P[0][a - 1][j];P[0][a - 1][j] = P[0][b - 1][j];P[0][b - 1][j] = tmp;}ll tmpL = _P[0][a - 1];_P[0][a - 1] = _P[0][b - 1];_P[0][b - 1] = tmpL;}else if (c == 'e'){scanf("%d", &a);for (int j = 0; j < N; j++){P[0][a - 1][j] = 0;}_P[0][a - 1] = 0;}}pow(M);for (int i = 0; i < N; i++){printf("%lld%c", _B[i], i + 1 == N ? '\n' : ' ');}
}
int main()
{while (true){scanf("%d%d%d", &N, &M, &K);if (N == 0 && M == 0 && K == 0){break;}solve();}return 0;
}