今天看一個在深度學習中很枯燥但很重要的概念——交叉熵損失函數。
作為一種損失函數,它的重要作用便是可以將“預測值”和“真實值(標簽)”進行對比,從而輸出 loss 值,直到? loss 值收斂,可以認為神經網絡模型訓練完成。
那么這個所謂的“交叉熵”到底是什么,為什么它可以用來作為損失函數呢?
1、熵與交叉熵
“交叉熵”包含了“交叉”和“熵”這兩部分。
關于“熵”的描述在理解熵的本質一文中有更詳細的說明。總的來說,熵可以用來衡量一個隨機變量的不確定性,數學上可表示為:
H(i)?= -?∑?P(i) * log(P(i))
對于上面的公式,我們稍微變一下形,將負號和 log(P(i)) 看做一個變量,得到:
PP(i)?= -log(p(i))
那么熵的公式就可以寫作:H(i) =?∑?P(i) * PP(i)
此時熵的公式中,P(i) 和 PP(i) 是服從相同的概率分布。因此,熵H(i)就變成了事件?PP(i) 發生的數學期望,通俗理解為均值。
熵越大,表示事件發生的不確定性越大。而交叉熵是用于比較兩個概率分布之間的差異,對于兩個概率分布 P 和 Q?而言,
交叉熵定義為:
H(i)?=?∑?P(i) * Q(i)
此時,P(i) 和 Q(i) 服從兩種不同的概率分布,交叉熵的“交叉”就體現在這。
其中 P(i) 為真實分布,也就是訓練過程中標簽的分布;Q(i) 為預測分布,也就是模型每輪迭代輸出的預測結果的分布。
交叉熵越小,表示兩個概率分布越接近。
從而模型預測結果就越接近真實標簽結果,說明模型訓練收斂了。
關于更細節的數學原理,可以查看熵的本質,不過我們也可以不用深究,理解上述結論就可以。
2、交叉熵作為損失函數
假設有一個動物圖像數據集,其中有五種不同的動物,每張圖像中只有一只動物。

來源:https:?//www.freeimages.com/
我們將每張圖像都使用 one-hot 編碼來標記動物。對one-hot編碼不清楚的可以移步這里有個你肯定能理解的one-hot。

上圖是對動物分類進行編碼后的表格,我們可以將一個one-hot 編碼視為每個圖像的概率分布,那么:
第一個圖像是狗的概率分布是 1.0 (100%)。

對于第二張圖是狐貍的概率分布是1.0(100%)。

以此類推,此時,每個圖像的熵都為零。
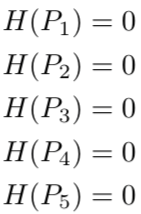
換句話說,one-hot 編碼標簽 100% 確定地告訴我們每張圖像有哪些動物:第一張圖片不可能 90% 是狗,10% 是貓,因為它100%是狗。
因為這是訓練的標簽,是固定下來的確定分布。
現在,假設有一個神經網絡模型來對這些圖像進行預測,在神經網絡執行完一輪訓練迭代后,它可能會對第一張圖像(狗)進行如下分類:
![]()
該分類表明,第一張圖像越 40%的概率是狗,30%的概率是狐貍,5%的概率是馬,5%的概率是老鷹,20%的概率是松鼠。
但是,單從圖像標簽上看,它100%是一只狗,標簽為我們提供了這張圖片的準確的概率分布。
![]()
那么,此時如何評價模型預測的效果呢?
我們可以計算利用標簽的one-hot編碼作為真實概率分布 P,模型預測的結果作為 Q 來計算交叉熵:

結果明顯高于標簽的零熵,說明預測結果并不是很好。
繼續看另一個例子。
假設模型經過了改良,在完成一次推理或者一輪訓練后,對第一張圖得到了如下的預測,也就是說這張圖有98%的概率是狗,這個標簽的100%已經差的很少了。
![]()
我們依然計算交叉熵:

可以看到交叉熵變得很低,隨著預測變得越來越準確,交叉熵會下降,如果預測是完美的,它就會變為零。
基于此理論,很多分類模型都會利用交叉熵作為模型的損失函數。
在機器學習中,由于多種原因(比如更容易計算導數),對數 log 的計算大部分情況下是使用基數 e 而不是基數 2 ,對數底的改變不會引起任何問題,因為它只改變幅度。
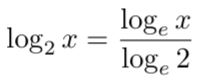


(快速排序(1)))





)




 uniapp微信小程序)



)
:RK3568底板電路VGA顯示接口原理圖分析)
