目錄

一、復雜網絡建模

二、圖嵌入方法（Graph Convolutional Networks (GCN) ）

1. 圖表示：

2. 鄰接矩陣（Adjacency Matrix）：

3. 圖卷積層（Graph Convolutional Layer）：

4. 激活函數和損失函數：

5. 訓練過程：

6. 應用：

三、基于PyTorch的GCN實現的示例代碼

---

一、復雜網絡建模

復雜網絡是一種由大量相互連接的元素（節點或頂點）組成的網絡結構，這些連接通常是非常復雜和動態的。這些網絡可以在各種領域中發現，包括社交網絡、生物學系統、信息技術和交通系統等。

復雜網絡的研究主要關注網絡的拓撲結構、動力學行為和功能性質。其中一些常見的復雜網絡模型包括小世界網絡、無標度網絡和隨機網絡。這些模型幫助我們理解網絡中信息傳播、穩定性、魯棒性等方面的特性。

在實際應用中，復雜網絡理論被用于解決許多問題，例如社交網絡分析、疾病傳播模型、電力系統優化等。這個領域的研究對于理解現實世界中復雜系統的行為具有重要意義。

復雜網絡的建模方法多種多樣，因取決于網絡的性質、應用領域和研究問題。以下是一些常見的復雜網絡建模方法：

1. 隨機圖模型（Random Graph Models）： 這包括 Erd?s-Rényi 模型、Gilbert 模型等，其中節點之間的連接是隨機生成的。這些模型通常用于研究網絡的基本性質。

2. 小世界網絡模型（Small-World Models）： Watts-Strogatz 模型是一個著名的小世界網絡模型，它通過添加隨機連接來模擬現實中的短路徑和高聚集性。

3. 無標度網絡模型（Scale-Free Models）： Barabási-Albert 模型是一個常見的無標度網絡模型，其中網絡的度分布遵循冪律分布。這種模型更好地捕捉了現實中一些節點擁有更多連接的現象，也就是所謂的“富者愈富”。

4. 演化網絡模型（Evolutionary Models）： 這些模型考慮網絡隨時間演變的過程，包括節點的加入和離開，連接的形成和斷裂。Leskovec 的 Preferential Attachment with Fitness Model 就是一個演化網絡的例子。

5. 時空網絡模型（Spacetime Networks Models）： 考慮網絡隨時間和空間的變化，尤其在交通流、移動網絡等領域有應用。

6. 復雜系統動力學模型： 使用微分方程、差分方程或代數方程等來描述網絡中節點和連接的動力學行為。這類模型通常用于研究網絡的穩定性、同步現象等。

7. 社會網絡建模方法： 在社會網絡中，可以使用Agent-Based Modeling（基于代理的建模）等方法來考慮個體行為和相互作用，以更真實地模擬社交網絡的演化。

8. 復雜網絡在具體領域的應用模型： 例如生物網絡模型、交通網絡模型、腦網絡模型等。這些模型針對具體領域的特點進行了調整和拓展。

二、圖嵌入方法（Graph Convolutional Networks (GCN) ）

1. 圖嵌入（Graph Embedding）：

   • 定義： 圖嵌入是將圖中的節點或邊映射到低維向量空間的過程。目標是在低維空間中保留圖的結構信息，使得相鄰節點或邊在向量空間中更接近。
   • 應用： 圖嵌入可用于各種任務，如節點分類、節點聚類、圖分類、鏈接預測等。常見的圖嵌入方法包括DeepWalk、node2vec、GraphSAGE等。

2. 圖自編碼器（Graph Autoencoder）：

   • 定義： 圖自編碼器是一種神經網絡結構，用于學習圖的表示。它包括一個編碼器和一個解碼器，通過訓練網絡，使得輸入圖被映射到一個低維表示，同時盡量保留圖的結構信息。
   • 應用： 圖自編碼器常用于無監督學習任務，如圖的重構、降維、異常檢測等。它們可以通過最小化重構誤差來學習有效的圖表示。Variational Graph Autoencoder (VGAE) 是圖自編碼器的一種變體，引入了變分推斷的思想。

區別總結：

• 圖嵌入是一個更廣泛的概念，描述了將圖中的元素映射到低維空間的過程，而不限定于具體的學習方法。
• 圖自編碼器是一種特定類型的神經網絡結構，用于學習圖的表示，通常通過編碼器和解碼器的結構來實現。

雖然圖自編碼器可以用于圖嵌入，但圖嵌入方法不一定都基于自編碼器結構，也可能采用其他技術和模型。

通過圖嵌入，你可以獲得每個節點或邊的低維表示，這些表示在向量空間中保留了網絡的結構信息。這樣的表示可以用于多種任務，例如：

1. 節點分類： 將節點映射到低維空間后，可以在該空間中執行節點分類任務，例如確定節點所屬的類別或標簽。

2. 鏈接預測： 通過節點之間的低維表示，可以預測網絡中可能存在的鏈接或邊。

3. 圖分類： 將整個圖映射到低維空間，使得圖的結構信息得以保留，可以用于圖分類任務，例如判斷圖的類型或屬性。

4. 可視化： 通過在低維空間中表示網絡，可以將網絡結構可視化，幫助理解網絡的拓撲結構。

圖嵌入的方法包括諸如 DeepWalk、node2vec、GraphSAGE、Graph Convolutional Networks (GCN) 等。這些方法可以應用于不同類型的網絡數據，包括社交網絡、生物網絡、知識圖譜等。

Graph Convolutional Networks (GCN) 是一種用于圖結構數據的深度學習模型，最早由Kipf和Welling于2017年提出。GCN的目標是學習節點在圖中的表示，使得節點的表示能夠捕捉其鄰居節點的信息，從而有效地處理圖結構的任務，如節點分類、圖分類、鏈路預測等。

以下是GCN的基本原理和關鍵概念：

1. 圖表示：

• 節點表示： 圖中的每個節點表示一個實體，可以是用戶、物品、論文等。

• 邊表示： 圖中的邊表示節點之間的關系，可以是有向邊或無向邊。

2. 鄰接矩陣（Adjacency Matrix）：

• GCN使用鄰接矩陣來表示圖的拓撲結構。對于圖 (G)，鄰接矩陣 (A) 的元素 (A_{ij}) 表示節點 (i) 和節點 (j) 之間是否存在邊。

3. 圖卷積層（Graph Convolutional Layer）：

• 圖卷積操作： GCN通過圖卷積操作來更新節點的表示。一個單層GCN的更新規則可以表示為 (H' = f(\hat{D}^{-\frac{1}{2}}\hat{A}\hat{D}^{-\frac{1}{2}}XW))，其中 (H') 是更新后的節點表示，(\hat{A}) 是對稱歸一化的鄰接矩陣，(\hat{D}) 是對角度矩陣，(X) 是節點特征矩陣，(W) 是權重矩陣，(f) 是激活函數。

• 多層GCN： 多層GCN模型通過堆疊多個圖卷積層，逐漸聚合更多的上下文信息，提高節點表示的表達能力。

4. 激活函數和損失函數：

• 激活函數： 通常使用ReLU等激活函數。

• 損失函數： 對于監督學習任務，如節點分類，通常使用交叉熵損失函數。

5. 訓練過程：

• 通過已知的節點標簽進行監督學習。通過反向傳播和梯度下降等優化算法，迭代地更新模型的參數。

6. 應用：

• GCN廣泛應用于圖結構數據的任務，如社交網絡分析、生物信息學、知識圖譜等。

GCN的提出填補了傳統卷積神經網絡（CNN）在處理圖結構數據上的不足，使得深度學習模型能夠更好地理解和利用圖數據的結構信息。雖然GCN是一種成功的模型，但后續也出現了一些改進版本，如GraphSAGE、GAT（Graph Attention Network）等，以應對不同類型的圖數據和任務。

三、基于PyTorch的GCN實現的示例代碼

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optimclass GraphConvolutionLayer(nn.Module):def __init__(self, input_dim, output_dim):super(GraphConvolutionLayer, self).__init__()self.linear = nn.Linear(input_dim, output_dim)def forward(self, adjacency_matrix, node_features):# 對鄰接矩陣進行對稱歸一化row_sum = adjacency_matrix.sum(1, keepdim=True)normalized_adjacency = adjacency_matrix / row_sum# 執行圖卷積操作result = torch.matmul(normalized_adjacency, node_features)result = self.linear(result)result = F.relu(result)return resultclass GCN(nn.Module):def __init__(self, input_dim, hidden_dim, output_dim):super(GCN, self).__init__()self.gc1 = GraphConvolutionLayer(input_dim, hidden_dim)self.gc2 = GraphConvolutionLayer(hidden_dim, output_dim)def forward(self, adjacency_matrix, node_features):h1 = self.gc1(adjacency_matrix, node_features)h2 = self.gc2(adjacency_matrix, h1)return h2# 示例數據
# 假設有一個簡單的無向圖，鄰接矩陣表示為：
# adjacency_matrix = [[0, 1, 1],
#                    [1, 0, 1],
#                    [1, 1, 0]]
adjacency_matrix = torch.tensor([[0, 1, 1],[1, 0, 1],[1, 1, 0]], dtype=torch.float32)# 假設每個節點有一個特征，表示為：
# node_features = [[1, 2],
#                  [3, 4],
#                  [5, 6]]
node_features = torch.tensor([[1, 2],[3, 4],[5, 6]], dtype=torch.float32)# 創建GCN模型
input_dim = node_features.size(1)
hidden_dim = 16
output_dim = 2
gcn_model = GCN(input_dim, hidden_dim, output_dim)# 模型前向傳播
output = gcn_model(adjacency_matrix, node_features)
print("GCN Output:\n", output)

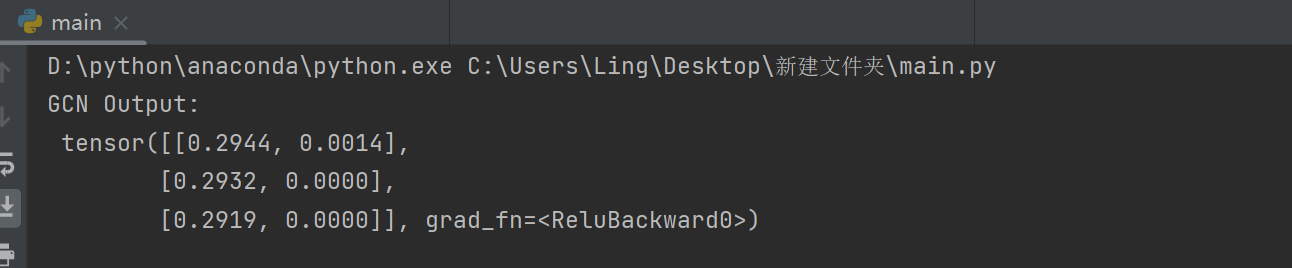?這只是一個簡單的示例，實際中可能需要根據任務和數據的不同進行更復雜的模型設計和訓練過程。此外，對于更大規模的圖數據，可能需要使用圖采樣等技術以提高訓練效率。

在GCN鏈路預測中，這可以通過以下步驟實現：

1. 生成正樣本和負樣本： 從圖中已有的邊中隨機選擇一部分作為正樣本，然后從圖中不存在的邊中隨機選擇相同數量的邊作為負樣本。

2. 定義損失函數： 使用二元交叉熵損失函數，對模型輸出的概率進行損失計算。

3. 訓練模型： 使用已有的正樣本和負樣本進行監督學習，迭代地更新模型的參數。

import torch
import torch.nn as nn
import dgl
import dgl.function as fn
import torch.optim as optim
from sklearn.metrics import roc_auc_score
from sklearn.model_selection import train_test_split# 構建一個簡單的GCN模型
class GCN(nn.Module):def __init__(self, in_feats, hidden_size, out_feats):super(GCN, self).__init__()self.layer1 = GraphConvolution(in_feats, hidden_size)self.layer2 = GraphConvolution(hidden_size, out_feats)def forward(self, g, features):x = torch.relu(self.layer1(g, features))x = self.layer2(g, x)return x# 圖卷積層的定義
class GraphConvolution(nn.Module):def __init__(self, in_feats, out_feats):super(GraphConvolution, self).__init__()self.linear = nn.Linear(in_feats, out_feats)def forward(self, g, features):with g.local_scope():g.ndata['h'] = featuresg.update_all(fn.copy_src(src='h', out='m'),fn.sum(msg='m', out='h_neigh'))h_neigh = g.ndata['h_neigh']return self.linear(h_neigh)# 數據加載和預處理
# 這里假設你有一個鄰接矩陣`adjacency_matrix`和節點特征矩陣`features_matrix`，以及一個標簽向量`labels`
# 請根據你的數據格式進行調整# 構建圖
graph = dgl.graph(adjacency_matrix)
features = torch.tensor(features_matrix, dtype=torch.float32)
labels = torch.tensor(labels, dtype=torch.float32)# 劃分訓練集和測試集
train_mask, test_mask = train_test_split(range(len(labels)), test_size=0.2, random_state=42)# 初始化模型、損失函數和優化器
model = GCN(features.shape[1], 16, 1)
criterion = nn.BCEWithLogitsLoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)# 訓練模型
for epoch in range(100):model.train()logits = model(graph, features)loss = criterion(logits[train_mask], labels[train_mask].view(-1, 1))optimizer.zero_grad()loss.backward()optimizer.step()# 計算AUCwith torch.no_grad():model.eval()pred_probs = torch.sigmoid(logits[test_mask]).numpy()auc = roc_auc_score(labels[test_mask].numpy(), pred_probs)print(f'Epoch {epoch + 1}, Loss: {loss.item():.4f}, AUC: {auc:.4f}')# 鏈路預測結果
model.eval()
logits = model(graph, features)
pred_probs = torch.sigmoid(logits).detach().numpy()

?關于復雜網絡建模，我前面寫了很多，大家可以學習參考。

【復雜網絡建模】——常用繪圖軟件和庫_圖論畫圖軟件

【復雜網絡建模】——Pytmnet進行多層網絡分析與可視化

【復雜網絡建模】——Python通過平均度和隨機概率構建ER網絡

【復雜網絡建模】——通過圖神經網絡來建模分析復雜網絡

【復雜網絡建模】——Python可視化重要節點識別(PageRank算法)

【復雜網絡建模】——基于Pytorch構建圖注意力網絡模型

【復雜網絡建模】——Hypergraphx: 用于高階網絡分析的庫

【復雜網絡建模】——基于節點相似性的社團劃分算法

【復雜網絡建模】——鏈路預測算法及其應用

?【復雜網絡建模】——ER網絡度分布、無標度網絡度分布