---

一、插入排序

思路：

當插入第i(i>=1)個元素時，前面的array[0],array[1],…,array[i-1]已經排好序，此時用array[i]的排序碼與array[i-1],array[i-2],…的排序碼順序進行比較，找到插入位置即將array[i]插入，原來位置上的元素順序后移

如：

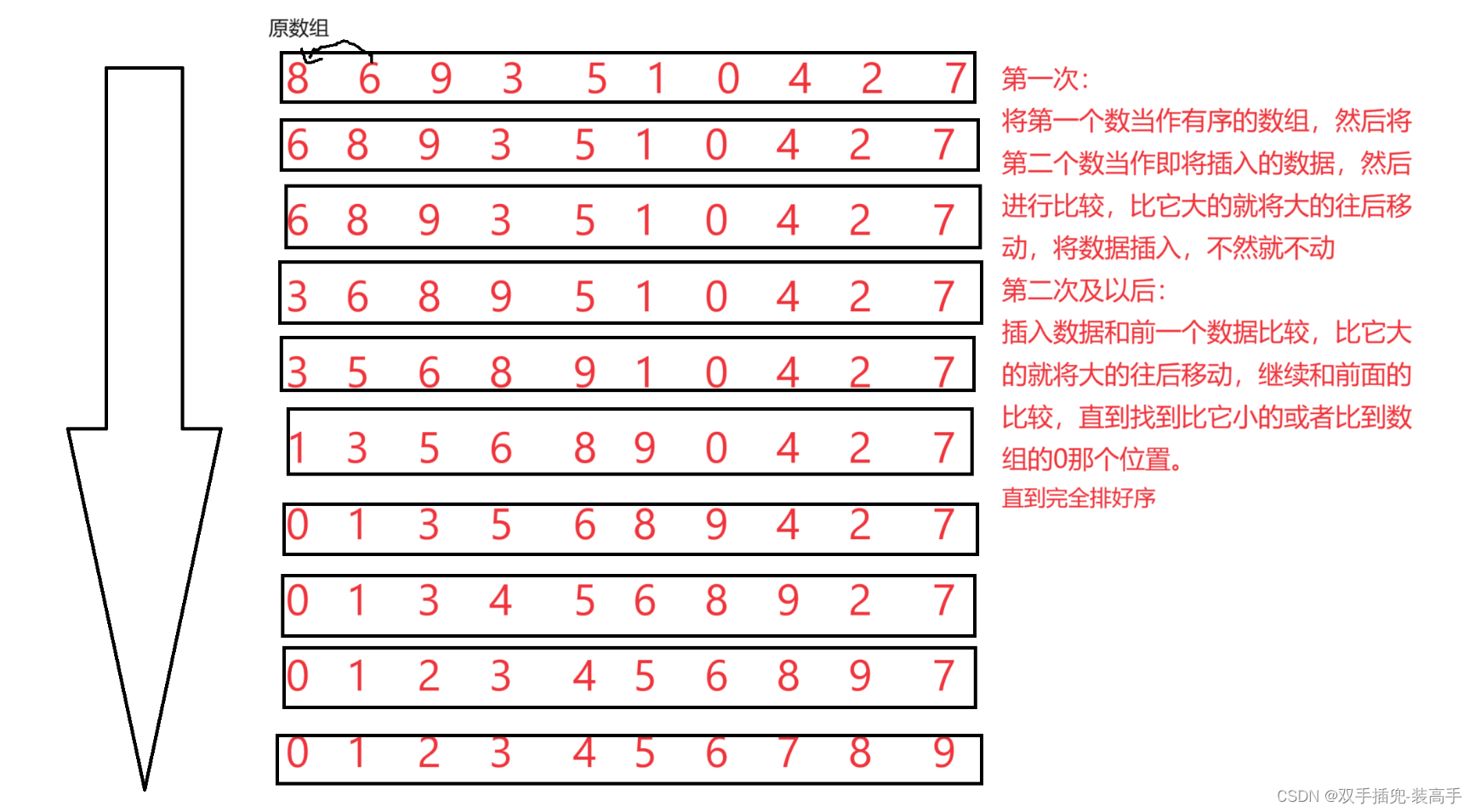
代碼實現：

void  test(int arr[],int size) {int ned ;//定義一個插入數據的前一個數據的下標for (int i = 0; i < size-1; i++) {ned = i;//從第一個開始int t = arr[ned + 1];//需要插入的數據while (ned >= 0)//當遍歷到最后一個結束{if (arr[ned] > t)//比插入數據大就插入{arr[ned + 1] = arr[ned];//往后移動一位ned--;//--找下一個數據}else//找到比t小的結束break;}arr[ned + 1] = t;//在比t小的數據前一位插入
//這樣就算那個數是最小的我，和下標為0那個位置比完后，ned=-1，
//我們也可以插入到下標為0 的位置}
}
void Print(int arr[], int size) {for (int i = 0; i < size; i++)printf("%d ", arr[i]);printf("\n");
}
int main() {int arr[] = { 8,6,9,3,5,1,0,4,2,7 };Print(arr, sizeof(arr) / sizeof(arr[0]));test(arr, sizeof(arr)/sizeof(arr[0]));Print(arr, sizeof(arr) / sizeof(arr[0]));return 0；}

運行結果：

時間復雜度：
第一層循環怎么都要走N次，第二層循環最好的結果為（已經排好序），為1次，
最壞的結果，（與想要的順序相反），為N次
我們取最壞的結果，N ^ N次，所以時間復雜度O(N^N).

二、希爾排序

思路：
1.實質上還是使用插入排序的思想
2.我們將數組的數據進行分組排序，每間隔 gap 的為一組，這些排序叫做預排序，設置多組間隔為 gap ，經過預排序的數組就會接近有序
如：

3.那么這個 gap 怎么設置呢？，我們知道，當gap=1時就是相當于直接插入排序，因此我們可以這樣設置，就是gap 由大到小，最后到1，結束
4.gap設置的特點
gap越大，大的數可以越快排到后面，小的數可以越快的排到前面，但是預排完，不是那么接近有序
gap越小 越接近有序
gap=1，就是直接插入排序
如：

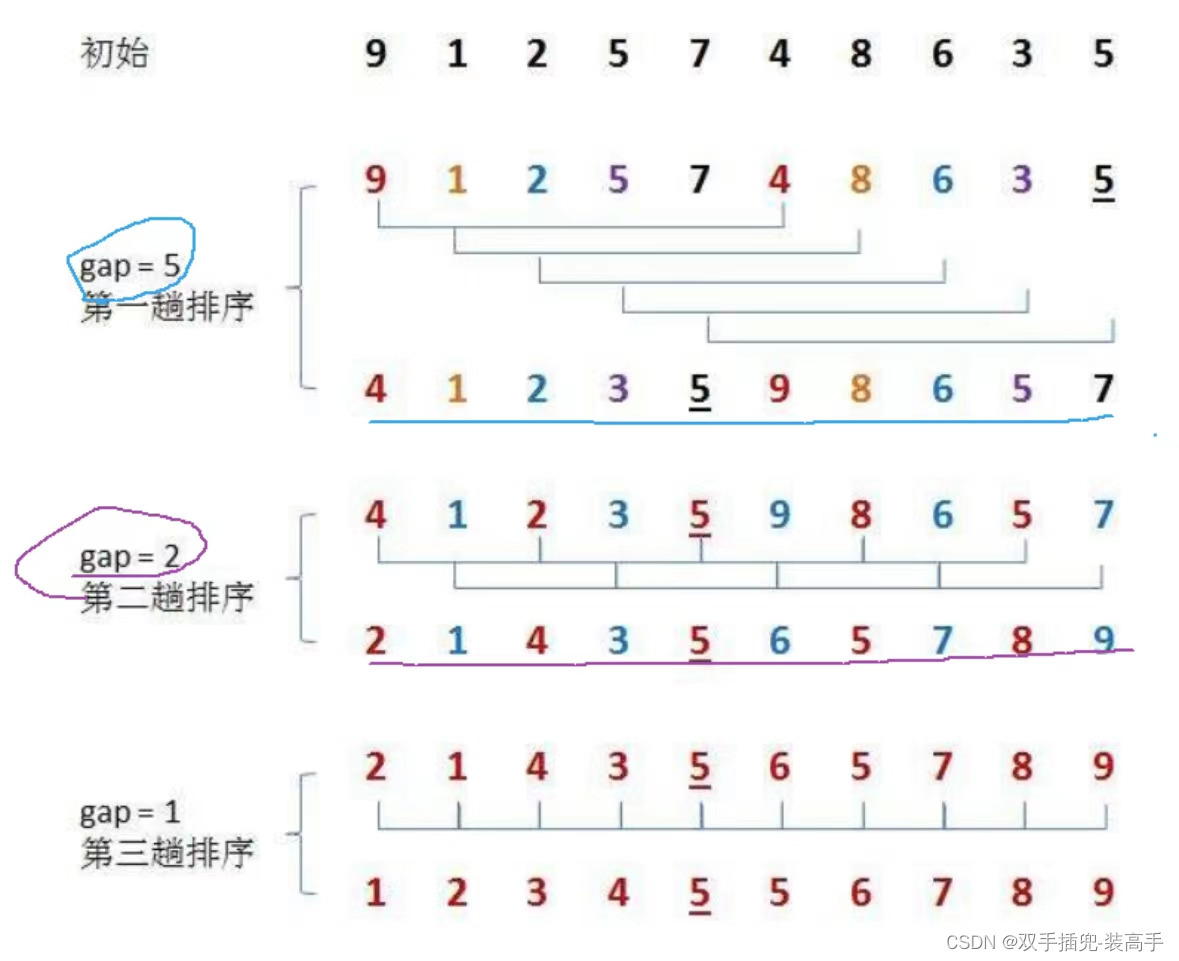
代碼實現：

void test1(int arr[], int size) {int gap = size;//設為數據的個數int ned = 0;while (gap!= 1)//結束條件；當gap=1時{gap = gap / 3 + 1;//除三或者二都可，每次都會減少，加1保證有一次gap=1//每間隔gap的數據就進行一次插入排序//結束條件：當i+gap>n時for (int i = 0; i < size - gap; i++){//以下和我們上面的插入排序一樣ned = i;int t = arr[ned + f];while (ned >= 0) {if (arr[ned] > t) {arr[ned + gap] = arr[ned];ned -= gap;}elsebreak;}arr[ned + gap] = t;}}
}
void Print(int arr[], int size) {for (int i = 0; i < size; i++)printf("%d ", arr[i]);printf("\n");
}int main() {int arr[] = { 8,6,9,3,5,1,0,4,2,7 };Print(arr, sizeof(arr) / sizeof(arr[0]));test1(arr, sizeof(arr) / sizeof(arr[0]));Print(arr, sizeof(arr) / sizeof(arr[0]));return 0;
}

運行結果：

時間復雜度：
第一次循環每次除3就是，以3為底的logN，
當gap很大時，因為循環的次數減少，所以后兩層循環的次數很接近N
當gap很小時，因為已經接近有序了，所以循環的次數也接近N
所以時間復雜度為 O(lonN*N)(以3為底的logN)
當然這只時估算的結果，不一定準確
嚴蔚敏老師他的數據結構這本書上是：O（N^1.3）

以上就是我的分享了，如果有什么錯誤，歡迎在評論區留言。
最后，謝謝大家的觀看！