YOLOv8改進 | 2023 | LSKAttention大核注意力機制助力極限漲點

論文地址：官方論文地址

代碼地址：官方代碼地址

一、本文介紹?

在這篇文章中，我們將講解如何將LSKAttention大核注意力機制應用于YOLOv8，以實現顯著的性能提升。首先，我們介紹LSKAttention機制的基本原理，它主要通過將深度卷積層的2D卷積核分解為水平和垂直1D卷積核，減少了計算復雜性和內存占用。接著，我們介紹將這一機制整合到YOLOv8的方法，以及它如何幫助提高處理大型數據集和復雜視覺任務的效率和準確性。本文還將提供代碼實現細節和使用方法，展示這種改進對目標檢測、語義分割等方面的積極影響。通過實驗YOLOv8在整合LSKAttention機制后，實現了檢測精度提升(下面會附上改進LSKAttention機制和基礎版本的結果對比圖)。

?專欄回顧：YOLOv8改進系列專欄——本專欄持續復習各種頂會內容——科研必備

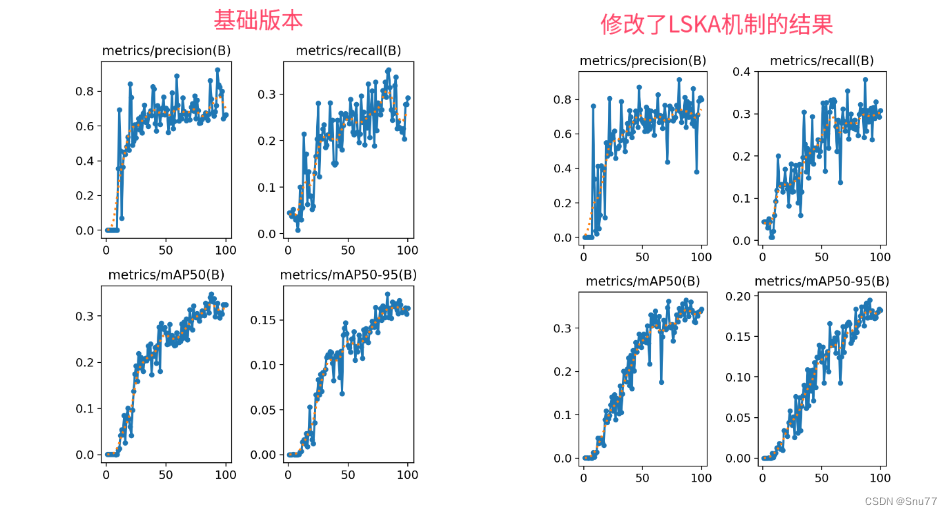
實驗效果圖如下所示->?

本次實驗我只用了一百張圖片檢測的是安全帽訓練了一百個epoch，該結果只能展示出該機制有效，但是并不能產生決定性結果，因為具體的效果還要看你的數據集和實驗環境所影響。

目錄

一、本文介紹?

二、LSKAttention的機制原理?

三、LSKAttention的代碼

四、手把手教你將LSKAttention添加到你的網絡結構中

4.1?LSKAttention的添加教程

4.2?LSKAttention的yaml文件和訓練截圖

4.2.1 LSKAttention的yaml文件

4.2.2 LSKAttention的訓練過程截圖?

五、LSKAttention可添加的位置

5.1 推薦LSKAttention可添加的位置?

5.2圖示LSKAttention可添加的位置?

六、本文總結?

二、LSKAttention的機制原理?

《Large Separable Kernel Attention》這篇論文提出的LSKAttention的機制原理是針對傳統大核注意力（Large Kernel Attention，LKA）模塊在視覺注意網絡（Visual Attention Networks，VAN）中的應用問題進行的改進。LKA模塊在處理大尺寸卷積核時面臨著高計算和內存需求的挑戰。LSKAttention通過以下幾個關鍵步驟和原理來解決這些問題：

  1. 核分解：LSKAttention的核心創新是將傳統的2D卷積核分解為兩個1D卷積核。首先，它將一個大的2D核分解成水平（橫向）和垂直（縱向）的兩個1D核。這樣的分解大幅降低了參數數量和計算復雜度。

  2. 串聯卷積操作：在進行卷積操作時，LSKAttention首先使用一個1D核對輸入進行水平方向上的卷積，然后使用另一個1D核進行垂直方向上的卷積。這兩步卷積操作串聯執行，從而實現了與原始大尺寸2D核相似的效果。

  3. 計算效率提升：由于分解后的1D卷積核大大減少了參數的數量，LSKAttention在執行時的計算效率得到顯著提升。這種方法特別適用于處理大尺寸的卷積核，能夠有效降低內存占用和計算成本。

  4. 保持效果：雖然采用了分解和串聯的策略，LSKAttention仍然能夠保持類似于原始LKA的性能。這意味著在處理圖像的關鍵特征（如邊緣、紋理和形狀）時，LSKAttention能夠有效地捕捉到重要信息。

  5. 適用于多種任務：LSKAttention不僅在圖像分類任務中表現出色，還能夠在目標檢測、語義分割等多種計算機視覺任務中有效應用，顯示出其廣泛的適用性。

總結：LSKAttention通過創新的核分解和串聯卷積策略，在降低計算和內存成本的同時，保持了高效的圖像處理能力，這在處理大尺寸核和復雜圖像數據時特別有價值。

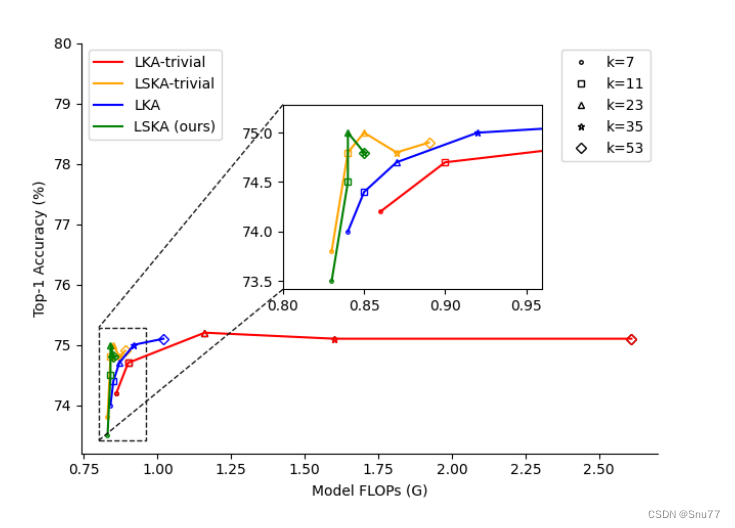
上圖展示了在不同大核分解方法和核大小下的速度-精度權衡。在這個比較中，使用了不同的標記來代表不同的核大小，并且以VAN-Tiny作為對比的模型。從圖中可以看出，LKA的樸素設計（LKA-trivial）以及在VAN中的實際設計，在核大小增加時會導致更高的GFLOPs（十億浮點運算次數）。相比之下，論文提出的LSKA（Large Separable Kernel Attention）-trivial和VAN中的LSKA在核大小增加時顯著降低了GFLOPs，同時沒有降低性能?

上圖展示了大核注意力模塊不同設計的比較，具體包括：

  1. LKA-trivial：樸素的2D大核深度卷積（DW-Conv）與1×1卷積結合（圖a）。
  2. LSKA-trivial：串聯的水平和垂直1D大核深度卷積與1×1卷積結合（圖b）。
  3. 原始LKA設計：在VAN中包括標準深度卷積（DW-Conv）、擴張深度卷積（DW-D-Conv）和1×1卷積（圖c）。
  4. 提出的LSKA設計：將LKA的前兩層分解為四層，每層由兩個1D卷積層組成（圖d）。其中，N代表Hadamard乘積，k代表最大感受野，d代表擴張率??。

個人總結：提出了一種創新的大型可分離核注意力（LSKA）模塊，用于改進卷積神經網絡（CNN）。這種模塊通過將2D卷積核分解為串聯的1D核，有效降低了計算復雜度和內存需求。LSKA模塊在保持與標準大核注意力（LKA）模塊相當的性能的同時，顯示出更高的計算效率和更小的內存占用。

三、LSKAttention的代碼

將下面的代碼在"ultralytics/nn/modules" 目錄下創建一個py文件復制粘貼進去然后按照章節四進行添加即可(需要按照有參數的注意力機制添加)。

import torch
import torch.nn as nnclass LSKA(nn.Module):def __init__(self, dim, k_size):super().__init__()self.k_size = k_sizeif k_size == 7:self.conv0h = nn.Conv2d(dim, dim, kernel_size=(1, 3), stride=(1,1), padding=(0,(3-1)//2), groups=dim)self.conv0v = nn.Conv2d(dim, dim, kernel_size=(3, 1), stride=(1,1), padding=((3-1)//2,0), groups=dim)self.conv_spatial_h = nn.Conv2d(dim, dim, kernel_size=(1, 3), stride=(1,1), padding=(0,2), groups=dim, dilation=2)self.conv_spatial_v = nn.Conv2d(dim, dim, kernel_size=(3, 1), stride=(1,1), padding=(2,0), groups=dim, dilation=2)elif k_size == 11:self.conv0h = nn.Conv2d(dim, dim, kernel_size=(1, 3), stride=(1,1), padding=(0,(3-1)//2), groups=dim)self.conv0v = nn.Conv2d(dim, dim, kernel_size=(3, 1), stride=(1,1), padding=((3-1)//2,0), groups=dim)self.conv_spatial_h = nn.Conv2d(dim, dim, kernel_size=(1, 5), stride=(1,1), padding=(0,4), groups=dim, dilation=2)self.conv_spatial_v = nn.Conv2d(dim, dim, kernel_size=(5, 1), stride=(1,1), padding=(4,0), groups=dim, dilation=2)elif k_size == 23:self.conv0h = nn.Conv2d(dim, dim, kernel_size=(1, 5), stride=(1,1), padding=(0,(5-1)//2), groups=dim)self.conv0v = nn.Conv2d(dim, dim, kernel_size=(5, 1), stride=(1,1), padding=((5-1)//2,0), groups=dim)self.conv_spatial_h = nn.Conv2d(dim, dim, kernel_size=(1, 7), stride=(1,1), padding=(0,9), groups=dim, dilation=3)self.conv_spatial_v = nn.Conv2d(dim, dim, kernel_size=(7, 1), stride=(1,1), padding=(9,0), groups=dim, dilation=3)elif k_size == 35:self.conv0h = nn.Conv2d(dim, dim, kernel_size=(1, 5), stride=(1,1), padding=(0,(5-1)//2), groups=dim)self.conv0v = nn.Conv2d(dim, dim, kernel_size=(5, 1), stride=(1,1), padding=((5-1)//2,0), groups=dim)self.conv_spatial_h = nn.Conv2d(dim, dim, kernel_size=(1, 11), stride=(1,1), padding=(0,15), groups=dim, dilation=3)self.conv_spatial_v = nn.Conv2d(dim, dim, kernel_size=(11, 1), stride=(1,1), padding=(15,0), groups=dim, dilation=3)elif k_size == 41:self.conv0h = nn.Conv2d(dim, dim, kernel_size=(1, 5), stride=(1,1), padding=(0,(5-1)//2), groups=dim)self.conv0v = nn.Conv2d(dim, dim, kernel_size=(5, 1), stride=(1,1), padding=((5-1)//2,0), groups=dim)self.conv_spatial_h = nn.Conv2d(dim, dim, kernel_size=(1, 13), stride=(1,1), padding=(0,18), groups=dim, dilation=3)self.conv_spatial_v = nn.Conv2d(dim, dim, kernel_size=(13, 1), stride=(1,1), padding=(18,0), groups=dim, dilation=3)elif k_size == 53:self.conv0h = nn.Conv2d(dim, dim, kernel_size=(1, 5), stride=(1,1), padding=(0,(5-1)//2), groups=dim)self.conv0v = nn.Conv2d(dim, dim, kernel_size=(5, 1), stride=(1,1), padding=((5-1)//2,0), groups=dim)self.conv_spatial_h = nn.Conv2d(dim, dim, kernel_size=(1, 17), stride=(1,1), padding=(0,24), groups=dim, dilation=3)self.conv_spatial_v = nn.Conv2d(dim, dim, kernel_size=(17, 1), stride=(1,1), padding=(24,0), groups=dim, dilation=3)self.conv1 = nn.Conv2d(dim, dim, 1)def forward(self, x):u = x.clone()attn = self.conv0h(x)attn = self.conv0v(attn)attn = self.conv_spatial_h(attn)attn = self.conv_spatial_v(attn)attn = self.conv1(attn)return u * attn

四、手把手教你將LSKAttention添加到你的網絡結構中

4.1?LSKAttention的添加教程

添加教程這里不再重復介紹、因為專欄內容有許多，添加過程又需要截特別圖片會導致文章大家讀者也不通順如果你已經會添加注意力機制了，可以跳過本章節，如果你還不會，大家可以看我下面的文章，里面詳細的介紹了拿到一個任意機制(C2f、Conv、Bottleneck、Loss、DetectHead)如何添加到你的網絡結構中去。

添加教程->YOLOv8改進 | 如何在網絡結構中添加注意力機制、C2f、卷積、Neck、檢測頭

需要注意的是本文的task.py配置的代碼如下(你現在不知道其是干什么用的可以看添加教程)->?

        elif m in {LSKA}:args = [ch[f], *args]

4.2?LSKAttention的yaml文件和訓練截圖

4.2.1 LSKAttention的yaml文件

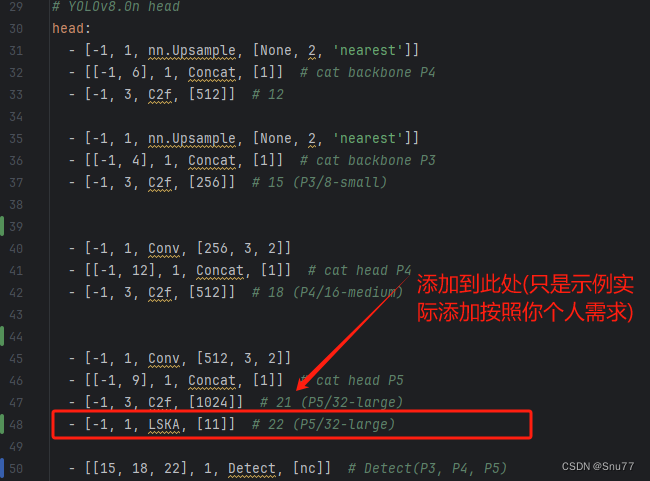
參數位置可以填寫的有7、11、23、35、41、53(代表卷積核的大小)，具體哪個效果好可能要大家自己進行一定的嘗試才可以，需要注意的是這里卷積核越大計算量就會變得越大。

?

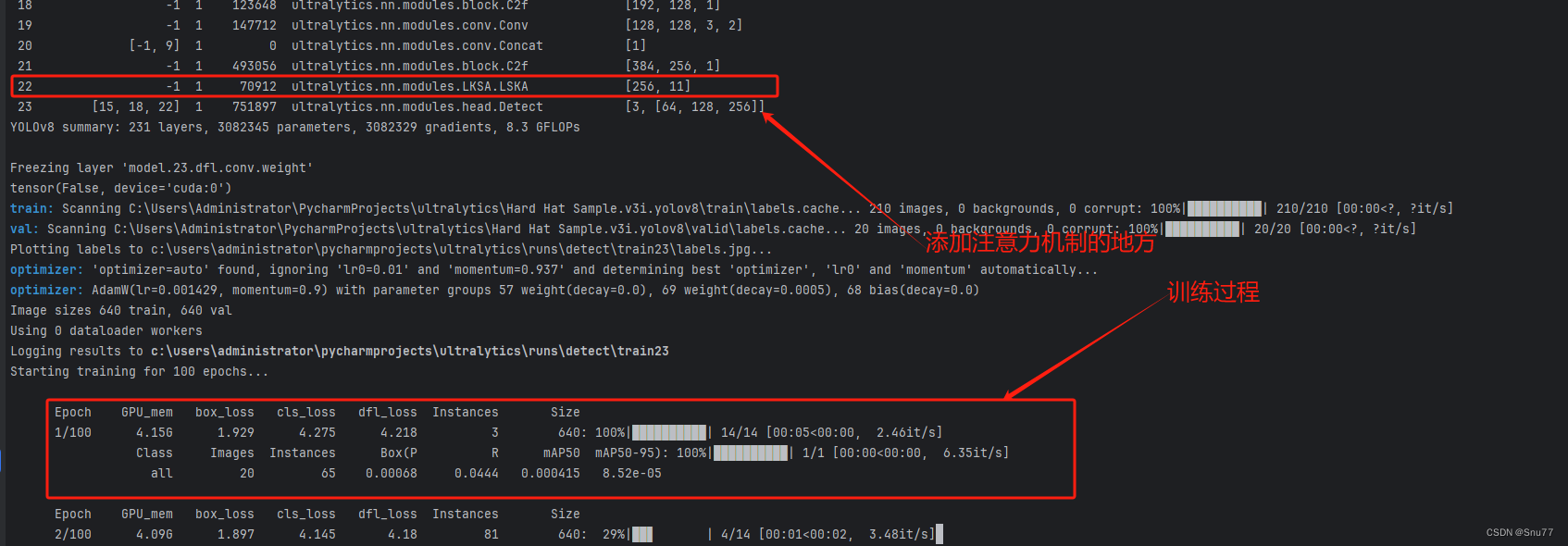
4.2.2 LSKAttention的訓練過程截圖?

下面是我添加了LSKAttention的訓練截圖。

?

五、LSKAttention可添加的位置

5.1 推薦LSKAttention可添加的位置?

LSKAttention可以是一種即插即用的注意力機制，其可以添加的位置有很多，添加的位置不同效果也不同，所以我下面推薦幾個添加的位，置大家可以進行參考，當然不一定要按照我推薦的地方添加。

  1. 殘差連接中：在殘差網絡的殘差連接中加入注意力機制(這個位置我推薦的原因是因為DCN放在殘差里面效果挺好的大家可以嘗試)

  2. 特征金字塔（SPPF）：在特征金字塔網絡之前，可以幫助模型更好地融合不同尺度的特征。

  3. Neck部分：YOLOv8的Neck部分負責特征融合，這里添加注意力機制可以幫助模型更有效地融合不同層次的特征。

  4. 輸出層前：在最終的輸出層前加入注意力機制可以使模型在做出最終預測之前，更加集中注意力于最關鍵的特征。

大家可能看我描述不太懂，大家可以看下面的網絡結構圖中我進行了標注。

5.2圖示LSKAttention可添加的位置?

?

六、本文總結?

到此本文的正式分享內容就結束了，在這里給大家推薦我的YOLOv8改進有效漲點專欄，本專欄目前為新開的平均質量分98分，后期我會根據各種最新的前沿頂會進行論文復現，也會對一些老的改進機制進行補充，目前本專欄免費閱讀(暫時，大家盡早關注不迷路~)，如果大家覺得本文幫助到你了，訂閱本專欄，關注后續更多的更新~

?專欄回顧：YOLOv8改進系列專欄——本專欄持續復習各種頂會內容——科研必備

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/167939.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/167939.shtml
英文地址，請注明出處：http://en.pswp.cn/news/167939.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

loginctl - 控制 systemd 登錄管理器

loginctl - 控制 systemd 登錄管理器

loginctl loginctl用途loginctl安裝開啟loginctl服務session操作user操作管理用戶服務 loginctl - Control the systemd login manager Redhat/centos平臺使用loginctl管理登錄用戶與session loginctl用途 控制 systemd 登錄管理器管理當前登錄的用戶和session loginctl安裝…
閱讀更多...
Peter算法小課堂—高精度加法

Peter算法小課堂—高精度加法

指針與數組 看看以下代碼&#xff0c;請預測答案 #include <bits/stdc.h> using namespace std; int x[10]{0,1,2,3,4,5,6,7,8,9}; int main(){cout<<x<<endl;cout<<x3<<endl;cout<<*x<<endl;cout<<*(x7)<<endl;cout&…
閱讀更多...
定制手機套餐---python序列

定制手機套餐---python序列

if __name__ __main__:print("定制手機套餐")print("")#定義電話時長&#xff1a;字典callTimeOptions{1:0分鐘,2:50分鐘,3:100分鐘,4:300分鐘,5:不限量}keyinput("請輸入電話時長的選擇編號&#xff1a;")valuecallTimeOptions.get(key)if val…
閱讀更多...
代碼隨想錄算法訓練營第五十四天|392.判斷子序列 115.不同的子序列

代碼隨想錄算法訓練營第五十四天|392.判斷子序列 115.不同的子序列

文檔講解&#xff1a;代碼隨想錄 視頻講解&#xff1a;代碼隨想錄B站賬號 狀態&#xff1a;看了視頻題解和文章解析后做出來了 392.判斷子序列 class Solution:def isSubsequence(self, s: str, t: str) -> bool:dp [[0] * (len(t)1) for _ in range(len(s)1)]for i in ra…
閱讀更多...
Java 關于批量插入遇到的問題 -sqlserver

Java 關于批量插入遇到的問題 -sqlserver

序言&#xff1a; 我們在做項目的時候&#xff0c;經常會遇到&#xff0c;對數據的新增動作&#xff0c;如果數據量很少的情況下&#xff0c;單個新增對性能還好&#xff0c;但是一旦涉及到 大數據量&#xff0c;如十萬&#xff0c;百萬&#xff0c;千萬&#xff0c;這個時候如…
閱讀更多...
RabbitMq使用與整合

RabbitMq使用與整合

MQ基本概念 MQ概述 MQ全稱 Message Queue&#xff08;[kju?]&#xff09;&#xff08;消息隊列&#xff09;&#xff0c;是在消息的傳輸過程中保存消息的容器。多用于分布式系統之間進行通信。 &#xff08;隊列是一種容器&#xff0c;用于存放數據的都是容器&#xff0c;存…
閱讀更多...
優秀的時間追蹤軟件Timemator for Mac輕松管理時間！

優秀的時間追蹤軟件Timemator for Mac輕松管理時間！

在現代社會&#xff0c;時間管理成為了我們工作和生活中的一大挑戰。如果你經常感到時間不夠用&#xff0c;無法高效地完成任務&#xff0c;那么Timemator for Mac將成為你的得力助手。 Timemator for Mac是一款出色的時間追蹤軟件&#xff0c;它可以幫助你精確記錄和管理你的…
閱讀更多...
Linux的基本指令 ( 一 )

Linux的基本指令 ( 一 )

目錄 前言 Linux基本指令 快速認識五個指令 ls指令 補充內容 pwd指令 補充內容 cd指令 補充內容 重新認識指令 指令的本質 which指令 alias指令 最后 一個文件的三種時間 tree指令及安裝 tree指令 前言 關于Linux操作系統的桌面&#xff0c;在學校教學中我們…
閱讀更多...
實用高效 無人機光伏巡檢系統助力電站可持續發展

實用高效 無人機光伏巡檢系統助力電站可持續發展

近年來&#xff0c;我國光伏發電行業規模日益壯大&#xff0c;全球領先地位愈發鞏固。為解決光伏電站運維中的難題&#xff0c;浙江某光伏電站與復亞智能達成戰略合作&#xff0c;共同推出全自動無人機光伏巡檢系統&#xff0c;旨在提高發電效率、降低運維成本&#xff0c;最大…
閱讀更多...
Spark---SparkCore（一）

Spark---SparkCore（一）

一、術語與寬窄依賴 1、術語解釋 1、Master(standalone):資源管理的主節點&#xff08;進程&#xff09; 2、Cluster Manager:在集群上獲取資源的外部服務(例如&#xff1a;standalone,Mesos,Yarn) 3、Worker Node(standalone):資源管理的從節點(進程)或者說管理本機資源的…
閱讀更多...
用Python寫一個瀏覽器集群框架

用Python寫一個瀏覽器集群框架

更多Python學習內容&#xff1a;ipengtao.com 在分布式爬蟲和大規模數據采集的場景中&#xff0c;使用瀏覽器集群是一種有效的方式&#xff0c;可以提高數據采集的速度和效率。本文將介紹如何用Python編寫一個簡單但強大的瀏覽器集群框架&#xff0c;以應對需要使用多個瀏覽器實…
閱讀更多...
WebGL/threeJS面試題掃描與總結

WebGL/threeJS面試題掃描與總結

什么是 WebGL&#xff1f;什么是 Three.js&#xff1f;請解釋three.js中的WebGL和Canvas的區別&#xff1f; WebGL(全寫Web Graphics Library)是一種3D繪圖協議&#xff0c;這種繪圖技術標準允許把JavaScript和OpenGL ES 2.0結合在一起&#xff0c;通過增加OpenGL ES 2.0的一個…
閱讀更多...
分庫分表、分布式數據庫、MPP

分庫分表、分布式數據庫、MPP

分庫分表、分布式數據庫、MPP的區別嗎&#xff1f; 一、MySQL分庫分表和MySQL分布式集群在性能方面各有優劣&#xff0c;具體取決于應用場景和需求。 MySQL分庫分表&#xff1a; 在分庫分表的場景下&#xff0c;可以將負載分散到多個數據庫實例上&#xff0c;從而提高整體性能…
閱讀更多...
【模糊測試】課堂筆記

【模糊測試】課堂筆記

模糊測試 模糊測試過程通常是自動化的。這個過程經典地分為以下幾個階段。 準備&#xff1a;這是第一階段&#xff0c;重點是 SUT 輸入和輸出格式的識別和規范。基于此&#xff0c;規范可以減少生成初始無效模糊數據的可能性并創建有效且精確的輸入。Fuzz Data Generation&am…
閱讀更多...
思科模擬器操作命令

思科模擬器操作命令

模式 思科模擬器常見的模式有 用戶模式 能夠操作的命令比較少 特權模式特權模式下面可以操作的比較多 全局模式 接口模式 用戶模式進入特權模式: 命令enable 特權模式進行全局模式命令: configure terminal 退出命令 exit命令&#xff1a;返回上一層&#xff0c;即一步一步…
閱讀更多...
RocketMQ 消息中間件 知識點匯總

RocketMQ 消息中間件 知識點匯總

目錄 RocketMQ1、什么是RocketMQ？常用術語：2、為什么需要消息隊列3、什么是異步處理4、什么是服務解耦5、什么是流量控制6、消息隊列兩種模型隊列模型：發布/訂閱模型：總結：7、怎么保證消息不丟失8、如何處理消息被重復消費**出現消息重復的情況：****解決方法：**9、如何保…
閱讀更多...
流量分析-PhishingEmail_WriteUp

流量分析-PhishingEmail_WriteUp

一、題目問題 問題1&#xff1a;黑客的email名稱 問題2&#xff1a;黑客向幾人發送了釣魚郵件 問題3&#xff1a;黑客傳輸的木馬文件名 問題4&#xff1a;下載并運行了木馬文件的人的email名稱和ip地址&#xff0c;用“-”連接 問題5&#xff1a;黑客用于反彈shell的主機i…
閱讀更多...
什么葡萄酒會適用這種雙重潷析方法呢？

什么葡萄酒會適用這種雙重潷析方法呢？

潷析有兩個主要目的&#xff0c;一種是去除陳年或未經過濾的葡萄酒中的沉淀物。雖然沉淀物不會對你造成任何傷害&#xff0c;但當喝葡萄酒滿嘴都是葡萄沉淀物時是一件很糟糕的事。其次&#xff0c;傾析葡萄酒是可以讓葡萄酒“呼吸”與氧氣接觸的&#xff0c;氧氣可以軟化單寧&a…
閱讀更多...
二維數值型數組例題

二維數值型數組例題

1、單位矩陣初始化 題目描述 對用作單位矩陣的數組初始化。單位矩陣在主對角線上的值為1&#xff0c;而其他的地方的值為0&#xff0c;并且主對角線上的行、列下標是一樣的。 輸入要求 輸入一個整數n表示矩陣的行數 輸出要求 輸出n*n的單位矩陣。數據之間以空格間隔&…
閱讀更多...
LeetCode Hot100 102.二叉樹的層序遍歷

LeetCode Hot100 102.二叉樹的層序遍歷

題目&#xff1a; 給你二叉樹的根節點 root &#xff0c;返回其節點值的 層序遍歷 。 &#xff08;即逐層地&#xff0c;從左到右訪問所有節點&#xff09;。 方法&#xff1a;迭代 class Solution {public List<List<Integer>> levelOrder(TreeNode root) {if …
閱讀更多...
最新文章

Copyright @ 2022~2023