1.冒泡排序

1.1基礎冒泡排序

算法思想

冒泡排序是最簡單的排序算法了。冒泡排序通過不斷地比較兩個相鄰元素，將較大的元素交換到右邊（升序），從而實現排序。那我們直接看例子。

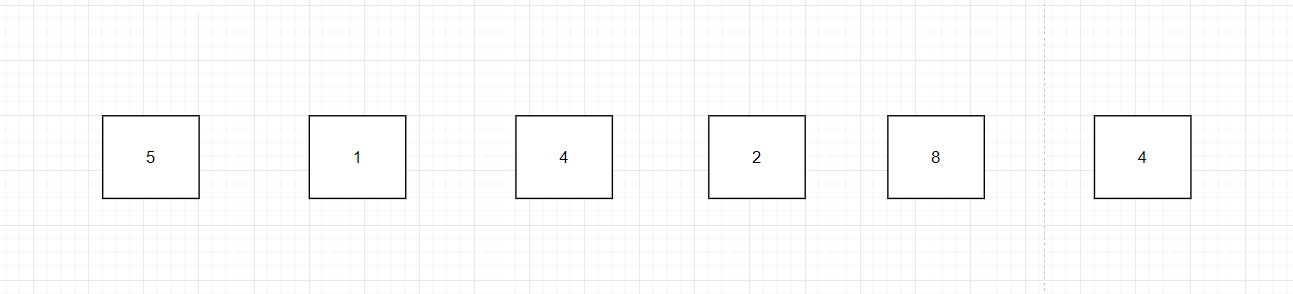
我們對數組 [5，1，4，2，8，4] ，采用冒泡排序進行排序，注意這里的兩個 4 的顏色是不同
的，主要是為了區分兩個不同的 4 ，進而解釋冒泡排序算法的穩定性問題。

第一輪冒泡排序：第一步：比較 5 和 1 ，5 > 1，則交換 5 和 1 的位置：

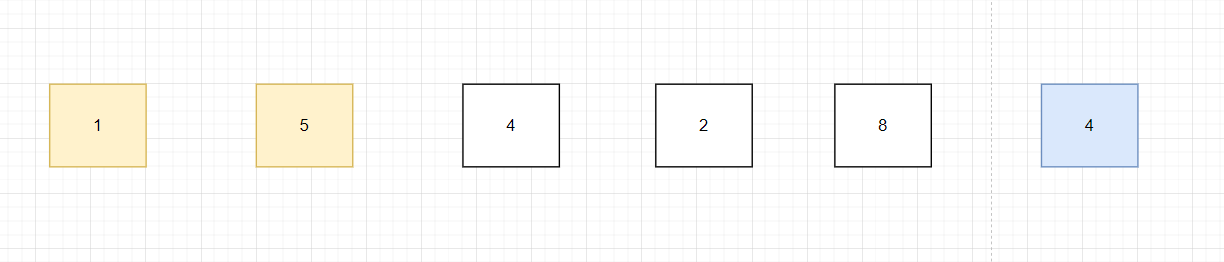
第二步，比較 5 和 4，5 > 4，交換 5 和 4 的位置：

第三步：比較 5 和 2 ，5 > 2，交換 5 和 2 的位置：

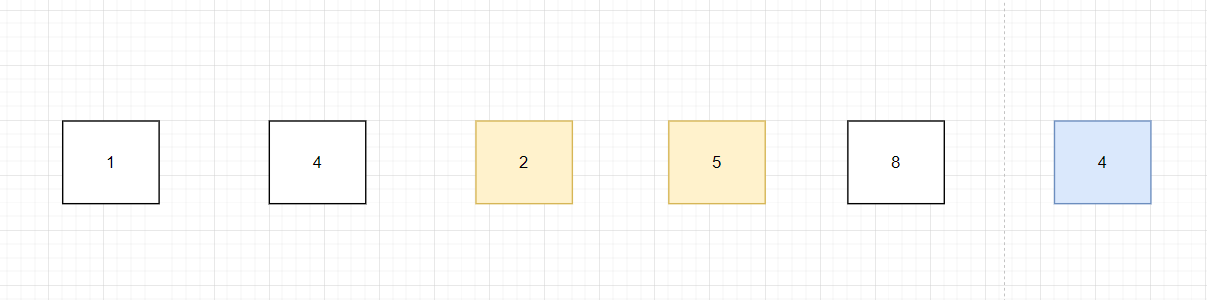
第四步：比較 5 和 8 ，5 < 8 ，不交換

第五步：比較 8 和 4 ， 8 > 4，交換 8 和 4 ：

此刻我們獲得數組當中最大的元素 8 ，使用橘?色進行標記：

第一輪冒泡結束，最大的元素8到了最后，然后對于前面5個元素，進行第二輪冒泡將第二大的數據放在右邊。

最終結果：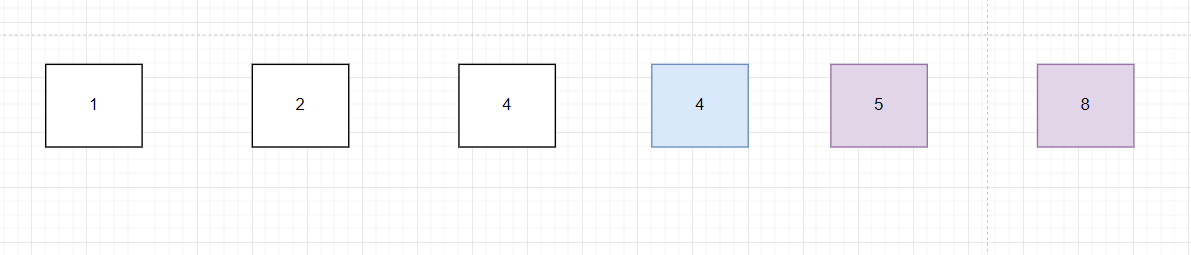
事實上第二階段結束，整個數組已經有序了，但是對于冒泡排序而言并不知道，她還需要通過第三階段的比較操作進行判斷。

對于冒泡排序算法而言，她是通過判斷整個第三階段的比較過程中是否發生了交換來確定數組是否有序的，顯然上面的過程中沒有交換操作，冒泡排序也就知道了數組有序，整個算法執行結束。

1.1.1基礎冒泡排序代碼實現

void bubbleSortV1(SortTable *table) {for (int i = 0; i < table->length-1; ++i) {for (int j = 0; j < table->length-1-i; ++j) {if (table->data[j].key > table->data[j+1].key) {swapElement(&table->data[j+1],&table->data[j]);}}}
}

這里面的swapElement是我測試框架里的代碼，作用是交換兩個元素的位置，外層循環用于把最大的元素冒到右邊去，內層循環從0開始length-1-i，才能完整掃描未排好區間，實現“冒泡”效果。注意第二層循環的上界，最右邊 i 個元素已經是有序區，不需要再碰，所以上界寫成 table->length-1-i。

來測一下：

#include"bubbleSort.h"
void test01() {int n=100000;SortTable *table1=generateRandomArray(n,0,1+5000);testSort("bubbleSortV1",bubbleSortV1,table1);releaseSortTable(table1);
}int main() {test01();return 0;
}

結果:

D:\work\DataStruct\cmake-build-debug\04_Sort\SwapSort.exe
bubbleSortV1 cost time: 20.063000s.進程已結束，退出代碼為 0

可以看到同樣是十萬個元素上一節課中的插入排序幾秒鐘就能完成，但是這里的冒泡排序需要20幾秒，原因在于無論數據是否已經有序，都要跑完全部 n-1 趟且交換次數往往也很高，我們就在想能不能優化一下呢？

1.2冒泡排序的一次優化

這里我們增加了一個標識數組是否有序 ，當冒泡排序過程中沒有交換操作時，swapped = false ，也意味著數組有序；否則數組無序繼續進行冒泡排序。不要小看這個變量奧，因為這個變量，當數組有序的時候，冒泡排序的時間復雜度將降至 O(n)(因為其只需要執行一遍內層的 for 循環就可以結束冒泡排序)，沒有這個變量，數組有序也需要O(n²)的時間復雜度。講直白點因為冒泡排序始終把大的元素冒到右邊，可以當作右邊始終是有序的，當發現某一輪不需要交換，那么就說明已經有序，退出循環。

1.2.1冒泡排序的第一次優化代碼實現

void bubbleSortV2(SortTable* table) {for (int i = 0; i < table->length - 1; ++i) {int isSorted = 1;for (int j = 0; j < table->length - 1 - i; ++j) {if (table->data[j].key > table->data[j + 1].key) {swapElement(&table->data[j + 1], &table->data[j]);isSorted = 0;}}if (isSorted) {break;}}
}

來測一下：

#include"bubbleSort.h"
void test01() {int n=10000;SortTable *table1=generateRandomArray(n,0,1+5000);SortTable *table2=copySortTable(table1);testSort("bubbleSortV1",bubbleSortV1,table1);testSort("bubbleSortV2",bubbleSortV2,table2);releaseSortTable(table1);releaseSortTable(table2);
}int main() {test01();return 0;
}

結果:

D:\work\DataStruct\cmake-build-debug\04_Sort\SwapSort.exe
bubbleSortV1 cost time: 0.130000s.
bubbleSortV2 cost time: 0.130000s.進程已結束，退出代碼為 0

這里看不出來精度差是因為我們產生的數據太隨機了，意義不太大，但是這種思想要學會。

1.3冒泡排序的二次優化

一次優化是為了避免數組有序的情況下，繼續進行判斷操作的。那么二次優化又為了什么呢 ？

我們看下面的例子。

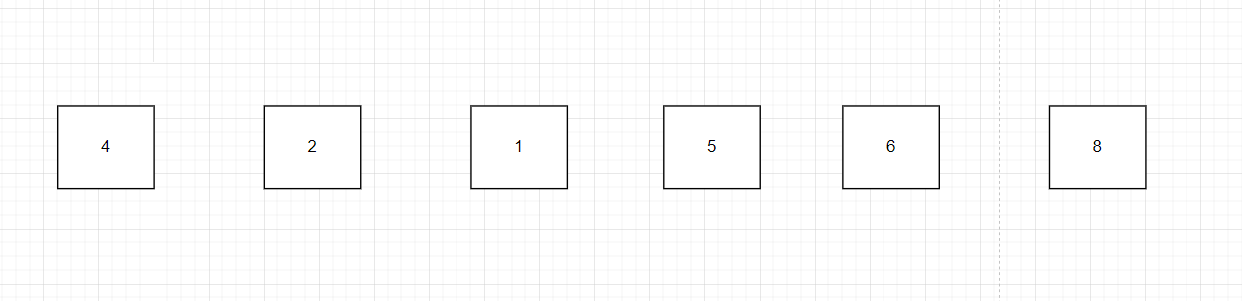
經過一次冒泡后，我們會注意到一個問題，但是我們注意到，數組數組中的 [5,6,8] 本身已經有序，而對于有序的部分進行比較是沒有意義的，相當于在白白浪費資源，有沒有什么辦法減少這樣的比較次數呢？

換句話說，是否能夠確定出已經有序部分和無序部分的邊界呢？

答案當然是肯定的，這個邊界就是第一趟冒泡排序的過程中最后一次發生交換的位置 j ：也就是 1 和 4 發生交換之后，4 和 5 沒有發生交換，此時 1 之后的元素為有序。

第一步：4 和 2比較，4 > 2 ，交換 4 和 2 ，將 LastSwappedIndex = 0；

第二步：4 和 1 比較，4 > 1，交換 4 和 1， LastSwappedIndex = 1 ；

第三步：比較 4 和 5 ， 4 < 5，不交換， lastSwappedIndex 也不更新;

第四步：比較 5 和 6 ，不交換， lastSwappedIndex 也不更新;

第五步：比較 6 和 8 ，不交換， lastSwappedIndex 也不更新;

第一趟冒泡排序結束了，我們把 LastSwappedIndex放在了4這里，相當于是一個擋板

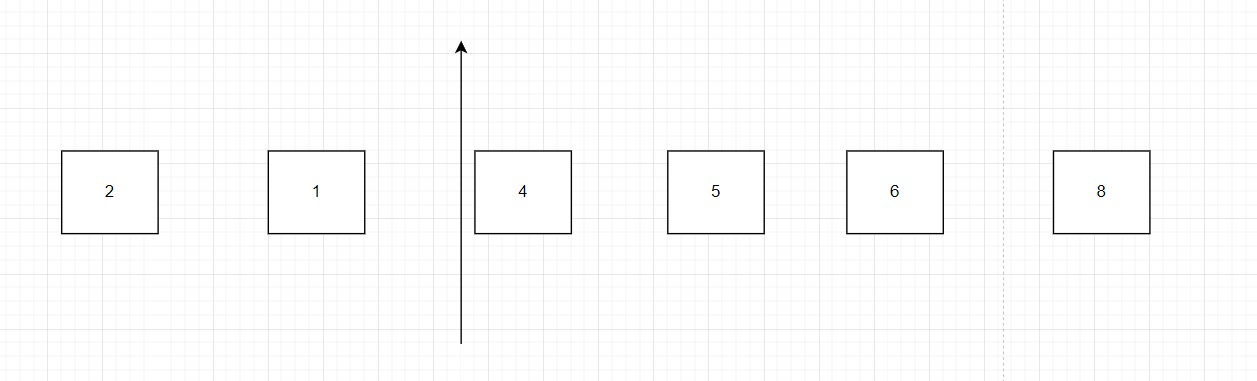
來看第二趟冒泡排序，此時 j 的 取值將從 j = 0 到 j = lastSwappedIndex ，第一步：比較 2 和 1 ，2 > 1，交換，lastSwappedIndex = 0 ，并且第二趟冒泡也就結束了，也就說我們節省了 從 2 到 6的比較操作；

最后再來一趟冒泡排序，發現沒有任何交換，所以冒泡排序結束。

相比于一次優化的實現方式，二次優化的實現方式進一步減少了不必要的執行次數，兩種優化后的實現方式需要冒泡排序的趟數是一樣的，本質上沒有什么區別。所以即使對于一個有序的數組，兩種方式的時間復雜度都是O（n）

1.3.1 冒泡排序的二次優化代碼實現

/* 引入newIndex標記交換的索引位置，下次冒泡的時候結束位置就是newIndex */
void bubbleSortV3(SortTable* table) {int newIndex;int n = table->length;do {newIndex = 0;for (int i = 0; i < n - 1; ++i) {if (table->data[i].key > table->data[i + 1].key) {swapElement(&table->data[i + 1], &table->data[i]);newIndex = i + 1;}}//更新擋板位置n = newIndex;} while (newIndex > 0);
}

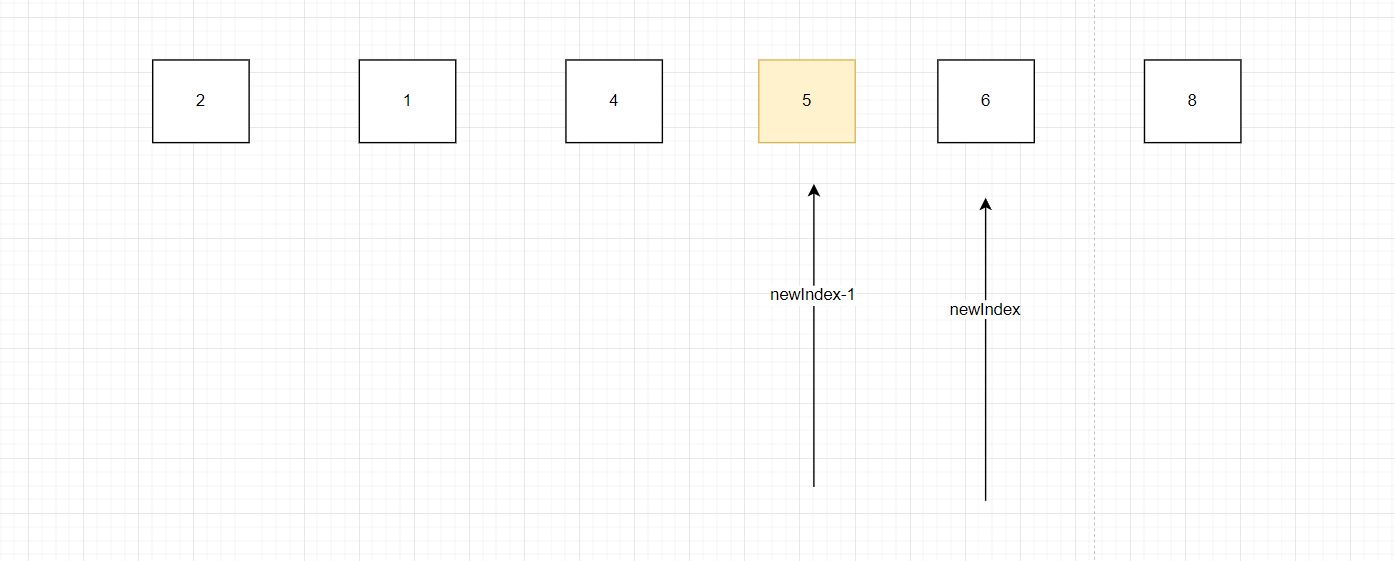
注意要把i+1賦給newIndex，如果賦的是i由于我們for循環中循環條件是n-1就會少一個數的排序，如圖假設newIndex在6，本來該是2，1，4，5冒泡排序，但是由于newIndex-1賦值給n，n-1為循環條件就會導致5沒有參與冒泡排序。

來測一下：

#include"bubbleSort.h"
void test01() {int n=10000;SortTable *table1=generateRandomArray(n,0,1+5000);SortTable *table2=copySortTable(table1);SortTable *table3=copySortTable(table1);testSort("bubbleSortV1",bubbleSortV1,table1);testSort("bubbleSortV2",bubbleSortV2,table2);testSort("bubbleSortV3",bubbleSortV3,table3);releaseSortTable(table1);releaseSortTable(table2);
}int main() {test01();return 0;
}

結果：

D:\work\DataStruct\cmake-build-debug\04_Sort\SwapSort.exe
bubbleSortV1 cost time: 0.129000s.
bubbleSortV2 cost time: 0.131000s.
bubbleSortV3 cost time: 0.125000s.進程已結束，退出代碼為 0

看的出來第二次優化會比前兩次是要好一點的

2.快速排序

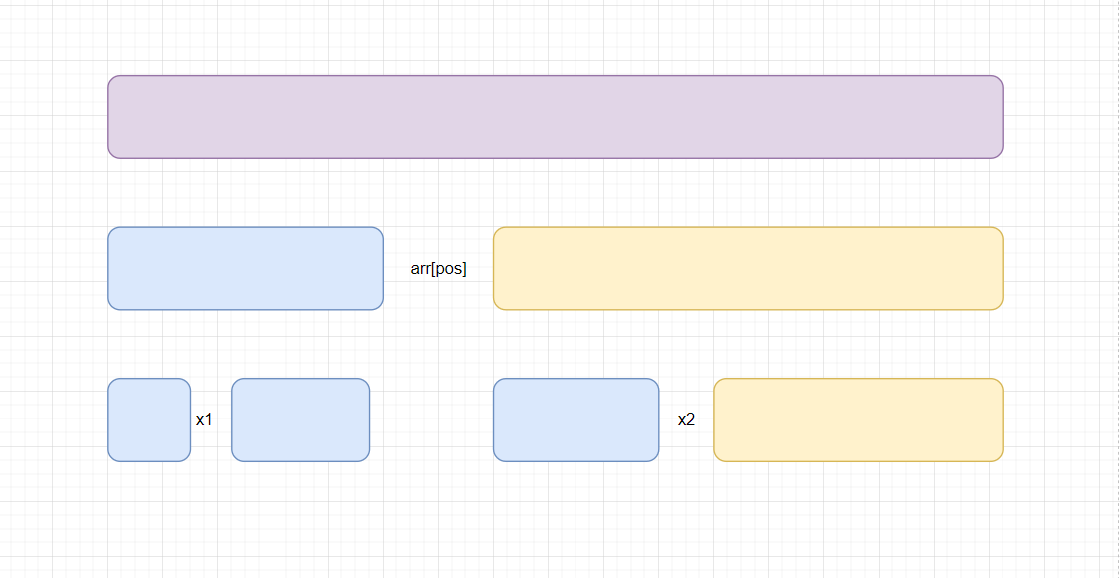
找pos犄點，pos是索引號，pos對應的值的左邊都是比pos值小的，pos對應的值的右邊都是比pos值大的，這樣咱們就把要排序的序列分成兩部分，我們拿排序的最差時間復雜度來說，假設左邊部分有x個元素，右邊部分為y個，那么分別排序這兩個序列的時間復雜度為x²+y²而沒有拆分前的時間復雜度是x²+y²+2xy,同理在左邊部分的序列又可以找一個犄點，右邊部分的序列也可以找一個犄點。如圖所示：
如果我們每次的犄點都是均分，一直分下去最后的時間復雜度為nlogn。找犄點的方法有兩種：雙邊循環法，單邊循環法。

2.1雙邊循環法

所謂雙邊就是兩個指針在左右，用這兩個指針從數組兩端向中間“夾擊”，隨機初始化一個犄點把小于犄點的元素換到左邊、大于犄點的元素換到右邊，直到兩指針相遇。初始時的犄點是隨機取得，這里我就把它放在數組得最左邊，如圖：

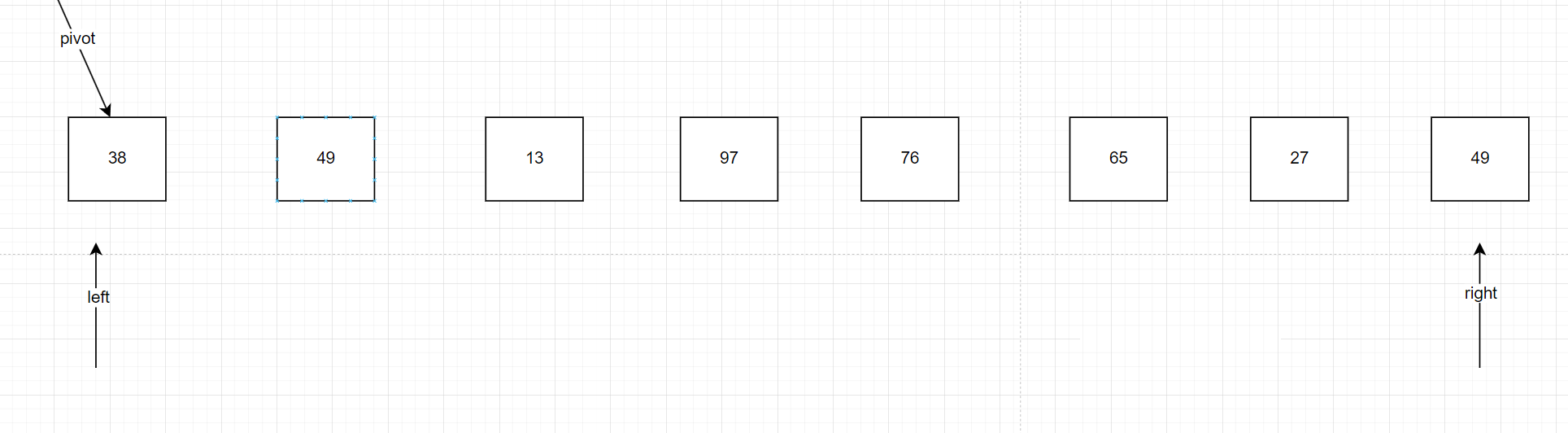
來看右邊right，看右邊的指針是否比初始時犄點值大，發現是49沒問題，right往左邊走一步來到27，發現27比38小，說明應該在犄點的左邊；left最初指向38，可以認為大于等于初始時犄點的值，left往右走一步來到49，49比38大，說明應該在犄點的右邊，我們應該把兩個值交換位置，注意一定要先操作右邊，找到第一個比我們最初設定的犄點值小的數，如果暫時沒有，就先一直操作右邊right–，保證右邊先找到，再去操作左邊，找到第一個比我們最初設定的犄點值大的數，如果暫時沒有，就再一直操作右移,兩者都找到了就交換位置如圖

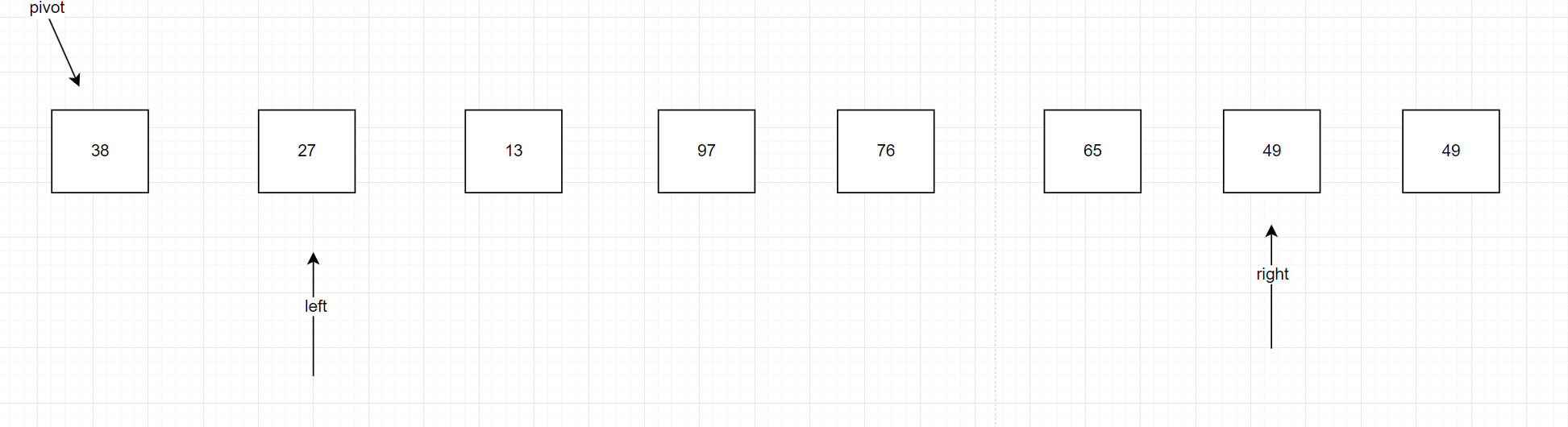
right往右一直走到13發現比38小了，left往左邊走，相碰了，我們找到了犄點所在位置，我們就交換38和13的位置。如圖，犄點左邊的值確實比犄點的值小，犄點右邊的值確實比犄點的值大，同理在新分出來的左，右邊依然可以采取這種方法直到left和right相碰，很明顯這是一種遞歸的是方法，下面我們來看怎么實現代碼

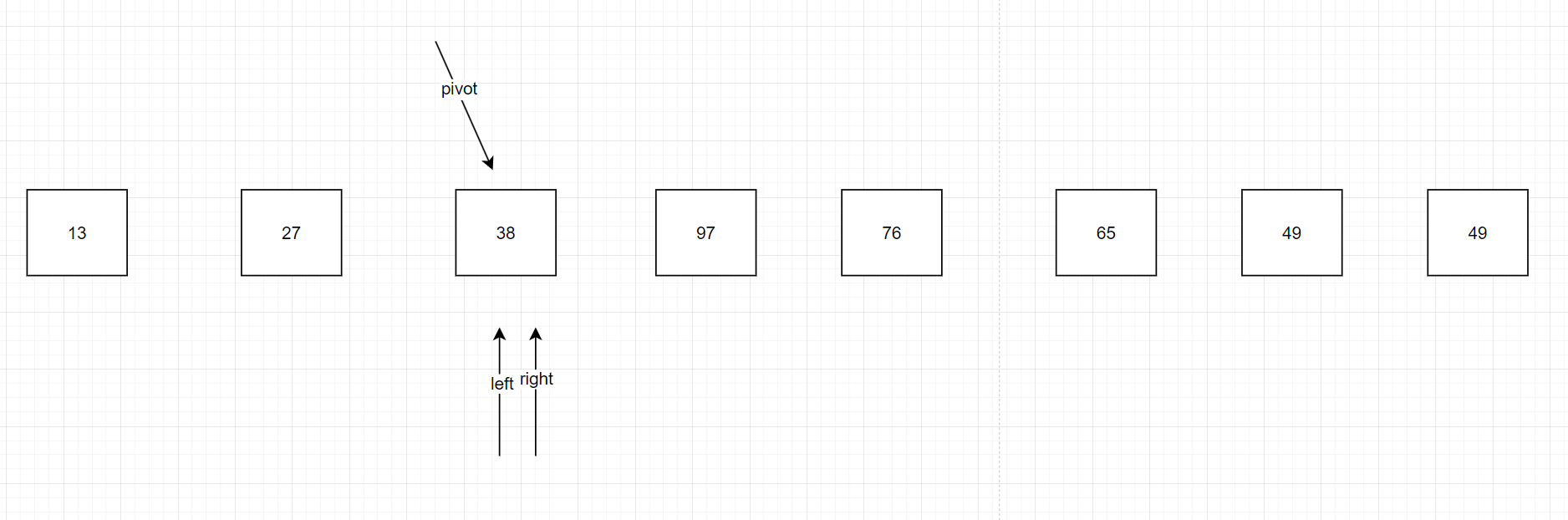
2.1.1雙邊循環法的代碼實現

static int partitionDouble(SortTable *table, int startIndex, int endIndex) {int pivot = startIndex;int left = startIndex;int right = endIndex;// 隨機將startIndex和后續的一個隨機索引指向的元素進行交換while (left != right) {while (left < right && table->data[right].key > table->data[pivot].key) { right--; }while (left < right && table->data[left].key <= table->data[pivot].key) { left++; }if (left < right) {swapElement(&table->data[right], &table->data[left]);}}swapElement(&table->data[pivot], &table->data[left]);return left;
}// 用遞歸思想實現[start, end]區間的排序
static void quickSort1(SortTable *table, int startIndex, int endIndex) {if (startIndex >= endIndex) {return;}// 找到犄點int pivot = partitionDouble(table, startIndex, endIndex);quickSort1(table, startIndex, pivot - 1);quickSort1(table, pivot + 1, endIndex);
}void quickSortV1(SortTable* table) {quickSort1(table, 0, table->length - 1);
}

我們先來看大框架：static void quickSort1(SortTable *table, int startIndex, int endIndex);我們需要通過找犄點把整個序列按左邊小右邊大的思路一直分下去，所以我們需要寫一個找犄點的函數，找到后開始遞歸，把新的左右兩邊的序列再次通過犄點分成左右兩份，但是我們不能無限遞歸下去，所以我們需要寫一個遞歸終止條件，只要子區間長度 ≤ 1，即 startIndex >= endIndex，就已經有序，無需再排，然后我們在
void quickSortV1(SortTable *table)調用這個函數，并賦值starIndex和endIndex。

接下來看找犄點的代碼，我們把最初的基準pivot放到startIndex上，當左邊left小于等于右邊right的時候，開始先對右邊處理邏輯，再對左邊處理邏輯。有人可能會問，為什么外層循環已經有left<=right，內層循環為什么還要加呢？當出現如下圖所示情況時如果在內層while循環中沒有left<right的話，right就會一直減。同理處理左邊的時候也需要加上left<right這個條件。外層循環只是控制分區過程是否繼續，內層循環防止單指針移動時越界/交叉，確保每次移動后仍滿足指針有效性。前面這兩是必須的，if中的left<right避免指針重合時的無效交換，推薦使用

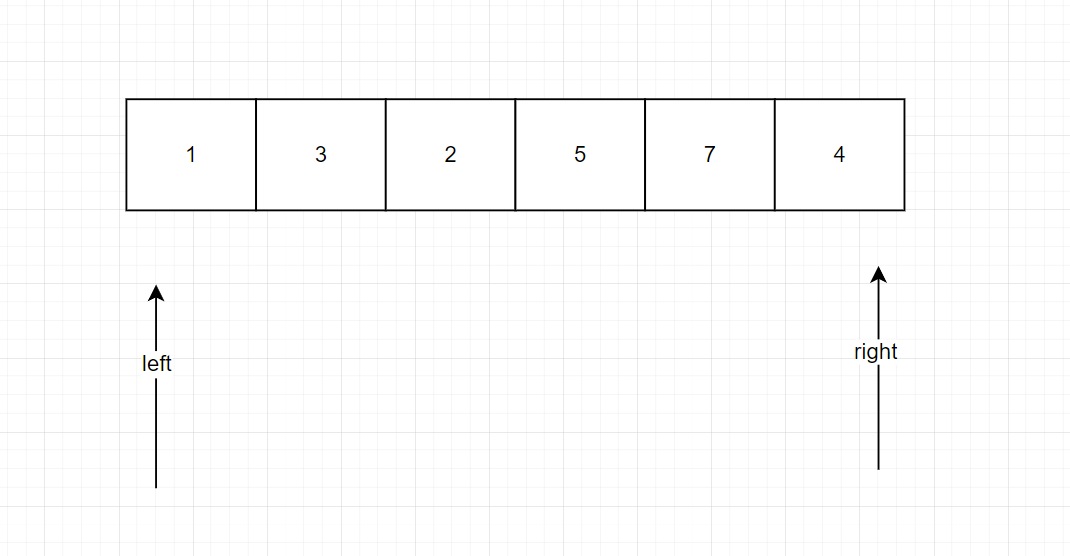
來測試一下：

#include"bubbleSort.h"
#include"quickSort.h"
void test02() {int n = 10000;SortTable *table1 = generateRandomArray(n, 0, n + 5000);SortTable *table2 = copySortTable(table1);testSort("bubbleSortV3", bubbleSortV3, table1);testSort("quick SortV1", quickSortV1, table2);releaseSortTable(table1);}int main() {test02();return 0;
}

結果：

D:\work\DataStruct\cmake-build-debug\04_Sort\SwapSort.exe
bubbleSortV3 cost time: 0.131000s.
quick SortV1 cost time: 0.000000s.進程已結束，退出代碼為 0

能夠看出快速排序的時間比冒泡排序的時間快的多，接下來看單邊循環法

2.2單邊循環法

我們依舊需要一個犄點，犄點的左值小于犄點，犄點的右值大于犄點，只不過我們用一個指針來處理結構，我們把這個犄點重新起個名字叫mark，幫忙維護整個序列的指針我們先稱為i，依舊先把序列的最左邊當作我們的犄點。如下圖初始時

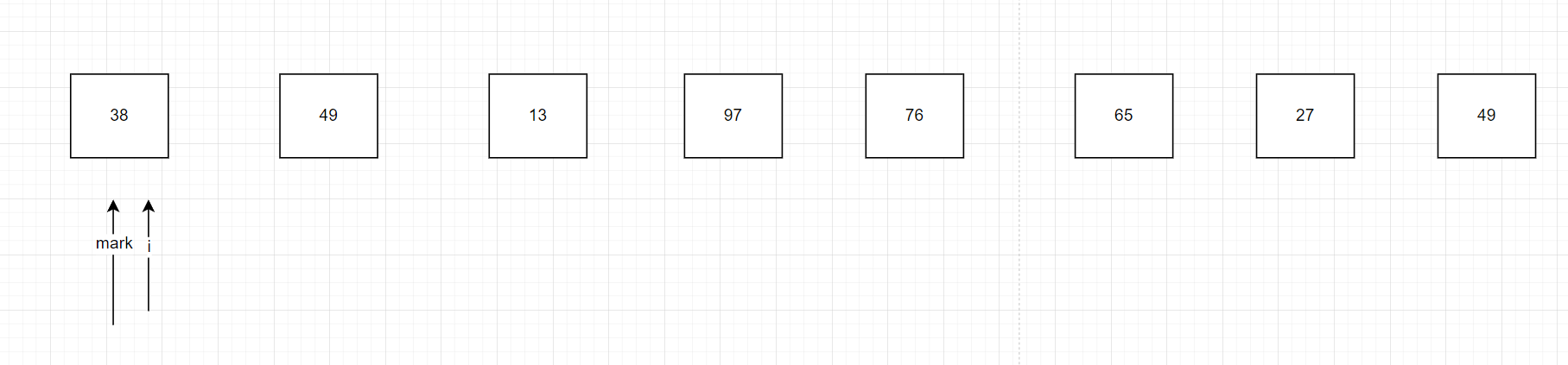
我們的i不斷地往右邊走，當走到i對應的值大于基礎值38的時候我們就不管，當發現我們的i對應的值小于了38時，我們mark往右邊走一位，然后交換mark指向的值和i指向的值，為什么mark要先往右邊走一位呢，因為最終我們38會和我們最終確定的mark交換位置，我們需要保證最后交換后的mark的左邊全部小于mark對應的值。反過來說，我們找到了對應i的值小于了基礎值38后，mark要往后面走一位給我們找到的數據空一格位置出來，我們走到13的時候發現13比38小，mark往右邊移動一位，和i指向的值交換

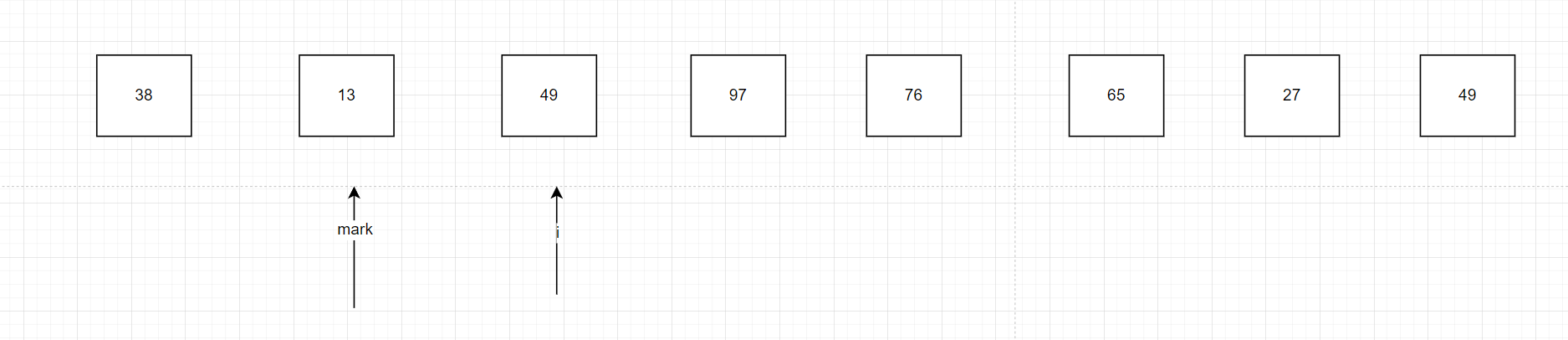
下一次找到比38小的數是27，我們依舊采用這樣的思路如圖所示：

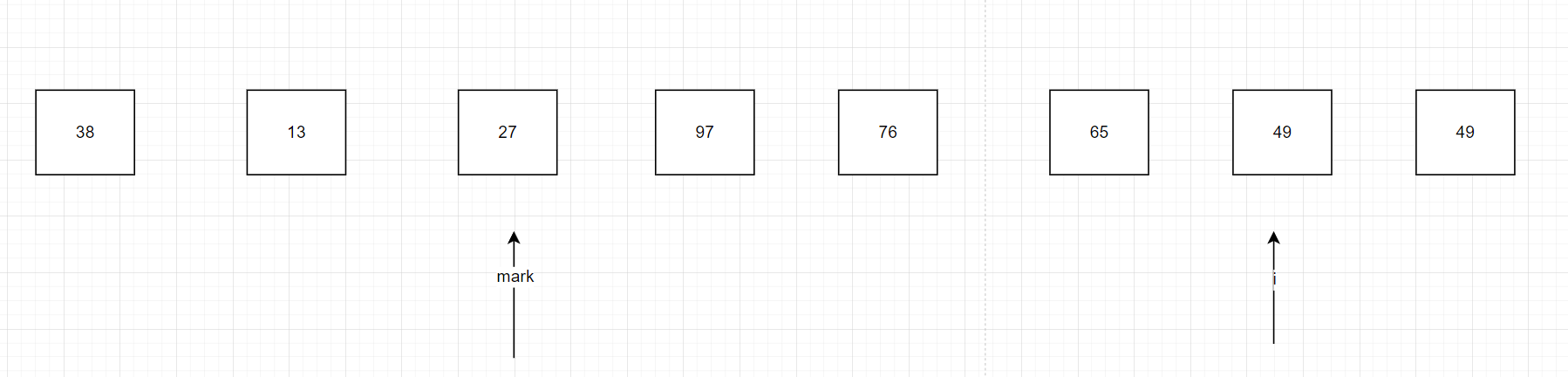
i繼續往后面走，發現mark的右邊已經全部比38大了，這時我們交換38和mark指向的27的位置即可。

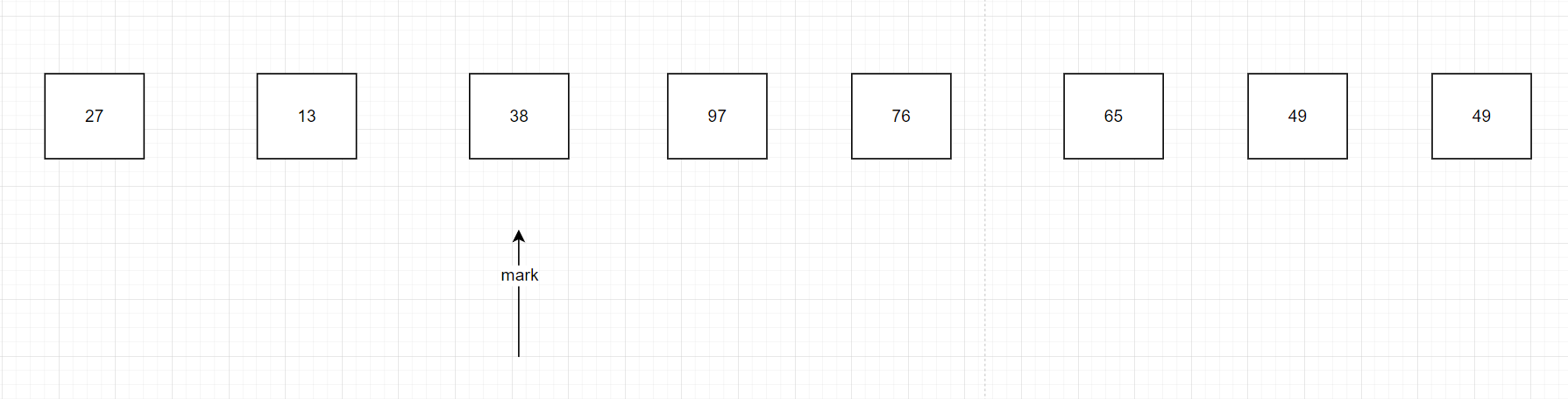
2.2.1單邊循環法代碼實現

static int partitionSingle(SortTable *table, int startIndex, int endIndex) {keyType tmpValue = table->data[startIndex].key;//備份一下第一個基準值int mark = startIndex;//假設第一個是犄點for (int i = startIndex + 1; i <= endIndex; i++) {if (table->data[i].key < tmpValue) {mark++;swapElement(&table->data[i], &table->data[mark]);}}swapElement(&table->data[startIndex], &table->data[mark]);return mark;
}static void quickSort2(SortTable *table, int startIndex, int endIndex) {if (startIndex >= endIndex) {return;}// 找到犄點int pivot = partitionSingle(table, startIndex, endIndex);quickSort2(table, startIndex, pivot - 1);quickSort2(table, pivot + 1, endIndex);
}void quickSortV2(SortTable* table) {quickSort2(table, 0, table->length - 1);
}

這里的邏輯就是我上述說的邏輯。

#include"bubbleSort.h"
#include"quickSort.h"void test02() {int n = 10000;SortTable *table1 = generateRandomArray(n, 0, n + 5000);SortTable *table2 = copySortTable(table1);SortTable *table3 = copySortTable(table1);testSort("bubbleSortV3", bubbleSortV3, table1);testSort("quick SortV1", quickSortV1, table2);testSort("quick SortV2", quickSortV2, table3);releaseSortTable(table1);releaseSortTable(table2);releaseSortTable(table3);
}int main() {test02();return 0;
}

結果：

D:\work\DataStruct\cmake-build-debug\04_Sort\SwapSort.exe
bubbleSortV3 cost time: 0.123000s.
quick SortV1 cost time: 0.001000s.
quick SortV2 cost time: 0.001000s.進程已結束，退出代碼為 0

大概先寫這些吧，今天的博客就先寫到這，謝謝您的觀看。