背景

BEV感知能夠聚合多個傳感器輸入得到統一的空間表征，在3D感知、下游應用以及跨模態融合中發揮重要作用。現有的BEV感知分為2D反投影（LSS）以及3D投影（BEVFormer），其中3D投影依賴于3D體素的投影，這導致BEV網格分辨率不能太大，否則計算代價高。本文提出了基于2D反向投影方法，在準確度與計算效率間取得平衡并滿足實時性要求。

相關工作

投影方法

對于3D投影來說，相比于2D反投影它是計算密集型的，對網格分辨率有較高要求，限制了在現實場景下的可擴展性。
對于2D反投影來說，LSS提出將2D特征抬升到3D空間中，但他依賴于準確的深度估計，深度估計錯會傳播到BEV表征中，因此后續的BEVStereo、BEVDepth都引入了深度損失作為輔助損失。雖然它們使用了概率深度估計來soft的抬升特征，但是還是缺乏顯式的深度不確定性的表示，在復雜場景下很難處理深度模糊性的問題。GaussianLSS通過計算概率深度分布的方差來建模深度不確定性，從而降低了對于準確深度的依賴轉為捕獲圍繞均值深度的空間范圍。

不確定性建模

不確定性建模就是在建模或預測時不是給出一個準確的值，而是給出預測結果+結果的信心程度。評估不確定性的方法包含以下幾種：

• 預測分布的方差。計算概率分布的方差，從而在輸出中提供直接反映信心程度的信息。
• 基于MLP的不確定評估。它是通過多層的MLP網絡得到一個不確定性分數，又或者是輸出一個分布的參數u與σ，其中σ作為方差衡量不確定性。
• 貝葉斯網絡。使用分布的先驗建模不確定性。
  在這篇論文中，則是通過分布的方差來建模不確定性從而提升BEV表征，尤其是在深度模糊的情況下。

主要工作

深度不確定性建模

LSS的主要問題：1、離散深度導致稀疏BEV，空間覆蓋率低。2、不穩定的深度分布，softmax得到的深度概率即使兩個bin靠近也可能大不相同，從而導致BEV特征不一致，這是由于softmax會是大的更大，小的更小，深度值輕微的不同可能導致不成比例的深度關注度。
本文是在預測的深度分布的基礎上計算它的均值與方差，使用錯誤容忍因子得到[u-kσ，u+kσ]的范圍，這個范圍考慮了深度不確定性，實現更靈活可靠的深度投影。

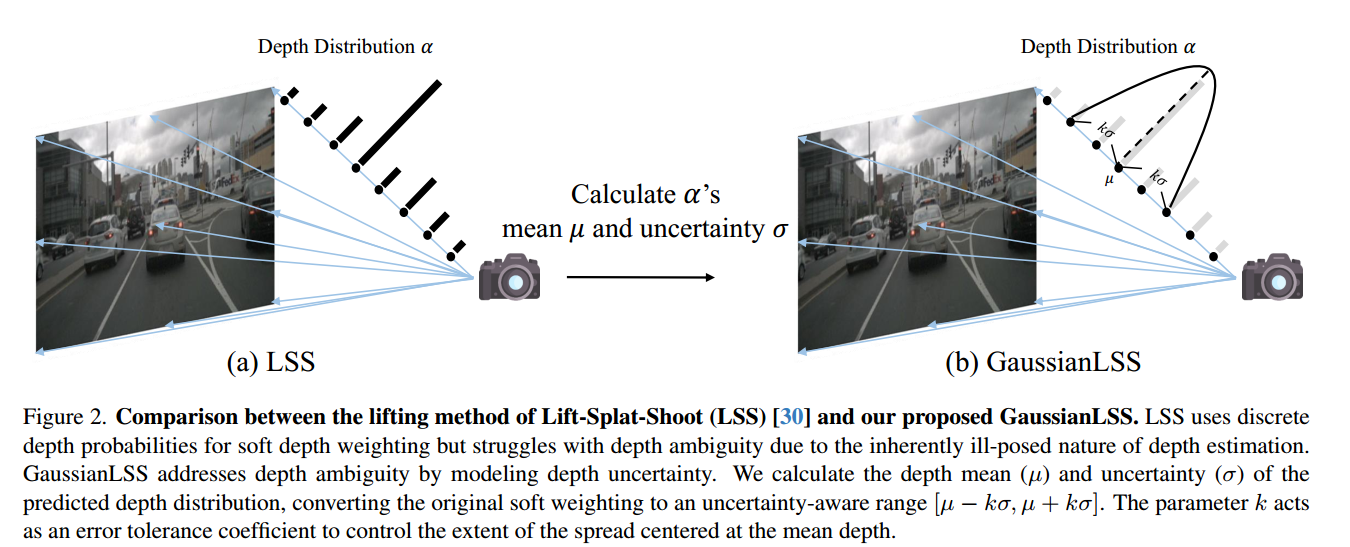
3D不確定性變換

對得到的深度范圍點，通過內外參轉換到自車坐標系下，計算出每個像素對應的均值與協方差，公式如下：
$${\mu }_{3d}=\sum _{i=0}^{B?1}{P}_i(p)p_i^{3d}$$
$$\Sigma =\sum _{i=0}^{B?1}{P}_i(p)(p_i^{3d}?{\mu }_{3d})(p_i^{3d}?{\mu }_{3d}{)}^T$$
使用馬氏距離定義置信范圍，利用了上面使用過的錯誤容忍系數，公式如下：
$$(x?{\mu }_{3d}{)}^T{\Sigma }^{?1}(x?{\mu }_{3d})\le k^2$$

BEV Features Splatting

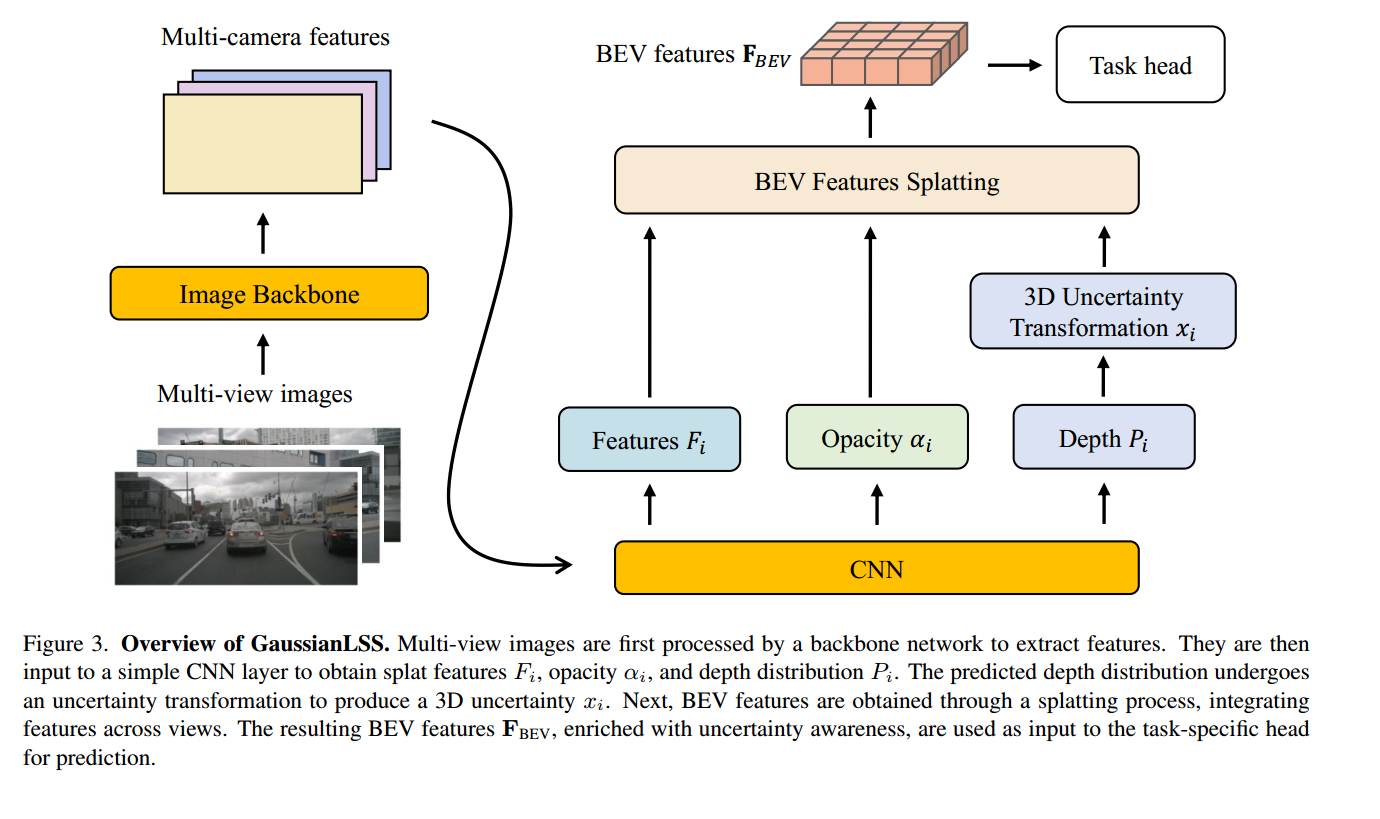
對于提取的特征分別輸出context，opacity與depth，其中depth通過3D不確定性變換得到兩個參數作為后續的輸入，利用Gaussian Splatting投射到BEV視角。
$$F_{BEV}(x)=\sum _{i\in G_{BEV}}{F}_i{\alpha }_i\exp \left(?\frac{1}{2}(x?{\mu }_i{)}^{?}{\Sigma }_i^{?1}(x?{\mu }_i)\right)$$
此外考慮到相鄰像素深度上的差異性，使用了多尺度BEV進行處理，最后進行上采樣。

實驗結果

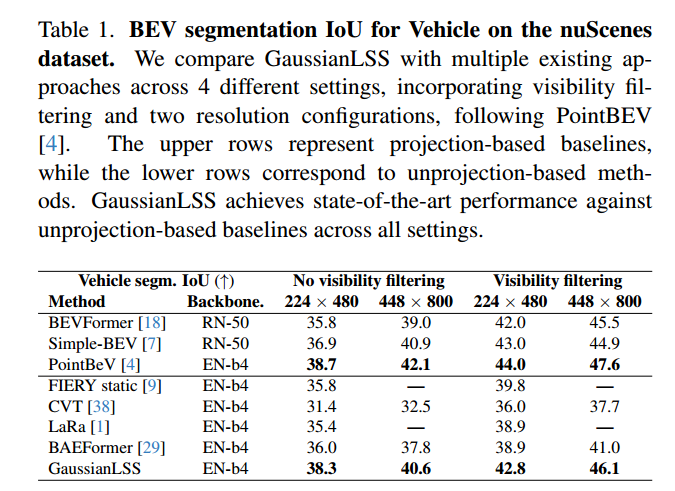
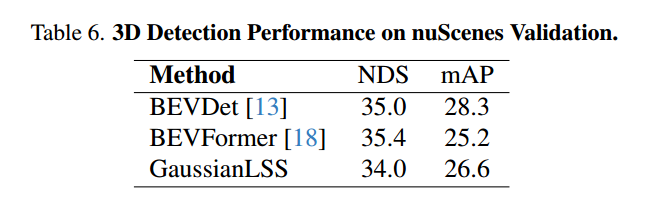
總結

GaussianLSS通過創新性地結合深度不確定性建模與高效的多尺度BEV特征渲染，成功解決了深度模糊性的固有挑戰。這種方法不僅在基于反投影的方法中實現了最先進的性能，還在降低計算資源需求方面表現出色，使其特別適合自動駕駛的實時應用場景。
GaussianLSS的成功證明了顯式不確定性建模在提升空間感知任務性能中的價值，為未來BEV感知系統的發展提供了新的研究方向。