| 2 | 2 | 2 | 1 | 2 | 2 |
| 2 | 2 | 2 | 1 | 2 | 2 |
| 2 | 2 | 2 | 1 | 2 | 2 |
| 3 | 3 | 3 | x | 3 | 3 |
| 2 | 2 | 2 | 1 | 2 | 2 |
| 2 | 2 | 2 | 1 | 2 | 2 |
在平面上有一個點x,再增加一個點,1+1的操作把平面分成了3部分2a1,2a2,2a3,3部分的比值是
| 2a1 | 2a2 | 2a3 |
| 5 | 25 | 5 |
| 0.143 | 0.714 | 0.143 |
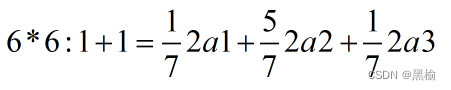
如果平面是正方形,改變平面的尺寸會改變3部分的比值,但是2a1和2a3占比一定同樣多。也就是在正方形的平面上找到2a1和2a3的概率一定是一樣的。
如果希望2a1和2a3出現的概率不一致,一個可能的辦法就是改變平面的形狀,在一個瘦長的錐形區域出現2a1的概率就要大些
| 0 | |||||
| 0 | 2a1 | 15 | 0.714 | ||
| 0 | 2a2 | 5 | 0.238 | ||
| 0 | 2a3 | 1 | 0.048 | ||
| 0 | |||||
| 0 | 0 |
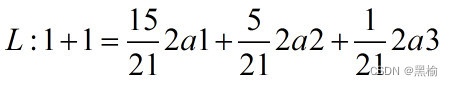
比如在這個L形的區域內,有6*5/2=15個2a1,有5個2a2,有1個2a3占比為71.4%,23.8%,4.8%。2a1>2a2>2a3這意味著在整個L形的區域內找到2a1要容易些。
( A, B )---3*30*2---( 1, 0 )( 0, 1 )
對于二值化二分類網絡,當B全為0時,如果訓練集的圖片數量大于點的數量,迭代次數2a1>2a2>2a3
| n=5 | 迭代次數 | n=4 | 迭代次數 | n=3 | 迭代次數 | |||||||||
| 2a1 | 0 | 0 | 0 | 48757 | - | - | - | 38566.2 | 1 | - | - | 28553.7 | ||
| 0 | 0 | 0 | 48757 | 1 | - | - | 38566.2 | - | - | - | 28553.7 | |||
| 0 | 0 | 0 | 48757 | 1 | - | - | 38566.2 | 1 | - | - | 28553.7 | |||
| 0 | 0 | 1 | 48757 | - | - | - | 38566.2 | |||||||
| 0 | 0 | 1 | 48757 | |||||||||||
| ↓ | ↓ | ↓ | ||||||||||||
| 2a2 | 0 | 0 | 0 | 66503.84 | 1 | - | - | 52243.5 | - | - | - | 37970.4 | ||
| 0 | 0 | 0 | 66503.84 | - | - | - | 52243.5 | - | 1 | - | 37970.4 | |||
| 0 | 0 | 0 | 66503.84 | - | - | - | 52243.5 | 1 | - | - | 37970.4 | |||
| 0 | 1 | 0 | 66503.84 | - | - | 1 | 52243.5 | |||||||
| 0 | 0 | 1 | 66503.84 | |||||||||||
| ↓ | ↓ | ↓ | ||||||||||||
| 2a3 | 0 | 0 | 0 | 85401.86 | - | - | - | 67787.4 | - | - | - | 50456.3 | ||
| 0 | 0 | 0 | 85401.86 | - | - | - | 67787.4 | - | - | - | 50456.3 | |||
| 0 | 0 | 0 | 85401.86 | - | - | - | 67787.4 | 1 | - | 1 | 50456.3 | |||
| 0 | 0 | 0 | 85401.86 | 1 | - | 1 | 67787.4 | |||||||
| 0 | 1 | 1 | 85401.86 | |||||||||||
這和在L形區域內尋找這3個特征的難度剛好是成正比的,尋找的難度越小迭代次數越小。也就是假設所謂收斂過程就是在一個瘦長的錐形區域內,用權重隨機尋找特征結構的過程。因為搜索范圍是一個不對稱的錐形,所以對稱的兩個結構的迭代次數都不同,扁平結構的迭代次數總是更大些。
計算機驗算這組數據,向L形區域內隨機扔2個石子,運行了500,1000,5000次
| 500 | 1000 | 5000 | ||||||
| 2a1 | 350 | 0.7 | 715 | 0.72 | 3571 | 0.71 | ||
| 2a2 | 115 | 0.23 | 239 | 0.24 | 1184 | 0.24 | ||
| 2a3 | 35 | 0.07 | 46 | 0.05 | 245 | 0.05 |
實驗數據和計算數據一致。









并開啟Launchpad活動)









