目錄

1.算法運行效果圖預覽

2.算法運行軟件版本

3.部分核心程序

4.算法理論概述

4.1、DCT變換原理

4.2、基于DCT的圖像壓縮

4.3、基于DCT的圖像解壓縮

5.算法完整程序工程

---

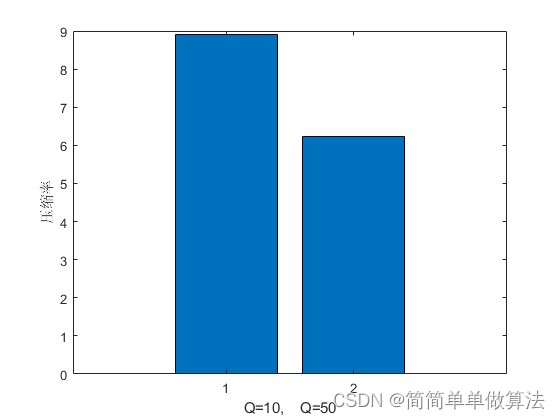
1.算法運行效果圖預覽

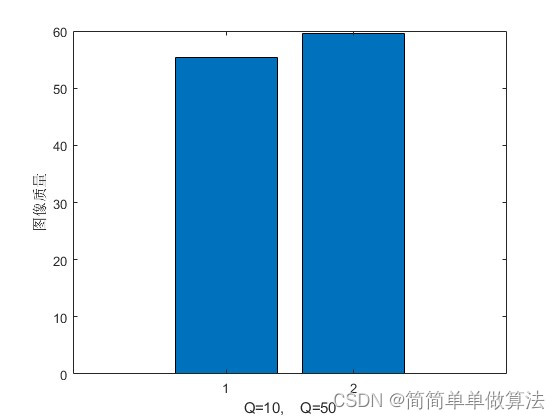
2.算法運行軟件版本

MATLAB2022a

3.部分核心程序

....................................................................
%調用8x8矩陣的量化等級  
load Q10.mat% 對R、G、B通道應用壓縮函數func_ys，得到壓縮后的圖像Rys、Gys、Bys  
Rys  = func_ys(R1,Coff_dct,Q_dct,Bsize);
Gys  = func_ys(G1,Coff_dct,Q_dct,Bsize);
Bys  = func_ys(B1,Coff_dct,Q_dct,Bsize);% 將壓縮后的通道數據合并成一個新的圖像I1ys  
I1ys(:,:,1) = Rys;
I1ys(:,:,2) = Gys;
I1ys(:,:,3) = Bys;
imwrite(I1ys,'TMPS\Iys.jpg');% 將圖像I1ys寫入到文件'TMPS\Iys.jpg'中  % 對壓縮后的圖像應用解壓縮函數func_deys，得到解壓縮后的圖像Rdeys、Gdeys、Bdeys  
Rdeys        = func_deys(Rys,Coff_dct,Q_dct,Bsize);
Gdeys        = func_deys(Gys,Coff_dct,Q_dct,Bsize);
Bdeys        = func_deys(Bys,Coff_dct,Q_dct,Bsize);
% 將解壓縮后的通道數據合并成一個新的圖像I2deys，并轉換為uint8類型  
I2deys(:,:,1) = uint8(Rdeys);
I2deys(:,:,2) = uint8(Gdeys);
I2deys(:,:,3) = uint8(Bdeys);
imwrite(I2deys,'TMPS\Ideys.jpg');% 將圖像I2deys寫入到文件'TMPS\Ideys.jpg'中  % 獲取原始圖像文件和壓縮后的圖像文件的大小（字節） %壓縮率
ys_rate = SIZE1/SIZE2;% 顯示三個圖像：壓縮后的圖像、解壓后的圖像、原始圖像  
figure(1)
subplot(131)
imshow(I1ys);
title('壓縮圖像')
subplot(132)
imshow(I2deys);
title('解壓圖像')
subplot(133)
imshow(I0);
title('原始圖像')I00 = imread('TMPS\Ideys.jpg');
err = (double(I0) - double(I00)) .^ 2;
mse1= sum(err(:)) / (64*64); 
%PSNR 
Max_pixel = 255;
PSNR      = 20*log10((Max_pixel^2)./sqrt(mse1));save R1.mat ys_rate PSNR
00084

4.算法理論概述

? ? ? ?基于DCT（離散余弦變換）的圖像壓縮與解壓縮算法。我們深入探討了DCT變換的原理、其在圖像編碼中的應用，并給出了相應的數學公式和算法實現細節。隨著數字技術的快速發展，圖像數據在日常生活中呈現爆炸性增長。因此，如何有效地壓縮圖像數據，同時確保良好的圖像質量，成為了一個重要的研究課題。DCT變換由于其良好的能量集中特性和與人類視覺系統的匹配度，被廣泛應用于圖像壓縮標準中，如JPEG。

4.1、DCT變換原理

? ? ? 離散余弦變換（DCT）是傅里葉變換的一種變種。它將信號從時域變換到頻域，使得信號的能量大部分集中在幾個頻率分量上。對于圖像而言，DCT可以有效地將圖像的能量集中在左上角的低頻部分。

一維DCT變換公式如下：

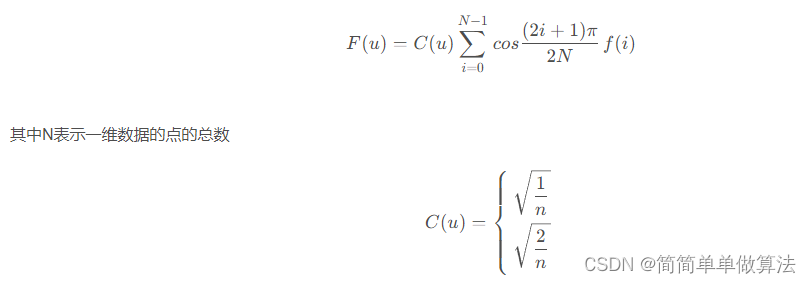
? ? ? 二維DCT變換（通常用于圖像處理）可以通過兩次一維DCT變換實現，首先對行進行變換，再對列進行變換。

? ? ? ? 可以發現，二維DCT變換其實是在一維DCT變換的基礎上，再做一次一維DCT變換。二維DCT也可以寫成矩陣相乘的形式：

? ? ? ? ?二維DCT變換的復雜度達到O(n^4)，所以進行DCT變換的矩陣不宜過大。在實際處理圖片的過程中，需要先把矩陣分塊，一般分為8x8或16x16大小，這樣DCT變換不至于耗費過多的時間。

4.2、基于DCT的圖像壓縮

基于DCT的圖像壓縮主要步驟如下：

分塊：將原始圖像分為8x8或16x16的小塊。
DCT變換：對每個小塊進行二維DCT變換。
量化：使用預定的量化表對DCT系數進行量化，這一步驟是有損的，會丟失部分信息。
編碼：采用Zig-Zag掃描將量化后的系數排列為一維序列，并使用霍夫曼編碼進行進一步壓縮。
通過以上的步驟，我們可以實現圖像的壓縮。需要注意的是，量化步驟是有損的，因此解壓后的圖像與原始圖像會存在一定的差異。

4.3、基于DCT的圖像解壓縮

解壓縮是壓縮的逆過程，主要包括以下步驟：

解碼：使用霍夫曼解碼對編碼后的數據流進行解碼。
反量化：使用與壓縮時相同的量化表對解碼后的數據進行反量化。
反DCT變換：對反量化后的數據進行二維反DCT變換。
重構：將反DCT變換后的塊組合成完整的圖像。

5.算法完整程序工程

OOOOO

OOO

O