1 二叉樹的順序結構

普通的二叉樹是不適合用數組來存儲的，因為可能會存在大量的空間浪費。而完全二叉樹更適合使用順序結構存儲。現實中我們通常把堆(一種二叉樹)使用順序結構的數組來存儲，需要注意的是這里的堆和操作系統虛擬進程地址空間中的堆是兩回事，一個是數據結構，一個是操作系統中管理內存的一塊區域分段

2. 堆的概念及結構

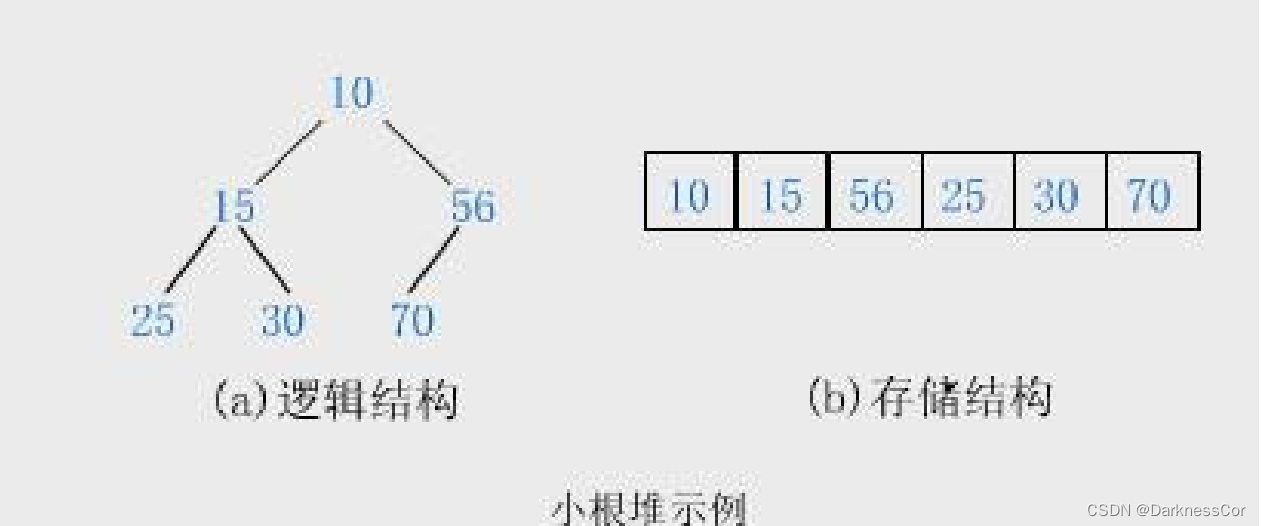
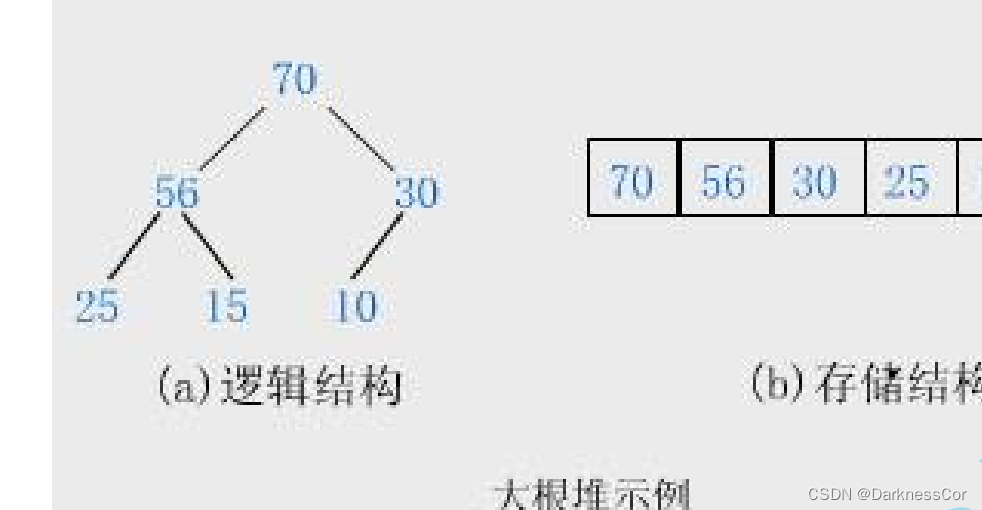
如果有一個關鍵碼的集合K = { ， ， ，…， }，把它的所有元素按完全二叉樹的順序存儲方式存儲在一個一維數組中，并滿足： <= 且 <= ( >= 且 >= ) i = 0，1，
2…，則稱為小堆(或大堆)。將根節點最大的堆叫做最大堆或大根堆，根節點最小的堆叫做最小堆或小根堆。
堆的性質：
1.堆中某個節點的值總是不大于或不小于其父節點的值；
2.堆總是一棵完全二叉樹。

3 .堆的實現(小堆)

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int HPDataType;
typedef struct Heap
{int* a;int size;int capacity;}HP;
void HeapInit(HP* php);
void HeapDestroy(HP* php);
void HeapPush(HP* php, HPDataType x);
// 規定刪除堆頂（根節點）
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
size_t HeapSize(HP* php);
bool HeapEmpty(HP* php);

#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void AdjustUp(HPDataType* a, int child)
{int parent =(child - 1 )/ 2;while (child > 0){if (a[parent] > a[child]){Swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}elsebreak;}}
void AdjustDown(HPDataType* a, int size,int parent)
{int child = parent * 2 + 1;while (child<size){if (child+1<size&&a[child + 1] < a[child]){child++;}if (a[parent] > a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}elsebreak;}}
void HeapInit(HP* php)
{php->a = NULL;php->capacity = 0;php->size = 0;}
void HeapDestroy(HP* php)
{free(php->a);free(php);}
HPDataType HeapTop(HP* php)
{return php->a[0];
}
size_t HeapSize(HP* php)
{return php->size;
}
bool HeapEmpty(HP* php)
{return php->size == 0;
}
void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->capacity == php->size){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);php->a = tmp;php->capacity = newcapacity;}php->a[php->size++] = x;AdjustUp(php->a, php->size-1);}
void HeapPop(HP* php)
{assert(php);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;int parent = 0;AdjustDown(php->a, php->size, 0);}

堆的建立有兩個重要算法即向上調整和向下調整法
堆向下調整算法：現在我們給出一個數組，邏輯上看做一顆完全二叉樹。我們通過從根節點開始的向下調整算法可以把它調整 成一個小堆。向下調整算法有一個前提：左右子樹必須是一個堆，才能調整
向上調整法:
向上調整算法，直到滿足堆。

結尾：今天的分享到此結束，喜歡的朋友如果感覺有幫助可以點贊三連支持，咱們共同進步!