一、噪聲分類
1、高斯噪聲
指服從高斯分布(正態分布)的一類噪聲,其產生的主要原因是由于相機在拍攝時視場較暗且亮度不均勻造成的,同時相機長時間工作使得溫度過高也會引起高斯噪聲,另外電路元器件白身噪聲和互相影響也是造成高斯噪聲的重要原因之一。
概率密度函數(PDF)如下:

初始圖片:

注意加噪聲時,不能直接將 noise+img,不然最終出來的是一片空白和零星幾個噪點,原因在于cv2.imshow輸入要求是 0-1 float 或者 0-255 int。
代碼:
import cv2
import random
import numpy as np
img = cv2.imread('A.png')# 產生高斯隨機數
noise = np.random.normal(0,50,size=img.size).reshape(img.shape[0],img.shape[1],img.shape[2])
# 加上噪聲
img = img + noise
img = np.clip(img,0,255)
img = img/255 cv2.imshow('Gauss noise',img)
cv2.waitKey(0)
3)高斯濾波
高斯濾波是一種線性平滑濾波,一般用于消除高斯噪聲。對于每一個像素點的值,是由其本身和鄰域內的其他像素值經過加權平均后得到。
二維高斯函數:

具體過程:
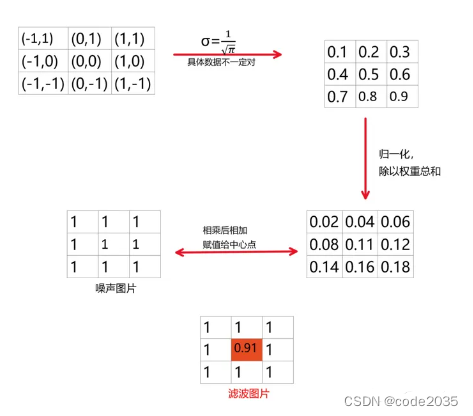
代碼:使用cv2.GaussianBlur()函數

注意高斯模糊半徑不能為偶數
濾波結果:

2、泊松噪聲
簡言之就是符合泊松分布的噪聲模型,又稱散粒噪聲。
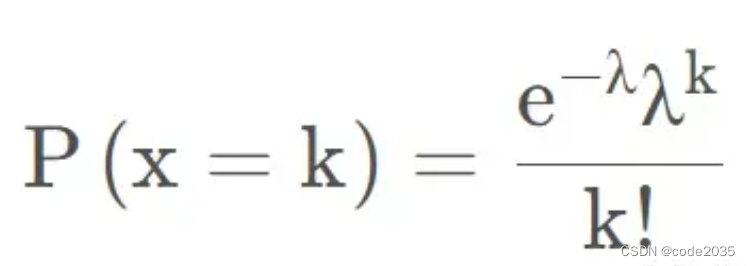
使用**np.random.poisson()**函數
import cv2
import random
import numpy as np
img = cv2.imread('A.png')# 產生泊松噪聲
noise = np.random.poisson(lam=20,size=img.shape).astype('uint8')# 加上噪聲
img = img + noise
np.clip(img,0,255)
img = img/255cv2.imshow('Poisson noise',img)
cv2.waitKey(0)
λ值越大,噪聲程度越深。
3、椒鹽噪聲
椒鹽噪聲又稱為脈沖噪聲,是在圖像上隨機出現黑色白色的像素,顧名思義就是椒鹽噪聲 = 椒噪聲(值為0,黑色) + 鹽噪聲(值為255,白色)
直接上代碼:
import cv2
import random
import numpy as np
img = cv2.imread('A.png')# 轉化成向量
x = img.reshape(1,-1)
# 設置信噪比
SNR = 0.85
# 得到要加噪的像素數目
noise_num = x.size * (1-SNR)
# 得到需要加噪的像素值的位置
list = random.sample(range(0,x.size),int(noise_num))for i in list:if random.random() >= 0.5:x[0][i] = 0else:x[0][i] = 255
img1 = x.reshape(img.shape)cv2.imshow('salt&pepper noise',img1)
cv2.waitKey(0)
SNR越小,噪聲越大。
4、瑞利噪聲
一般是由由信道不理想引起的,它與信號的關系是相乘,信號在它在,信號不在他也就不在。
瑞利密度對傾斜形狀直方圖的建模非常有用。
在生成瑞利噪聲的時候,其實采用的是**np.random.rayleigh()** 方法生成,而這個方法就是根據第二個公式來的,所以只需要指定1個參數,得到的分布和第一個公式相比本質是相同的。
代碼:
import cv2
import random
import numpy as np
img = cv2.imread('A.png')# 產生瑞利噪聲
sigma = 70.0
noise = np.random.rayleigh(sigma, size=img.shape)
# 可以試試下面這個效果
# noise = np.random.rayleigh(img, size=img.shape)# 加上噪聲
img = img + noise
np.clip(img,0,255)
img = img/255cv2.imshow('Rayleigh noise',img)
cv2.waitKey(0)
print(img.shape)
5、愛爾蘭(伽馬)噪聲
概率密度函數(PDF)如下:(b是一個正整數)
指數分布和卡方分布其實可以看成是伽馬分布的特殊形式。
b = 1時:指數分布;
b =n/2,a = 1/2時:卡方分布。
代碼:
noise = np.random.gamma(shape=10.0,scale=10.0,size=img.shape)
#其他部分同上
6、均勻噪聲
noise = np.random.uniform(50,100,img.shape)
#其他部分同上
二、去噪方法
1、均值濾波
1.1 算術平均濾波

import cv2
import random
import numpy as np
img = cv2.imread('A.png')# 產生高斯隨機數
noise = np.random.normal(0,50,size=img.size).reshape(img.shape[0],img.shape[1],img.shape[2])
# 加上噪聲
img = img + noise
img = np.clip(img,0,255)
img = img/255 # 算術平均濾波
img1 = np.transpose(img,(2,0,1)) #轉換成[channel,H,W]形式
m = 3 #定義濾波核大小
n = 3
rec_img = np.zeros((img1.shape[0],img1.shape[1]-m+1,img1.shape[2]-n+1))
for channel in range(rec_img.shape[0]):for i in range(rec_img[channel].shape[0]):for j in range(rec_img[channel].shape[1]):rec_img[channel][i,j] = img1[channel][i:i+m,j:j+n].sum()/(m*n)
rec_img = np.transpose(rec_img,(1,2,0))cv2.imshow('average',rec_img)
cv2.waitKey(0)具體過程可以配合下圖理解

去噪效果:

1.2 幾何均值濾波
import cv2
import random
import numpy as np
img = cv2.imread('A.png')# 產生高斯隨機數
noise = np.random.normal(0,50,size=img.size).reshape(img.shape[0],img.shape[1],img.shape[2])
# 加上噪聲
img = img + noise
img = np.clip(img,0,255)
img = img/255 # 幾何均值濾波
img1 = np.transpose(img,(2,0,1)) #轉換成[channel,H,W]形式
m = 3 #定義濾波核大小
n = 3
rec_img = np.zeros((img1.shape[0],img1.shape[1]-m+1,img1.shape[2]-n+1))
for channel in range(rec_img.shape[0]):for i in range(rec_img[channel].shape[0]):for j in range(rec_img[channel].shape[1]):rec_img[channel][i,j] = np.power(np.prod(img1[channel][i:i+m,j:j+n]),1/(m*n))
rec_img = np.transpose(rec_img,(1,2,0))cv2.imshow('average',rec_img)
cv2.waitKey(0)去噪效果:
幾何均值濾波對0值是非常敏感,缺陷也很明顯,那就是當窗口內像素只要有一個值為0,則其計算得到的值就是0。
1.3 諧波平均濾波
rec_img[channel][i,j] = 1/(np.power(img1[channel][i:i+m,j:j+n],-1).sum())*(m*n)
# 其余部分同上
該方法既能處理鹽粒噪聲,又能處理類似于于高斯噪聲的其他噪聲,但是不能處理胡椒噪聲
2、統計排序濾波
2.1 中值濾波
我們非常熟悉的一種去噪方法,它是用像素鄰域中的灰度中值來代替像素的值。
代碼:
import cv2
import random
import numpy as np
img = cv2.imread('A.png')# 產生高斯隨機數
noise = np.random.normal(0,50,size=img.size).reshape(img.shape[0],img.shape[1],img.shape[2])
# 加上噪聲
img = img + noise
img = np.clip(img,0,255)
img = img/255 # 中值濾波
img1 = np.transpose(img,(2,0,1)) #轉換成[channel,H,W]形式
m = 3 #定義濾波核大小
n = 3
rec_img = np.zeros((img1.shape[0],img1.shape[1]-m+1,img1.shape[2]-n+1))
for channel in range(rec_img.shape[0]):for i in range(rec_img[channel].shape[0]):for j in range(rec_img[channel].shape[1]):rec_img[channel][i,j] = np.median(img1[channel][i:i+m,j:j+n])
rec_img = np.transpose(rec_img,(1,2,0))cv2.imshow('median',rec_img)
cv2.waitKey(0)去噪效果:
或者直接使用cv2.medianBlur()函數
import cv2
import random
import numpy as np
img = cv2.imread('A.png')# 產生高斯隨機數
noise = np.random.normal(0,50,size=img.size).reshape(img.shape[0],img.shape[1],img.shape[2])
# 加上噪聲
img = img + noise
img = np.clip(img,0,255)
img = np.uint8(img)# 中值濾波
rec_img = cv2.medianBlur(img,3)cv2.imshow('median',rec_img)
cv2.waitKey(0)2.2 最大值和最小值濾波
代碼:
rec_img[channel][i,j] = (np.amax(img1[channel][i:i+m,j:j+n]) + np.amin(img1[channel][i:i+m,j:j+n]))/2對高斯噪聲處理的濾波效果:

2.4 修正阿爾法均值濾波
處理方法:在鄰域 S x y S_{xy} Sxy? 內刪除 d / 2 d/2 d/2個最低灰度值和 d / 2 d/2 d/2個最高灰度值。 g R ( r , c ) g_{R}(r,c) gR?(r,c)表示 S x y S_{xy} Sxy? 中剩下的 m n ? d mn-d mn?d個像素。
d = 0 d=0 d=0: 變成算術平均濾波
d = m n ? 1 d=mn-1 d=mn?1:中值濾波
代碼:
import cv2
import random
import numpy as np
img = cv2.imread('A.png')# 產生高斯隨機數
noise = np.random.normal(0,50,size=img.size).reshape(img.shape[0],img.shape[1],img.shape[2])
# 加上噪聲
img = img + noise
img = np.clip(img,0,255)
img = img/255 # 修正阿爾法均值濾波
img1 = np.transpose(img,(2,0,1)) #轉換成[channel,H,W]形式
m = 3 #定義濾波核大小
n = 3
d = 4 #d取偶數
rec_img = np.zeros((img1.shape[0],img1.shape[1]-m+1,img1.shape[2]-n+1))
for channel in range(rec_img.shape[0]):for i in range(rec_img[channel].shape[0]):for j in range(rec_img[channel].shape[1]):img2 = np.sort(np.ravel(img1[channel][i:i+m,j:j+n])) #np.ravel():多維數組變成一維數組rec_img[channel][i,j] = (img2[int(d/2):-int(d/2)].sum())*(1/(m*n-d))
rec_img = np.transpose(rec_img,(1,2,0))cv2.imshow('alpha average',rec_img)
cv2.waitKey(0)去噪效果:




)




)
)
)





)


