目錄

組合問題

leetcode77題.組合

leetcode216題.組合總和III

leetcode40題.組合總和II

leetcode39題.組合總和

---

倘若各位不太清楚回溯算法可以去看我上一篇文章。

回溯算法詳解-CSDN博客

組合問題

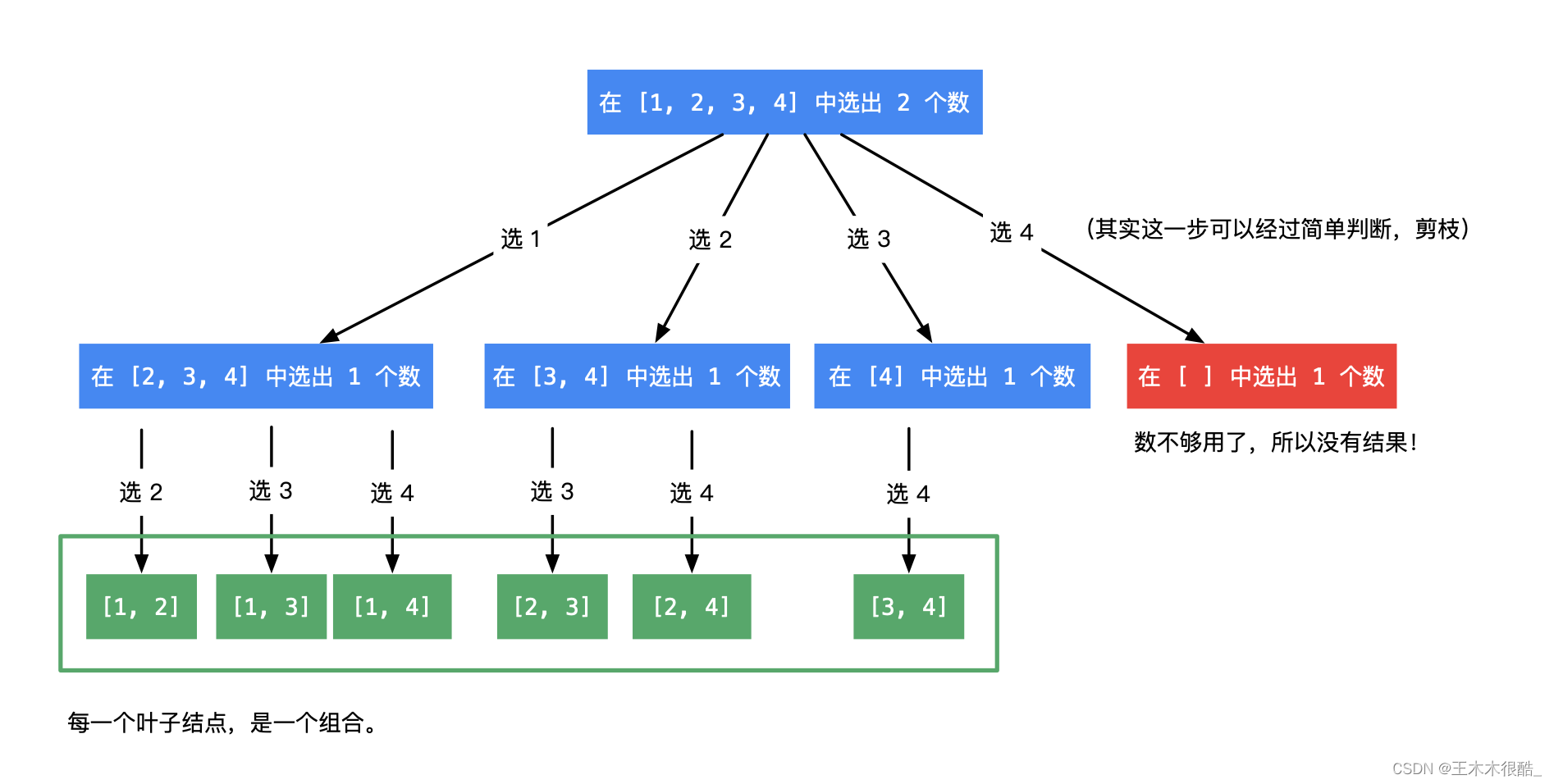
一般組合和排列類的問題我們都會轉化成一個樹形問題，更便于理解。

leetcode77題.組合

77. 組合 - 力扣（LeetCode）

題目：給定兩個整數 n 和 k，返回范圍 [1, n] 中所有可能的 k 個數的組合。

你可以按 任何順序 返回答案。

示例 1：

輸入：n = 4, k = 2
輸出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

class Solution {// 創建存放結果集List<List<Integer>> res = new ArrayList<>();// 存放單個子集List<Integer> temp = new ArrayList<>();public List<List<Integer>> combine(int n, int k) {backTrace(n, k , 1);//index從1開始選，之后選2、選3return res;}//一般回溯操作沒有返回值，index表示我們選到了哪里，比如我們選到了1、2、3void backTrace(int n, int k, int index){// 優化：稱之為剪枝，看能否有k個元素可以選//選進去的元素 + 可選元素 < kif(temp.size() + (n - index + 1) < k){return;}// 結束條件：我們已經選了k個元素if(temp.size() == k){res.add(new ArrayList<>(temp));return;}// 從多個元素中逐一選擇，從index到n就是我們的可選子集for(int i = index; i <= n; i++){// 選元素進行處理，比如選了1temp.add(i);// 繼續下一層，即2、3、4backTrace(n, k, i + 1);// 撤銷我們處理過的元素temp.remove(temp.size() - 1);}}
}

leetcode216題.組合總和III

216. 組合總和 III - 力扣（LeetCode）

找出所有相加之和為?n?的?k?個數的組合，且滿足下列條件：

• 只使用數字1到9
• 每個數字最多使用一次

返回?所有可能的有效組合的列表?。該列表不能包含相同的組合兩次，組合可以以任何順序返回。

示例 1:

輸入: k = 3, n = 7
輸出: [[1,2,4]]
解釋:
1 + 2 + 4 = 7
沒有其他符合的組合了。

class Solution {//保存最終的結果List<List<Integer>> res = new ArrayList<>();//臨時的保存每一組成立的結果List<Integer> temp = new ArrayList<>();public List<List<Integer>> combinationSum3(int k, int n) {backTrace(n, k, 1, 0);return res;}void backTrace(int n, int k, int index, int sum){// 優化剪枝if(sum > n){return;}//湊不到k個數-> 可選的數 + 已選的數 < kif((9 - index + 1) + temp.size() < k){return;}// 結束條件：已經選了k個數if(temp.size() == k){if(sum == n){res.add(new ArrayList<>(temp));}return;}// 回溯for(int i = index; i <= 9; i++){// 選其中一個元素temp.add(i);sum = sum + i;backTrace(n, k, i + 1, sum);// 撤銷處理temp.remove(temp.size() - 1);sum = sum - i;}}
}

leetcode40題.組合總和II

40. 組合總和 II - 力扣（LeetCode）

給定一個候選人編號的集合?candidates?和一個目標數?target?，找出?candidates?中所有可以使數字和為?target?的組合。

candidates?中的每個數字在每個組合中只能使用一次 。

注意：解集不能包含重復的組合。

示例 1:

輸入: candidates = [10,1,2,7,6,1,5], target = 8,
輸出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

class Solution {//存結果的結果集List<List<Integer>> res = new ArrayList<>();//臨時變量存子集List<Integer> temp = new ArrayList<>();public List<List<Integer>> combinationSum2(int[] candidates, int target) {Arrays.sort(candidates);//給數組排序backTrack(candidates, target, 0, 0);//index表示數組下標，從0開始return res;}/*怎么處理重復的組合1. 排序 [1, 1, 5, 6, 7, 10];*/void backTrack(int[] candidates, int target, int index, int sum){//剪枝if(sum > target){return;}// 結束條件if(sum == target){res.add(new ArrayList<>(temp));return;}// 處理主要邏輯for(int i = index; i < candidates.length; i++){// 遇到重復的數就跳過，去掉重復的組合if(i > index && candidates[i] == candidates[i-1]){continue;}// 從多個元素選擇一個temp.add(candidates[i]);sum = sum + candidates[i];backTrack(candidates, target, i + 1, sum);// 撤銷之前的操作temp.remove(temp.size() - 1);sum = sum - candidates[i];}}
}

leetcode39題.組合總和

39. 組合總和 - 力扣（LeetCode）

給你一個 無重復元素 的整數數組 candidates 和一個目標整數 target ，找出 candidates 中可以使數字和為目標數 target 的 所有 不同組合 ，并以列表形式返回。你可以按 任意順序 返回這些組合。

candidates 中的 同一個 數字可以 無限制重復被選取 。如果至少一個數字的被選數量不同，則兩種組合是不同的。

對于給定的輸入，保證和為 target 的不同組合數少于 150 個。

示例 1：

輸入：candidates = [2,3,6,7], target = 7
輸出：[[2,2,3],[7]]
解釋：
2 和 3 可以形成一組候選，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一個候選， 7 = 7 。
僅有這兩種組合。?

class Solution {//存取結果List<List<Integer>> res = new ArrayList<>();//臨時存取子集List<Integer> temp = new ArrayList<>();public List<List<Integer>> combinationSum(int[] candidates, int target) {backTrack(candidates, target, 0, 0);return res;}void backTrack(int[] candidates, int target, 0int index, int sum){// 剪枝if(sum > target){return;}// 結束條件if(sum == target){res.add(new ArrayList<>(temp));return;}// 處理主要邏輯for(int i = index; i < candidates.length; i++){// 從多個元素選擇一個temp.add(candidates[i]);sum = sum + candidates[i];//可以重復選擇i，所以不用i+1backTrack(candidates, target, i, sum);// 撤銷之前的操作temp.remove(temp.size() - 1);sum = sum - candidates[i];}}
}