思維導圖

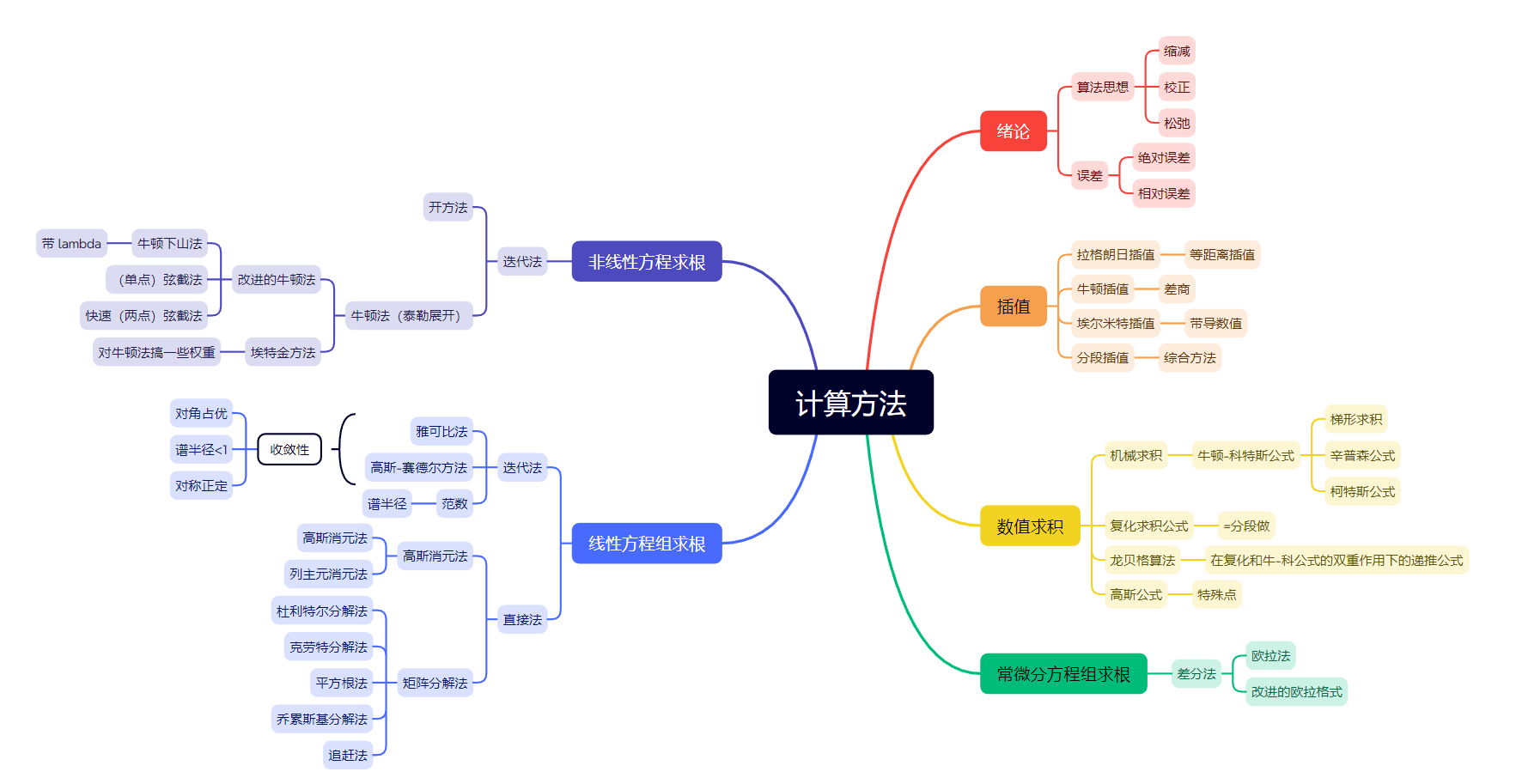
緒論

算法的性質：
有窮性、確切性、有輸入輸出、可行性
算法的描述方法：
自然語言、偽代碼、流程圖、N-S流程圖
算法設計思想：

• 化大為小的縮減技術：二分法
• 化難為易的校正技術：開方法
• 化粗為精的松弛技術：加權平均 超松弛 割圓術

誤差來源：

• 模型/描述誤差
• 觀測誤差
• 舍入如茶
• 初值誤差

計算方法只研究后兩類誤差

誤差的度量：
絕對誤差$e(x^{?})=x?x^{?}$
絕對誤差限$|e(x^{?})|=|x?x^{?}|<\epsilon$
相對誤差$e_r(x^{?})=e(x^{?})/x\approx e(x^x)/x^{?}$
相對誤差限
有效數字：
$x^{?}=10^m?x_1{x}_2{x}_3....x_p$
$|e|<=0.5?10^{m?n}$，則具有n位有效數字
$x^{?}$準確到末位時，稱有效數

選擇算法原則：

• 避免相近的數相減
• 避免很小的數作分母
• 避免大數淹沒小數
• 選用穩定性好的算法

插值

用多項式替代真實函數，該多項式存在且唯一（克萊姆法則證明）

拉格朗日插值

$L_n(x)={\sum }_{i=0}^n{\phi }_i(x)y_i={\sum }_{i=0}^n({\prod }_{j=0,j!=i}^n\frac{x?x_j}{x_i?x_j})y_i$
其中，$\phi (x)$是插值基函數
本質上拉格朗日插值函數是加權和
特點：

• 插值點需要等距
• 新點進入需要重新計算基函數
• 高次插值的精度不一定高，可能產生龍格現象

牛頓插值

差商：
零階差商：$f(x_i)=y_i$
一階差商：$f(x_i,x_j)=\frac{f(x_j)?f(x_i)}{x_j?x_i}$
二階差商：$f(x_i,x_j,x_k)=\frac{f(x_j,x_k)?f(x_i,x_j)}{x_k?x_i}$
可用表格法計算差商，對角線上的是系數
牛頓插值多項式：
$p_n(x)=f(x_0)+f(x_0,x_1)(x?x_0)+...+f(x_0,x_1,...,x_n)(x?x_0)(x?x_1)...(x?x_{n?1})$
特點：

• 和拉格朗日插值結果一致
• 不需要重新計算基函數
• 不需要插值點等距

埃米爾特Hermite插值（切觸插值）

兩點三次插值：
$p_3(x)=y_0{\phi }_0(x)+y_1{\phi }_1(x)+y_0^{\prime }{\psi }_0(x)+y_1^{\prime }{\psi }_1(x)$
其中${\phi }_0(x)=(1+2\frac{x?x_0}{x_1?x_0})(\frac{x?x_1}{x_0?x_1}{)}^2$
${\phi }_1(x)=(1+2\frac{x?x_1}{x_0?x_1})(\frac{x?x_0}{x_1?x_0}{)}^2$
${\psi }_0(x)=(x?x_0)(\frac{x?x_0}{x_0?x_1}{)}^2$
${\psi }_1(x)=(x?x_1)(\frac{x?x_0}{x_1?x_0}{)}^2$
特點：

• 具有導數值

分段插值

大一統的方法，在段內，想用哪種插就用哪種插！

數值積分

正統方法是牛頓-萊布尼茨公式，但是我們又算不出來，不想算，咋辦呢

代數精度

一個公式，對于不超過m次的任意多項式都準確，但對m+1次有不準確的，那么具有m階代數精度。
簡化一下，用1，x，$x^2$往里帶就行

機械求積

${\int }_a^{b}f(x)dx=(b?a){\sum }_{i=0}^n{\lambda }_{i}f(x_i)$ 加權和

梯形求積公式

${\int }_a^{b}f(x)dx=(b?a)/2(f(a)+f(b))$

牛頓-科特斯公式

將求積區間[a,b]劃分為n等分，用等分點構造拉格朗日插值，用L(x)代替f(x)

n	求積系數1	求積系數2	求積系數3	求積系數4	求積系數5
1	1/2	1/2
2	1/6	4/6	1/6
3	1/8	3/8	3/8	1/8
4	7/90	16/45	2/15	16/45	7/90

其中n=1為梯形求積公式，n=2為辛普森公式，n=4為科特四公式
奇數的代數精度和前一個偶數一樣，所以正常人沒人用奇數的
代數精度分別為1，3，3，5

復化求積公式

跟分段插值一樣
復化梯形：$I=\frac{b?a}{2n}(f(a)+2{\sum }_{i=1}^{n?1}f(x_i)+f(b))$
復化辛普森公式：$I=\frac{b?a}{6n}(f(a)+4{\sum }_{i=0}^{n?1}f(x_{i+1/2})+2{\sum }_{i=1}^{n?1}f(x_i)+f(b))$
復化柯特斯公式：$I=\frac{b?a}{90n}(f(a)+32{\sum }_{i=0}^{n?1}f(x_{i+1/4})+12{\sum }_{i=0}^{n?1}f(x_{i+1/2})+32{\sum }_{i=0}^{n?1}f(x_{i+3/4})+14{\sum }_{i=1}^{n?1}f(x_i)+7f(b))$

龍貝格算法(kao)?

$T_1=(b?a)/2(f(a)+f(b))$ 一個梯形
$T_{2n}=1/2T_1+2/h{\sum }_{i=0}^{n?1}f(x_{i+1/2})$
$S_n=4/3T_{2n}?1/3T_n$
$C_n=16/15S_{2n}?1/15S_n$
$R_n=64/63C_{2n}?1/63C_n$

高斯公式

求積節點不是等分，而是一些特殊點
${\int }_a^{b}f(x)dx=\frac{b?a}{2}{\int }_{?1}^{1}g(t)dt$，見資料積分區間轉換
一點：${\int }_{?1}^{1}f(x)dx\approx 2f(0)$
兩點：${\int }_{?1}^{1}f(x)dx\approx f(?\frac{1}{\sqrt{3}})+f(\frac{1}{\sqrt{3}})$
三點：${\int }_{?1}^{1}f(x)dx\approx \frac{5}{9}f(?\sqrt{\frac{3}{5}})+\frac{8}{9}f(0)+\frac{5}{9}f(\sqrt{\frac{3}{5}})$
一般積分區間的高斯公式

方程求根的迭代法

$x_{k+1}=\phi (x_k)$
導數的絕對值<=1時，收斂

開方算法

$x_0>0$
$x_{k+1}=\frac{1}{2}(x_k+\frac{a}{x_k})$

牛頓法（重點）

泰勒展開前兩項，得到$x_{k+1}=x_k?\frac{f(x_k)}{f^{\prime }(x_k)}$
使用條件：

• 介值定理
• f’(x)!=0
• f’'(x)存在且不變號
• x0選點必須使得f’'(x)f(x0)>0

如此才能收斂

收斂速度

$\frac{e_{k+1}}{e_k^p}$->C 則迭代過程是p階收斂的
牛頓法為平方收斂

牛頓下山法

要求|函數值|單調下降
得到$x_{k+1}=x_k?\lambda \frac{f(x_k)}{f^{\prime }(x_k)}$
$0<\lambda <1$，稱下山因子，逐步探索下山因子，從1開始，如果有一步始終找不到，則重選初值

（單點）弦截法

令$f^{\prime }(x_k)\approx \frac{f(x_k)?f(x_0)}{x_k?x_0}$，用割線代替切線

快速/兩點 弦截法

需要兩個初值x0和x1

埃特金迭代公式

$\overline{x_{k+1}}=\phi (x_k)$ 牛頓一次
$\widetilde{x_{k+1}}=\phi (\overline{x_{k+1}})$ 再牛頓一次
$x_{k+1}=\widetilde{x_{k+1}}?\frac{(\widetilde{x_{k+1}}?\overline{x_{k+1}}{)}^2}{\widetilde{x_{k+1}}?2\overline{x_{k+1}}+x_k}$ 奇怪的加權！

線性方程組的迭代法

Jacobi

$x_{k+1}=?D^{?1}(L+U)x+D^{?1}b$
移過去，用xk算

Gauss-Seidel

$x_{k+1}=?(D+L{)}^{?1}Ux+(D+L{)}^{?1}b$
移過去，用$x_{k+1}$算

收斂判斷

Jacobi迭代法和Gauss-Seidel迭代法的收斂性

范數

向量的1范數=x絕對值之和
2范數=歐氏距離
無窮范數=絕對值的最大值

矩陣的1范數是列范數，對每列的絕對值求和，找個最大的列
2范數是譜范數 $||A|{|}_2=\sqrt{{\lambda }_{max}(A^{T}A)}$
無窮范數是行范數，也許因為它是橫著的吧(?

譜半徑：A絕對值最大的特征值
對任意矩陣范數，譜半徑都<=范數，所以范數要是<1，迭代法是不是就必然收斂了呢~

線性方程組的直接法

高斯消元法

化成上下三角形，這也要說？

列主元消元法

換行再消元

矩陣分解法

可以分解為LU 一個下三角和一個上三角的乘積，其中一個是單位的

• Doolittle分解法
  先橫著算u，再豎著算l
• crout分解法
  先豎著算l，再橫著算u

有公式但是記不住，現推吧

• 平方根法分解 A=$L{L}^T$ 有公式
• Cholesky分解 正定矩陣分解為$A=LD{L}^T$代價<平方根
• 追趕法 三對角矩陣適用 消元+回代

常微分方程的差分法

歐拉格式

向前的$y(x_{n+1})\approx y(x_n)+hf(x_n,y(x_n))$
向后的（隱式）$y(x_{n+1})\approx y(x_n)+hf(x_{n+1},y(x_{n+1}))$
兩步$y(x_{n+1})\approx y_{n?1}+2hf(x_n,y(x_n))$ 無法直接啟動
梯形格式 $y(x_{n+1})\approx \frac{h}{2}(f(x_n,y(x_n))+f(x_{n+1},y(x_{n+1}))$這也是隱式的，也沒法用（二階）

改進的歐拉格式

二階代數精度
先預報，再校正
預報值$\overline{y(x_{n+1})}=y(x_n)+hf(x_n,y(x_n))$
校正值$y(x_{n+1})\approx y(x_n)+\frac{h}{2}(f(x_n,y(x_n))+f(x_{n+1}\overline{y(x_{n+1})})$
可以簡化表示為：