時間序列分析是一種用于研究隨時間變化的數據模式和趨勢的統計方法。這類數據通常按照時間順序排列，例如股票價格、氣溫、銷售額等。時間序列分析的目標是從過去的觀測中提取信息，以便預測未來的趨勢。

以下是關于時間序列分析的一些重要概念、模型檢驗方法以及應用：

1. 概念：

   • 趨勢（Trend）： 時間序列中長期的運動趨勢，表示數據隨時間變化的整體方向。
   • 季節性（Seasonality）： 時間序列中短期的周期性波動，可能由季節、月份等因素引起。
   • 周期性（Cyclical）： 時間序列中的長期周期性波動，通常不是固定的時間間隔。
   • 噪聲（Noise）： 隨機的、不規律的波動，表示不能歸因于趨勢、季節性或周期性的隨機變動。

2. 常見的時間序列分析模型：

   • 移動平均模型（Moving Average, MA）： 通過計算一定時間范圍內的均值來平滑時間序列數據。
   • 指數平滑模型（Exponential Smoothing, ES）： 根據過去觀測的加權平均值來預測未來觀測。
   • 自回歸模型（Autoregressive, AR）： 用過去的觀測值來預測未來的觀測值。
   • 自回歸滑動平均模型（Autoregressive Integrated Moving Average, ARIMA）： 結合了AR和MA模型，同時考慮了差分項，用于處理非平穩時間序列。

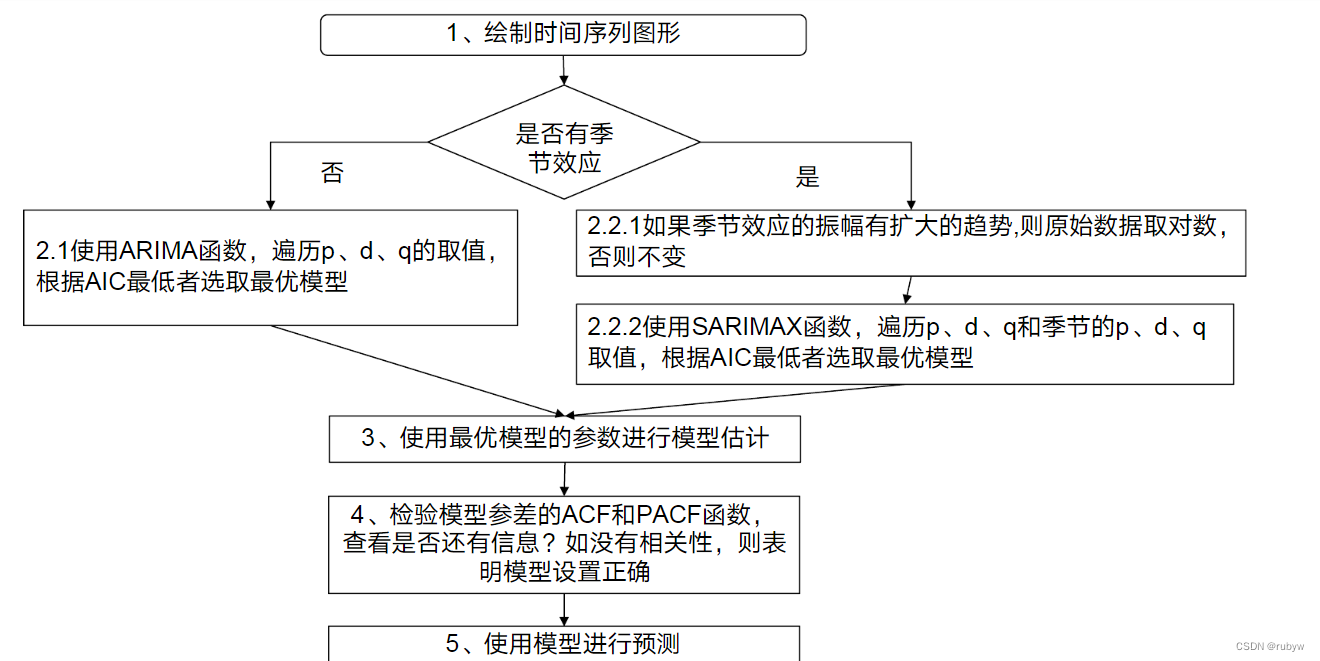
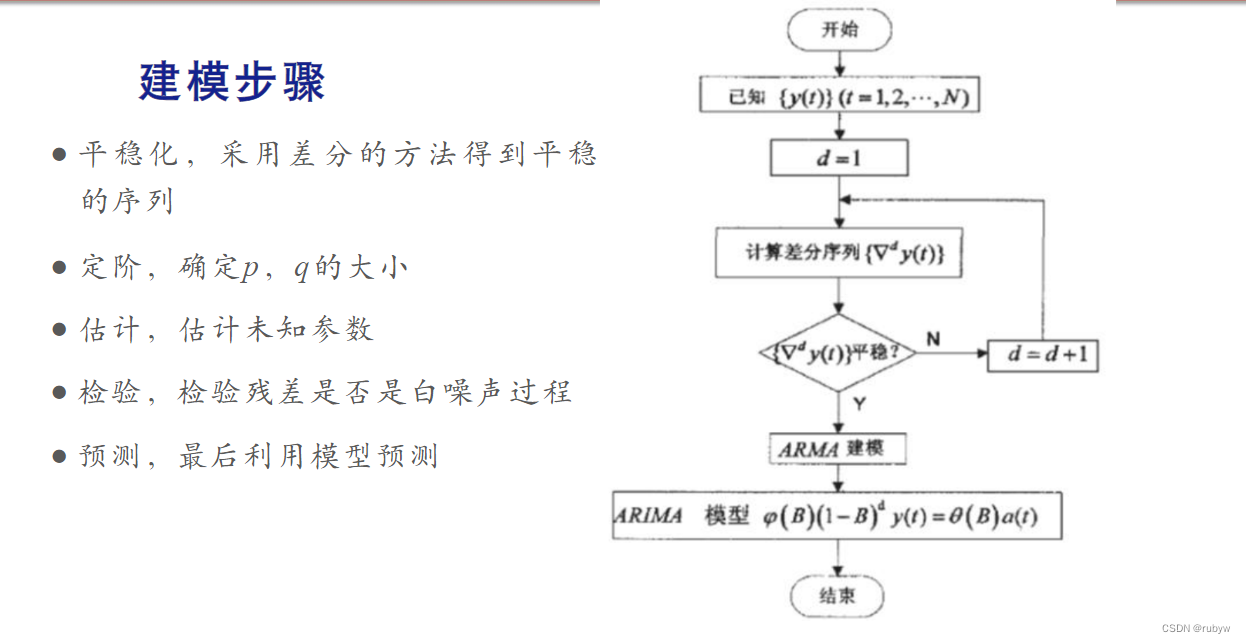
ARIMA（Autoregressive Integrated Moving Average）模型是一種常用于處理平穩和非平穩時間序列的模型。ARIMA模型的三個組成部分分別是自回歸項（AR）、差分項（I）和移動平均項（MA）。ARIMA(p, d, q)中，p表示自回歸階數，d表示差分階數，q表示移動平均階數。

對于包含季節性的時間序列，進行季節性調整可以使得分析更為準確。常見的季節性調整方法包括X-12-ARIMA、季節性分解法和回歸法。

3. 模型檢驗方法：

   • 殘差分析： 檢查模型的殘差是否具有隨機性，即是否存在未被模型捕捉的模式。
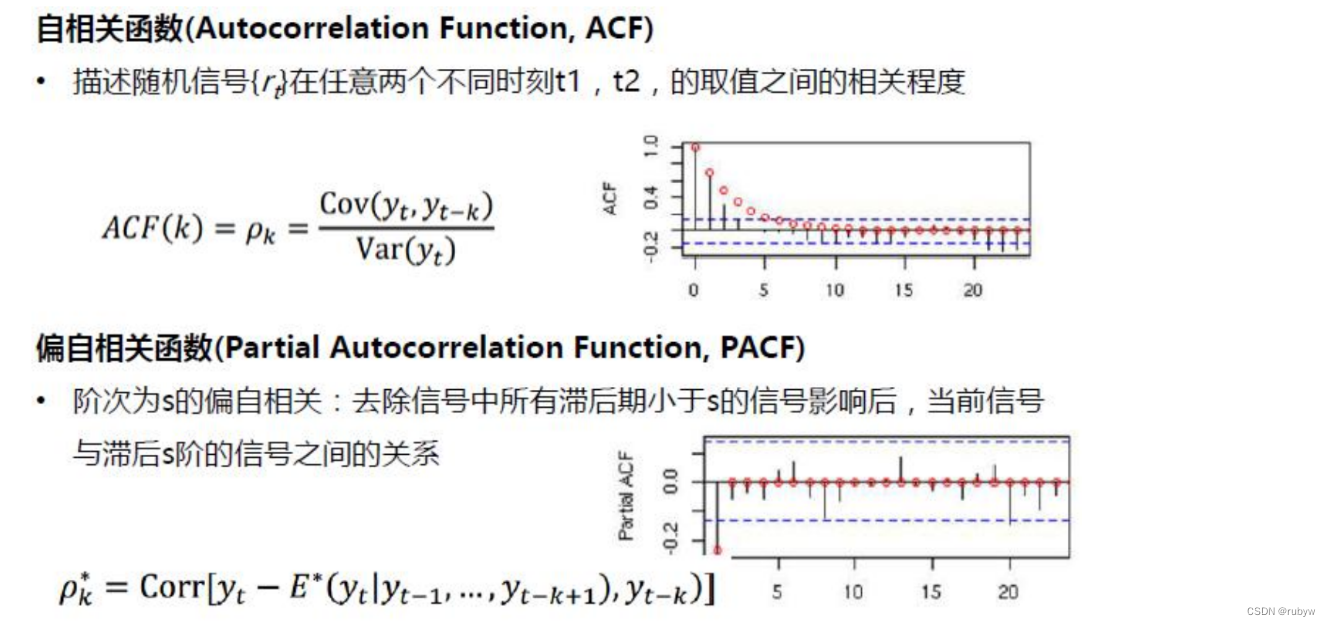
   • Ljung-Box檢驗： 用于檢驗序列的自相關是否顯著，從而判斷是否存在未被模型捕捉的信息。
   • 走勢圖和自相關圖： 可視化工具，用于檢查數據的趨勢和自相關性,觀察預測結果和殘差是否符合模型假設。
   • 均方根誤差（Root Mean Squared Error, RMSE）： 衡量模型預測與實際觀測之間的差異。
   • 平均絕對百分比誤差（Mean Absolute Percentage Error, MAPE）： 衡量預測誤差的百分比。

4. 應用領域：

   • 金融領域： 預測股票價格、匯率等金融指標的走勢。
   • 銷售預測： 預測產品銷售量，幫助制定庫存和生產計劃。
   • 氣象學： 預測氣溫、降雨量等氣象變量。
   • 運輸和物流： 優化運輸路線、預測貨物需求。
   • 醫學： 預測疾病傳播趨勢、患者數量等。

在實際應用中，選擇合適的模型和檢驗方法取決于數據的性質和特點，以及分析的具體目的。不同的行業和領域可能需要使用不同的時間序列分析工具和技術。