1、數倉實施過程

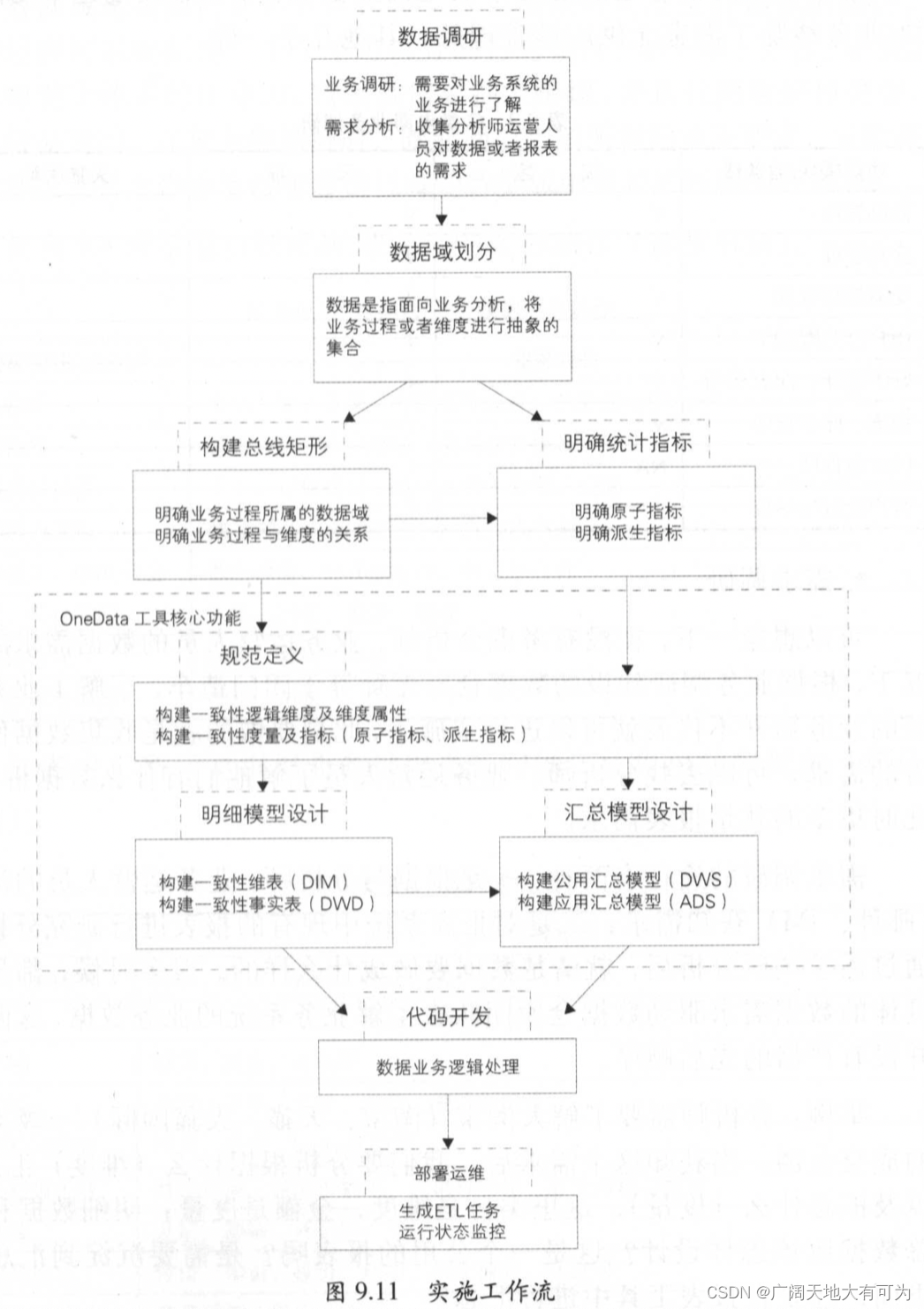
1.1 數據調研

????????數據調研包括：業務調研、需求調研

???????業務調研

????????????????需要調研企業內有哪些業務線、業務線的業務是否還有相同點和差異點

? ? ? ? ? ? ? ? 各個業務線有哪些業務模塊，每個模型下有哪些業務流程，每個流程下產生的數據

? ? ? ? ? ? ? ? 是怎樣存儲的

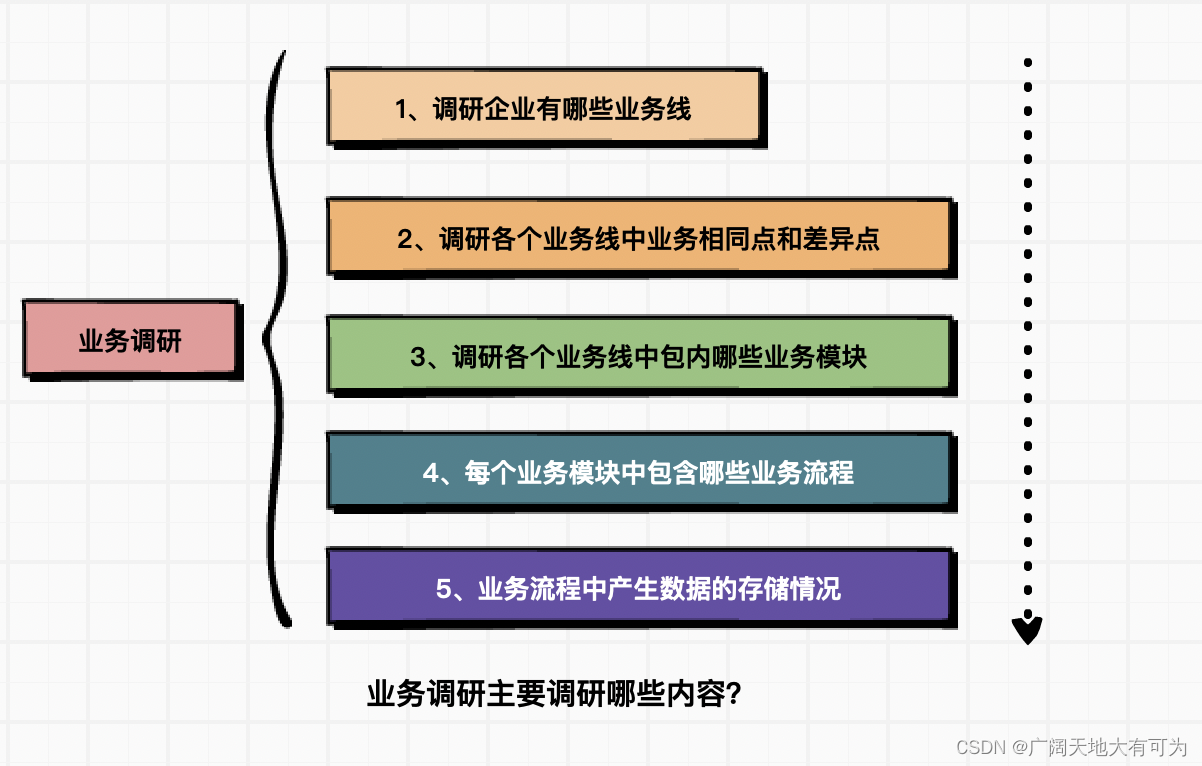
業務調研完后的產出：

? ? ? ? 業務調研表、各個業務流程圖

---

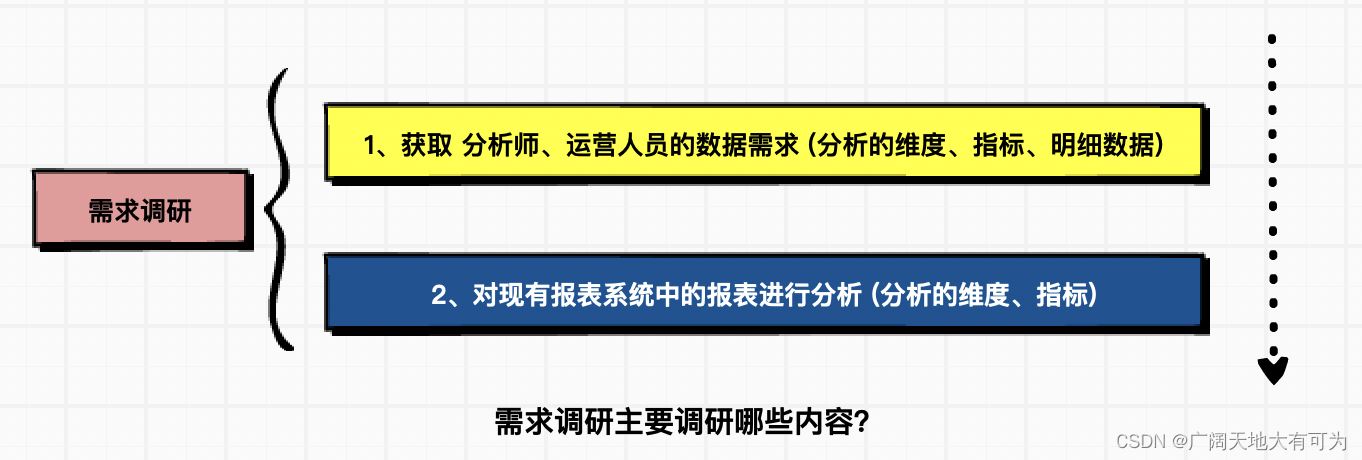
需求調研

? ? ? ? 主要調研 分析師、運營人員的數據需求 和 現有報表系統中的數據需求? ? ? ??

---

1.2 數倉架構設計

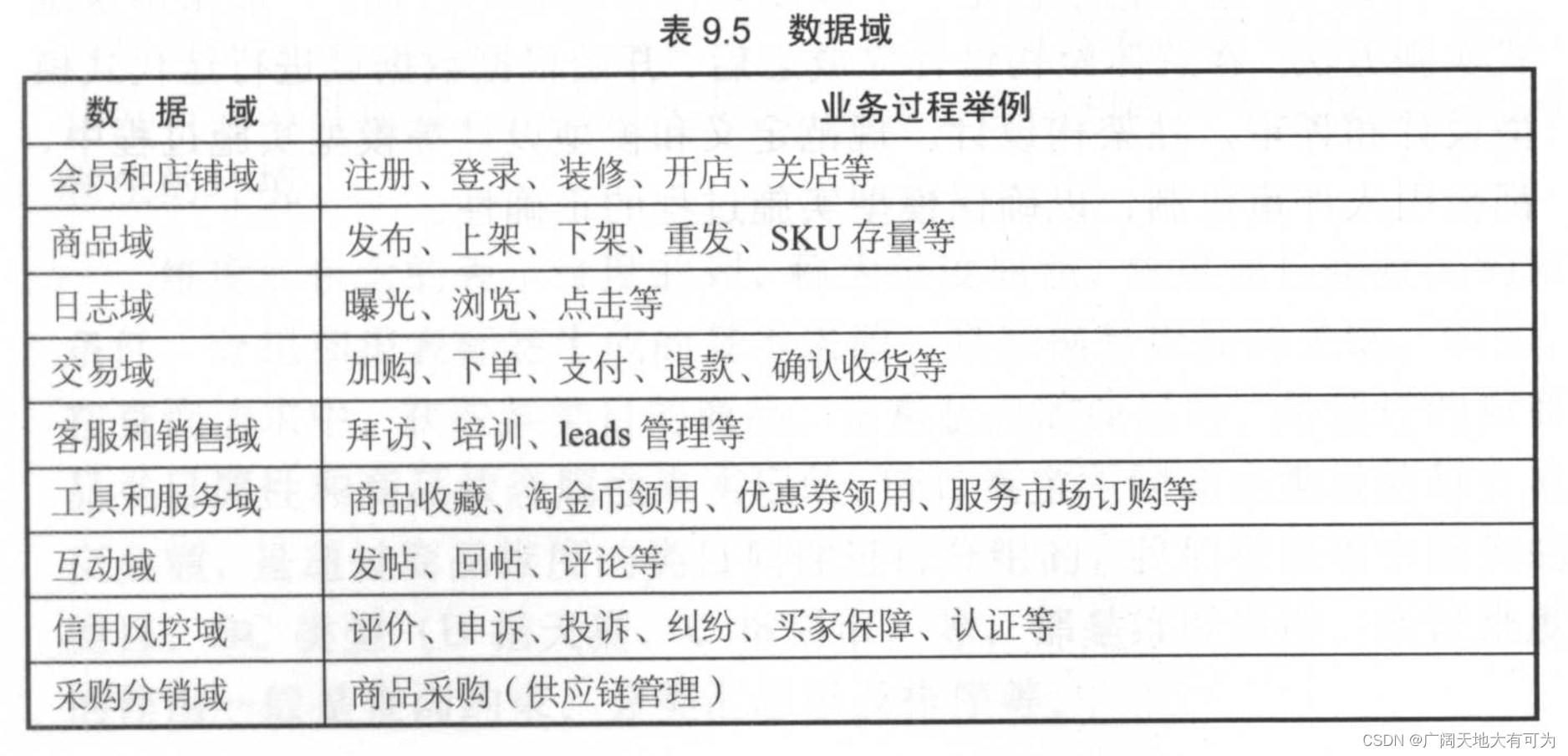
數據域(主題域)的劃分

? ? ? ? 進行數據調研后，需要對 業務過程或維度進行歸納、抽象出數據域

? ? ? ? 數據域的特點：

? ? ? ? ? ? ? ? 為保證數倉的穩定性，數據域需要從業務過程中抽象提煉

? ? ? ? ? ? ? ? 并且長期維護和更新，但不輕易變動

? ? ? ? ? ? ? ? 劃分數據域時，既要能覆蓋當前所有的業務需求，又要在有新的業務進入時

? ? ? ? ? ? ? ? 毫無影響的進入已有的數據域或者擴展新的數據域

---

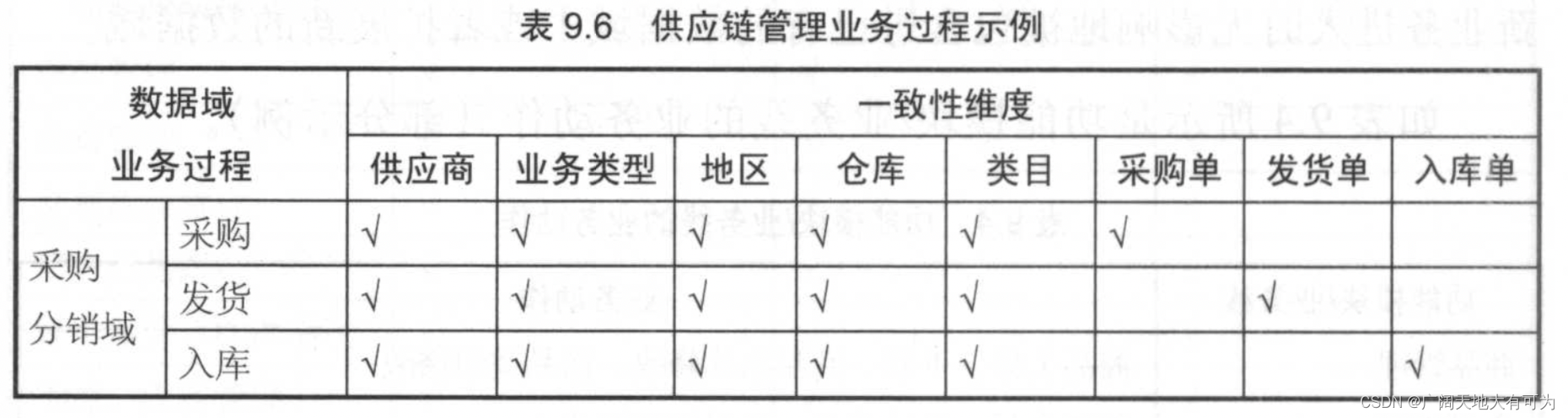
構建總線矩陣

? ? ? ? 構建總線矩陣的目的是為了明確兩個事情：

? ? ? ? ? ? ? ? 1、明確每個數據域下有哪些業務過程

? ? ? ? ? ? ? ? 2、明確每個業務過程與哪些維度相關

---

1.3 規范定義

? ? ? ? 規范定義主要包括：表命名規范、字段命名規范、ETL開發規范 (后續章節會單獨介紹這塊內容)

1.4 模型設計

? ? ? ? 模型設計主要包括：事實表設計、維度表設計 (后續章節會單獨介紹這塊內容)

1.5?代碼開發

? ? ? ? ETL開發過程

1.6 評審

? ? ? ? 對設計的模型、開發代碼進行評審

1.7?上線及配置質量監控

? ? ? ? 調度任務上線及配置質量監控任務

1.8?總結

? ? ? ? 數倉的建設是一個高度迭代和動態的過程，一般采用螺旋式實施方法。

? ? ? ? 在總體架構設計完成之后，開始根據數據域進行迭代式模型設計和評審

? ? ? ? 在架構設計、規范定義、模型設計等過程中，都要引入評審機制，以確保實施過程的正確性

????????