? ?
目錄
多元線性回歸模型
總體回歸函數
樣本回歸函數
線性回歸模型的假定
普通最小二乘法(Ordinary Least Squares,OLS)
擬合優度指標
F檢驗
回歸系數的t檢驗
Python中構建多元線性回歸模型
數據理解
數據讀取
數據清洗
相關分析
回歸分析
附錄
參考文獻
? ? ? ? 閱讀本文時,建議先閱讀《第7章-使用統計方法進行變量有效性測試-7.4.1-簡單線性回歸》。
多元線性回歸模型
總體回歸函數
? ? ? ? 多元線性回歸是在一元線性回歸的基礎之上,增加更多的自變量(兩個或兩個以上),其表達形式如下:
?其中是因變量,
是
個自變量。
是干擾項或隨機誤差項。
是回歸系數,特別的
是截距。
樣本回歸函數
? ? ? ? 和一元線性回歸類似,其表達形式如下:
其中是
個自變量,
是回歸系數的估計。
稱為樣本剩余項,或殘差。
? ? ? ? 假設現在樣本數據如下:
| 自變量 | 自變量 | ...... | 自變量 | 因變量 |
|---|---|---|---|---|
| ...... | ||||
| ...... | ||||
| ...... | ...... | ...... | ...... | ...... |
| ...... |
表格中每一行表示一個樣本,總共個樣本。對于第
個樣本
預測值如下:
對于上面n個樣本,可以使用如下矩陣形式表示。
真實值
預測值
自變量值
回歸系數
回歸系數估計量
殘差
干擾項
有了上面矩陣形式的約定后,容易得到
總體回歸函數變為
樣本回歸函數變為
線性回歸模型的假定
(1)線性于參數
? ? ? ? 即討論的模型是關于參數的線性函數:
(2)擾動項與自變量不相關,期望值為0
數學表述如下:
? ? ? ? 該假設提示我們,只要擾動項與自變量相關,就應該繼續從擾動項中分析出新的自變量納入模型中。
(3)擾動項之間相互獨立且服從方差相等的同一個正態分布
數學表述如下:
,
? ? ? ?
? ? ? ? 其中分別表示第
個體的干擾項。擾動項代表個體的差異性,如果其不獨立,則說明個體之間相互影響,并且仍舊有重要的信息蘊含在其中未被提取出來。
(4)自變量之間相互獨立
數學表述如下:
? ? ? ? 自變量之間如果不相互獨立,多元線性回歸就會出現多重共線性,會導致回歸系數的估計值不穩定。關于多重共線性,后面再說。
普通最小二乘法(Ordinary Least Squares,OLS)
? ? ? ? 普通最小二乘法就是找到,是的殘差平方和最小。也就是:
如果使用矩陣來表示,假設,則上式可以寫成如下矩陣形式:
后面為了表述方便,對于多元線性回歸,我們將采用向量或者矩陣的形式。如沒特別說明,向量均為列向量。現在殘差平方和就可以如下轉換了:
可以看到是一個常數,對常數進行轉置是不改變其大小的,于是
這里求殘差平方和最小值,就涉及矩陣微積分的知識。可以參見《機器學習之矩陣微積分及其性質》標量-向量求導性質(4)。現在將上式兩邊對求導。
上式兩邊轉置
當可逆時,得到:
可以看到上式右邊均和樣本數據有關,也就是說,給定樣本,我們就可以計算出回歸系數估計值了。因為預測值與自變量有如下關系:
將估計量代入,記得到預測值與真實值之間的關系:
如果令,即得到
?注意到只與自變量
有關。
擬合優度指標
? ? ? ? 首先,我們看一下,在多元線性回歸模型中,如下恒等式是否還成立:
其中,為總離差平方和,或者總平方和(Total Sum of Squares),如下計算:
?
為回歸平方和,或者解釋平方和(Explained Sum of Squares),如下計算:
?
為殘差平方和,或者剩余平方和(Residual Sum of Squares),如下計算:
?
下面來證明。還是采用矩陣的形式。先令。
(1)第一步:將寫成矩陣形式,如下:
將后三項展開成向量的形式,得到:
注意到
所以:
(2)第二步,將寫成矩陣形式,同理得到:
(3)第三步,將寫成矩陣形式
(4)根據前3步,要想證明,就是要證明:
即:
因為,代入上式左邊,得到
因為,替換上式第一項,得到
下面只需要證明中間項為即可。
因為,
則,
即
,兩邊轉置有
于是得到恒等式成立。
于是和一元線性回歸擬合優度指標類似,如下定義
? ? ? ? ?我們注意到(R-squared)中并未考慮自變量的個數。在實際問題中,當增加自變量的個數時,
就會增加,即隨著自變量的增多,
會越來越大,會顯得回歸模型精度很高,有較好的擬合效果。而實際上可能并非如此,有些自變量與因變量完全不相關,增加這些自變量,并不會提升擬合水平和預測精度。為避免這種現象,調整的
則會懲罰多余的自變量,避免模型過度擬合。調整后的
(Adj. R-squared)如下:
?其中
(1)n是用于擬合回歸模型的樣本數量,
(2)p為模型中的自變量的個數,
(3)i表示是否有截距,當有截距時為1,否則為0。
? ? ? ? 可以證明調整后的小于
,并且調整后
的值不會由于自變量個數的增加而越來越接近1。
F檢驗
原假設:
,
備擇假設:
不全為0,
參見《第7章-使用統計方法進行變量有效性測試-7.2.1-單因素方差分析》,關于,可以得到如下關于自由度的結論:
(1)總離差平方和自由度為
,其中n為全部觀察值的個數,
(2)回歸平方和自由度為
,其中
為自變量個數,
(3)殘差平方和自由度為
,
發現自由度滿足此恒等式:。
可以如下定義各平方和的平均值:
(1)平均離差平方和,
(2)平均回歸平方和,
(3)平均殘差平方和
構造F統計量
可以參見《第7章-使用統計方法進行變量有效性測試-7.2.1-單因素方差分析》,證明該統計服從如下F分布:
回歸系數的t檢驗
? ? ? ? 回歸系數的t檢驗是對每個回歸系數檢驗。如果對第i個回歸系數估計量進行檢驗,那么假設問題如下:
原假設
備擇假設
擾動項,
的估計為
。
構造如下統計量:
其中是向量
的第i個值,
,
為矩陣
的第i行j列元素,
。
對于每個,都服從自由度為n-k-1的t分布。關于細節證明可以仿照一元線性回歸中的證明思路,只不過這里需要改成矩陣形式,后面有時間我們再不上。
Python中構建多元線性回歸模型
數據理解
? ? ? ? LR_practice.xlsx文件中給出的是一份汽車貸款的相關數據。希望使用多元線性回歸模型分析用戶年齡、用戶年收入、用戶所住小區房屋均價、當地人均等因素與信用卡月均支出的關系。
? ? ? ? 這里信用卡月均支出是多元線性回歸的因變量,而用戶年齡、用戶年收入、用戶所住小區房屋均價、當地人均等因素是多元線性回歸的自變量。
? ? ? ? Excel中的部分數據如下:
?全部數據如下:
id Acc avg_exp gender Age Income Ownrent Selfempl dist_home_val dist_avg_income edad2 edu_class
19 1 1217.03 Male 40 16.03515 1 1 99.93 15.93278947 1600 研究生
5 1 1251.5 Male 32 15.8475 1 0 49.88 15.79631579 1024 大學
86 1 856.57 Male 41 11.47285 1 0 16.1 11.27563158 1681 研究生
50 1 1321.83 Male 28 13.40915 1 0 100.39 13.34647368 784 大學
67 1 816.03 Male 41 10.03015 0 1 119.76 10.33226316 1681 研究生
97 1 1151.15 Male 33 11.70575 1 0 38.9 11.52605263 1089 研究生
38 1 1233.77 Male 37 11.81885 1 0 61.05 12.49089474 1369 研究生
100 1 802.52 Male 46 9.3126 1 0 58.74 9.053263158 2116 大學
30 1 2167.77 Male 40 16.28885 1 0 157.9 17.05668421 1600 研究生
25 1 654.58 Male 43 8.2129 1 0 106.45 8.574631579 1849 大學
99 1 1102.2 Male 26 10.311 1 0 126.69 10.77052632 676 大學
57 1 2430.03 Male 34 16.90015 0 0 141.43 18.427 1156 研究生
40 1 1052.35 Male 28 9.81175 1 0 121.88 10.99605263 784 研究生
1 1 791.98 Female 38 8.3799 1 0 49.11 9.103052632 1444 中學
26 1 1672.2 Female 30 9.571 0 0 94.72 10.23736842 900 研究生
3 1 1342 Female 34 7.91 1 0 58.92 7.749473684 1156 研究生
17 1 883.72 Male 40 8.3686 1 0 114.02 9.268526316 1600 研究生
24 1 726.64 Male 36 7.4332 0 0 130.46 8.043894737 1296 大學
7 1 552.83 Female 28 6.62415 0 0 75.85 7.784368421 784 中學
11 1 987.66 Male 31 8.5383 1 0 33.47 9.129789474 961 中學
68 1 1214.54 Female 42 6.6727 0 0 79.92 6.448631579 1764 研究生
9 1 1472.82 Male 37 10.9641 1 0 94.07 12.20115789 1369 大學
77 1 744.66 Female 24 7.3733 0 0 22.72 8.424 576 中學
98 1 1344.05 Female 25 7.02025 0 0 136.05 7.090263158 625 研究生
36 1 1778.3 Female 43 9.1315 1 0 33.21 9.705789474 1849 研究生
39 1 834.47 Male 27 7.62235 0 0 41.38 8.689315789 729 研究生
73 1 648.15 Male 33 6.14075 0 0 28.49 6.992894737 1089 中學
10 1 884.58 Female 28 5.9229 0 0 51.89 6.946210526 784 大學
16 1 1606.43 Female 41 7.93215 1 0 86.11 8.761210526 1681 研究生
32 1 959.83 Male 29 7.79915 0 0 58.59 8.411210526 841 大學
58 1 1992.39 Female 33 9.84195 0 0 60.52 11.06257895 1089 研究生
33 0 Female 25 3.15 0 1 6.31 2.76 625 小學及以下
70 1 1752.47 Female 25 8.53235 0 0 85.08 9.339842105 625 研究生
79 1 1434.55 Female 36 6.92275 0 0 57.75 7.766578947 1296 研究生
61 1 565.8 Female 25 5.729 0 0 75.25 5.912631579 625 中學
41 1 1581.94 Female 26 7.6097 1 0 61.72 8.332315789 676 研究生
56 1 711.89 Female 33 6.45945 0 0 58.63 7.071526316 1089 中學
18 0 Female 30 3 0 1 106.8 3.7 900 中學
35 1 994.54 Female 24 6.2727 0 0 17.41 7.194947368 576 大學
78 1 888.46 Female 25 5.6223 0 0 71.7 6.046631579 625 大學
92 0 Female 999 2.81 0 1 119.98 2.56 2025
63 1 701.07 Female 26 6.20535 0 0 123.52 6.694578947 676 中學
54 1 806.13 Female 24 5.13065 0 0 112.93 5.863315789 576 大學
74 1 1299.37 Female 37 5.91685 0 0 118.77 5.975105263 1369 研究生
64 1 809.51 Female 22 5.04755 0 0 98.92 5.801105263 484 大學
82 1 610.25 Female 55 3.99125 1 0 116.93 4.932368421 3025 大學
45 0 Female 38 2.6 0 0 29.83 3.11 1444 小學及以下
42 1 485.65 Female 23 4.91825 0 0 50.15 5.470789474 529 中學
80 1 963.68 Female 33 5.6684 0 0 100.92 6.192526316 1089 大學
4 1 993.87 Female 31 5.80935 0 0 66.71 6.111421053 961 大學
29 0 Female 34 2.5 0 1 25.59 2.48 1156 小學及以下
6 1 524 Female 23 5.02 0 0 14.76 5.252631579 529 中學
34 1 1403.72 Female 21 7.7886 1 0 133.18 7.948526316 441 大學
71 1 1629.05 Female 31 7.30525 1 0 64.61 8.310263158 961 研究生
14 1 745.87 Female 29 6.07935 1 0 96.51 7.020368421 841 中學
2 0 Female 33 2.42 0 0 40.57 3.43 1089 中學
55 1 527.19 Female 26 4.93595 0 0 24.95 5.759421053 676 中學
93 1 520.38 Female 43 4.9019 0 0 13.13 5.253578947 1849 中學
84 1 251.56 Female 29 5.1578 0 0 63.23 5.492947368 841 小學及以下
8 1 817.79 Female 29 6.35895 1 0 44.39 6.318894737 841 中學
49 1 889.08 Female 26 5.0954 0 0 50.88 5.909894737 676 大學
21 1 1048.34 Female 35 5.8917 1 0 67.47 7.078105263 1225 大學
62 1 847.78 Female 27 4.8189 0 0 57.69 5.952526316 729 大學
75 1 593.11 Female 27 5.06555 0 0 38.06 5.556368421 729 中學
31 1 772.69 Female 22 4.19345 0 0 62.29 5.237315789 484 大學
52 1 545.2 Female 24 4.626 0 0 119.39 4.454210526 576 中學
23 1 905.52 Female 34 6.4276 1 0 27.82 6.960631579 1156 中學
47 1 1175.49 Female 36 6.17745 0 0 109.06 7.327315789 1296 大學
72 1 1006.35 Female 27 5.33175 0 0 133.26 6.557105263 729 大學
15 1 727.62 Female 35 5.4481 1 0 32.98 5.924315789 1225 中學
44 1 695.85 Female 30 5.22925 0 0 73.69 5.967105263 900 中學
53 1 491.04 Female 21 4.0552 0 0 36.81 4.349157895 441 中學
83 1 468.61 Female 20 3.89305 0 0 66.75 4.551105263 400 中學
43 1 593.92 Female 30 4.3796 0 0 124.23 5.040631579 900 中學
60 1 418.78 Female 21 3.4939 0 0 34.46 3.828842105 441 中學
28 1 163.18 Female 22 3.8159 0 0 63.27 3.997789474 484 小學及以下數據字典如下:
| 字段名稱 | 中文含義 |
| id | 編號 |
| Acc | 是否開卡(1=已開通) |
| avg_exp | 月均信用卡支出(元) |
| gender | 性別 |
| Age | 年齡 |
| Income | 年收入(萬元) |
| Ownrent | 是否自有住房(有=1;無=0) |
| Selfempl | 是否自謀職業(1=yes, 0=no) |
| dist_home_val | 所住小區房屋均價(萬元) |
| dist_avg_income | 當地人均收入 |
| edad2 | |
| edu_class | 教育等級:小學及以下,中學,本科,研究生 |
其中edad2是設置的一項無關數據(以便后面描述清洗使用)。
數據讀取
? ? ? ? 可以使用代碼方式讀取數據,并查詢數據集的基本信息,為后續數據清洗做準備。代碼如下:
import pandas as pd
from statsmodels.formula.api import ols
import matplotlib.pyplot as plt
from scipy import statsif __name__ == '__main__':# 讀取信用卡消費數據data_path = r'E:\證書認證\CDA\Level2code&data\第7章-假設檢驗與方差分析、線性回歸、邏輯回歸\線性回歸\LR_practice.xlsx'data_raw_df = pd.read_excel(data_path)print('原始數據data_raw_df=', '\n', data_raw_df)print('-----------------------------------------------------------------')# 打印原始數據信息print('原始數據信息data_raw_info=')data_raw_df.info()print('-----------------------------------------------------------------')運行結果,如下:
原始數據data_raw_df= id Acc avg_exp gender ... dist_home_val dist_avg_income edad2 edu_class
0 19 1 1217.03 Male ... 99.93 15.932789 1600 研究生
1 5 1 1251.50 Male ... 49.88 15.796316 1024 大學
2 86 1 856.57 Male ... 16.10 11.275632 1681 研究生
3 50 1 1321.83 Male ... 100.39 13.346474 784 大學
4 67 1 816.03 Male ... 119.76 10.332263 1681 研究生
.. .. ... ... ... ... ... ... ... ...
71 53 1 491.04 Female ... 36.81 4.349158 441 中學
72 83 1 468.61 Female ... 66.75 4.551105 400 中學
73 43 1 593.92 Female ... 124.23 5.040632 900 中學
74 60 1 418.78 Female ... 34.46 3.828842 441 中學
75 28 1 163.18 Female ... 63.27 3.997789 484 小學及以下[76 rows x 12 columns]
-----------------------------------------------------------------
原始數據信息data_raw_info=
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 76 entries, 0 to 75
Data columns (total 12 columns):# Column Non-Null Count Dtype
--- ------ -------------- ----- 0 id 76 non-null int64 1 Acc 76 non-null int64 2 avg_exp 70 non-null float643 gender 76 non-null object 4 Age 76 non-null int64 5 Income 76 non-null float646 Ownrent 76 non-null int64 7 Selfempl 76 non-null int64 8 dist_home_val 76 non-null float649 dist_avg_income 76 non-null float6410 edad2 76 non-null int64 11 edu_class 75 non-null object
dtypes: float64(4), int64(6), object(2)
memory usage: 7.2+ KB
-----------------------------------------------------------------? ? ? ? 從打印的數據來看,總計有76行數據,共有12個列。從數據集的基本信息,顯示了數據的字段編號,字段名稱,非空個數統計,數據類型。非空個數統計表明如下兩個字段存在空值。
2 avg_exp 70 non-null float64
11 edu_class 75 non-null object 數據清洗
? ? ? ? 根據數據讀取,初步分析的情況,指定如下清洗策略:
(1)刪除無關的列
? ? ? ? 有些列的數據是無實質性意義的,或者和分析無關。比如id,edad2。而Acc字段表示用戶是否開卡,只有開卡用戶才會有信用卡支出,因此Acc不能進入模型,也需要刪除。
(2)刪除重復數據
? ? ? ? 在這份數據中,重復數據可以看成是臟數據,直接刪除。
(3)缺失值填充
? ? ? ? 可以通過代碼查看數據缺失情況,然后針對每種情況,使用不同的缺失值填充策略,完成缺失值填充。
(4)數據轉換
? ? ? ? 有些數據可能是文本型的數據,不能直接用于數據分析。需要將其轉換成數值型數據,例如gender取值為Male,Female,需要將其轉換成數值型,比如Male轉換成1,Female轉換成0。
(5)異常值處理
? ? ? ? 有些數據明顯是異常數據,影響整體的分析效果,需要將其刪除,或者使用正常值填充。這里可以使用原則。本文實現的時候,也是使用的該原則。
(6)對多分類自變量進行啞變量變換
? ? ? ??對于多分類自變量,假如直接將其納入分析模型,得出的結果就會不精確,甚至會得到錯誤的結論。這是因為多分類自變量直接當作定量數據來計算,人為的拔高了數據的“維度”和豐富程度,此時,我們應當多分類自變量進行啞變量處理。
? ? ? ? 啞變量(Dummy Variable)是一種用來表示分類變量的方法,它將每個類別轉化為一個二進制變量(0和1表示)。基本原理是將有k個類別的多分類自變量轉換為k個啞變量(二進制變量)。在實際分析中,一般取一個類別作為參照水平,而將剩下的k-1個啞變量納入模型。例如本例中有教育程度edu_class,是一個多分類自變量。總共有4個類別,轉換成數值型后為0,1,2,3。其中有一些數據edu_class空白,使用其他類別來填充,比如4。現在得到edu_class的類別為0,1,2,3,4。假設上面76行數據中,edu_class這一列數據如下:
| edu_class |
| 0 |
| 1 |
| 1 |
| ... |
| 2 |
| 4 |
進行啞變量變換后,后面增加5列,每一列代表一個啞變量。如下:
| edu_class | dummy_0 | dummy_1 | dummy_2 | dummy_3 | dummy_4 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| ... | ... | ... | ... | ... | ... |
| 2 | 0 | 0 | 1 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 1 |
比如第一行,edu_class類別為0,那么后面增加的5列,dummy_0為1,其余為0。下面使用代碼實現上述清洗策略,如下:
import pandas as pd
from statsmodels.formula.api import ols
import matplotlib.pyplot as plt
from scipy import statsif __name__ == '__main__':# 讀取信用卡消費數據data_path = r'E:\證書認證\CDA\Level2code&data\第7章-假設檢驗與方差分析、線性回歸、邏輯回歸\線性回歸\LR_practice.xlsx'data_raw_df = pd.read_excel(data_path)print('原始數據data_raw_df=', '\n', data_raw_df)print('-----------------------------------------------------------------')# 打印原始數據信息print('原始數據信息data_raw_info=')data_raw_df.info()print('-----------------------------------------------------------------')# 刪除無用字段# inplace=True表示直接在原始數據上刪除列,返回None,inplace=False表示復制一份然后刪除列,返回刪除后的數據# axis=1或者columns表示刪除按列名刪除列,axis=0或者index表示按照索引刪除行.data_drop_col_df = data_raw_df.drop(['id', 'Acc', 'edad2'], axis='columns', inplace=False)print('刪除無用的列后data_drop_col_df=', '\n', data_drop_col_df)print('-----------------------------------------------------------------')# 刪除重復數據df = data_drop_col_df.drop_duplicates()print('刪除重復數據df=', '\n', df)print('-----------------------------------------------------------------')# 缺失值填補 avg_exp 和 edu_class 存在缺失值.data_isnull_mean = df.isnull().mean()print('數據缺失情況data_isnull_mean=', '\n', data_isnull_mean)# 使用平均值填補avg_exp缺失值avg_exp_col = 'avg_exp'df[avg_exp_col] = df[avg_exp_col].fillna(df[avg_exp_col].mean())# 填補edu_classedu_class_col = 'edu_class'edu_class_label = df[edu_class_col].unique().tolist() # 獲取教育水平的類別,缺失值顯示為nan.print('教育水平類別edu_class_label=', '\n', edu_class_label)df[edu_class_col] = df[edu_class_col].apply(lambda x: edu_class_label.index(x)) # 將教育水平轉換成數字索引.# 性別gender數據轉換gender_col = 'gender'df[gender_col] = df[gender_col].map({'Male': 1, 'Female': 0})print('df=', '\n', df)# 打印缺失值填補后的數據print('缺失值填補后的數據信息如下:')df.info()print('-----------------------------------------------------------------')# 異常值處理age_col = 'Age'zscore = stats.zscore(df[age_col])print('年齡zscore=', '\n', zscore)my_zscore = (df - df[age_col].mean()) / df[age_col].std() # (每個值-平均值)/標準差print('自己實現的my_zscore=', '\n', zscore)z_outlier = (zscore > 3) | (zscore < -3) # 這里使用了3-sigma原則,|xi-u|>3sigma的數據是異常數據.print('z_outlier=', '\n', z_outlier)except_index = z_outlier.tolist().index(1) # 異常數據的位置索引.print('異常數據索引位置except_index=', except_index)# 異常值填充:排除異常值后,計算均值進行填充.df_mean = df[age_col].drop(except_index, inplace=False)df[age_col].iloc[except_index] = df_mean.mean()print('-----------------------------------------------------------------')# 啞變量dummy = pd.get_dummies(df[edu_class_col], prefix='edu').iloc[:, 1:]print('啞變量dummy=', '\n', dummy)data = pd.concat([df, dummy], axis=1)print('拼接啞變量data=', '\n', data)print('-----------------------------------------------------------------')運行結果如下:
刪除無用的列后data_drop_col_df= avg_exp gender Age ... dist_home_val dist_avg_income edu_class
0 1217.03 Male 40 ... 99.93 15.932789 研究生
1 1251.50 Male 32 ... 49.88 15.796316 大學
2 856.57 Male 41 ... 16.10 11.275632 研究生
3 1321.83 Male 28 ... 100.39 13.346474 大學
4 816.03 Male 41 ... 119.76 10.332263 研究生
.. ... ... ... ... ... ... ...
71 491.04 Female 21 ... 36.81 4.349158 中學
72 468.61 Female 20 ... 66.75 4.551105 中學
73 593.92 Female 30 ... 124.23 5.040632 中學
74 418.78 Female 21 ... 34.46 3.828842 中學
75 163.18 Female 22 ... 63.27 3.997789 小學及以下[76 rows x 9 columns]
-----------------------------------------------------------------
刪除重復數據df= avg_exp gender Age ... dist_home_val dist_avg_income edu_class
0 1217.03 Male 40 ... 99.93 15.932789 研究生
1 1251.50 Male 32 ... 49.88 15.796316 大學
2 856.57 Male 41 ... 16.10 11.275632 研究生
3 1321.83 Male 28 ... 100.39 13.346474 大學
4 816.03 Male 41 ... 119.76 10.332263 研究生
.. ... ... ... ... ... ... ...
71 491.04 Female 21 ... 36.81 4.349158 中學
72 468.61 Female 20 ... 66.75 4.551105 中學
73 593.92 Female 30 ... 124.23 5.040632 中學
74 418.78 Female 21 ... 34.46 3.828842 中學
75 163.18 Female 22 ... 63.27 3.997789 小學及以下[76 rows x 9 columns]
-----------------------------------------------------------------
數據缺失情況data_isnull_mean= avg_exp 0.078947
gender 0.000000
Age 0.000000
Income 0.000000
Ownrent 0.000000
Selfempl 0.000000
dist_home_val 0.000000
dist_avg_income 0.000000
edu_class 0.013158
dtype: float64
教育水平類別edu_class_label= ['研究生', '大學', '中學', '小學及以下', nan]
df= avg_exp gender Age ... dist_home_val dist_avg_income edu_class
0 1217.03 1 40 ... 99.93 15.932789 0
1 1251.50 1 32 ... 49.88 15.796316 1
2 856.57 1 41 ... 16.10 11.275632 0
3 1321.83 1 28 ... 100.39 13.346474 1
4 816.03 1 41 ... 119.76 10.332263 0
.. ... ... ... ... ... ... ...
71 491.04 0 21 ... 36.81 4.349158 2
72 468.61 0 20 ... 66.75 4.551105 2
73 593.92 0 30 ... 124.23 5.040632 2
74 418.78 0 21 ... 34.46 3.828842 2
75 163.18 0 22 ... 63.27 3.997789 3[76 rows x 9 columns]
缺失值填補后的數據信息如下:
<class 'pandas.core.frame.DataFrame'>
Int64Index: 76 entries, 0 to 75
Data columns (total 9 columns):# Column Non-Null Count Dtype
--- ------ -------------- ----- 0 avg_exp 76 non-null float641 gender 76 non-null int64 2 Age 76 non-null int64 3 Income 76 non-null float644 Ownrent 76 non-null int64 5 Selfempl 76 non-null int64 6 dist_home_val 76 non-null float647 dist_avg_income 76 non-null float648 edu_class 76 non-null int64
dtypes: float64(4), int64(5)
memory usage: 5.9 KB
-----------------------------------------------------------------
年齡zscore= 0 -0.035723
1 -0.108122
2 -0.026673
3 -0.144321
4 -0.026673...
71 -0.207670
72 -0.216720
73 -0.126221
74 -0.207670
75 -0.198620
Name: Age, Length: 76, dtype: float64
自己實現的my_zscore= 0 -0.035723
1 -0.108122
2 -0.026673
3 -0.144321
4 -0.026673...
71 -0.207670
72 -0.216720
73 -0.126221
74 -0.207670
75 -0.198620
Name: Age, Length: 76, dtype: float64
z_outlier= 0 False
1 False
2 False
3 False
4 False...
71 False
72 False
73 False
74 False
75 False
Name: Age, Length: 76, dtype: bool
異常數據索引位置except_index= 40
-----------------------------------------------------------------
啞變量dummy= edu_1 edu_2 edu_3 edu_4
0 0 0 0 0
1 1 0 0 0
2 0 0 0 0
3 1 0 0 0
4 0 0 0 0
.. ... ... ... ...
71 0 1 0 0
72 0 1 0 0
73 0 1 0 0
74 0 1 0 0
75 0 0 1 0[76 rows x 4 columns]
拼接啞變量data= avg_exp gender Age Income ... edu_1 edu_2 edu_3 edu_4
0 1217.03 1 40.0 16.03515 ... 0 0 0 0
1 1251.50 1 32.0 15.84750 ... 1 0 0 0
2 856.57 1 41.0 11.47285 ... 0 0 0 0
3 1321.83 1 28.0 13.40915 ... 1 0 0 0
4 816.03 1 41.0 10.03015 ... 0 0 0 0
.. ... ... ... ... ... ... ... ... ...
71 491.04 0 21.0 4.05520 ... 0 1 0 0
72 468.61 0 20.0 3.89305 ... 0 1 0 0
73 593.92 0 30.0 4.37960 ... 0 1 0 0
74 418.78 0 21.0 3.49390 ... 0 1 0 0
75 163.18 0 22.0 3.81590 ... 0 0 1 0[76 rows x 13 columns]相關分析
? ? ? ? 之前我們說過,相關分析是回歸分析的基礎。如果自變量和因變量毫不相關,進一步回歸分析也沒有意義。下面計算各變量之間的相關系數。
# 之前我們說相關分析是回歸分析的基礎。在建立回歸分析模型前先,需要做自變量和因變量之間的相關分析.# 月均信用卡支出(元)、性別(男=1,女=0)、是否有自住房(有=1,無=0)、是否自謀職業(是=1,否=0)、教育等級corr_col = ['avg_exp', 'gender', 'Ownrent', 'Selfempl', 'edu_class', 'Income']cor_relation = data[corr_col].corr(method='kendall') # 肯德爾等級相關系數print('相關系數cor_relation=', '\n', cor_relation)print('-----------------------------------------------------------------')運行結果如下:
相關系數cor_relation= avg_exp gender Ownrent Selfempl edu_class Income
avg_exp 1.000000 0.167236 0.290705 0.064150 -0.561243 0.421110
gender 0.167236 1.000000 0.430469 0.046657 -0.351901 0.558598
Ownrent 0.290705 0.430469 1.000000 -0.115370 -0.300133 0.474305
Selfempl 0.064150 0.046657 -0.115370 1.000000 0.154962 -0.135274
edu_class -0.561243 -0.351901 -0.300133 0.154962 1.000000 -0.551915
Income 0.421110 0.558598 0.474305 -0.135274 -0.551915 1.000000
-----------------------------------------------------------------從結果來看,與avg_exp相關性最高的是edu_class,為-0.561243(忽略正負)。從整體來看,各個自變量之間都有一定的相關性,但是相關性不是很高。雖然違背了多元線性模型的假定,但相關性不至于影響到回歸模型不能使用。
? ? ? ? 除了使用相關系數來分析各變量之間的相關程度,也可以使用可視化的方式顯示各變量的分布情況,例如散點圖。下面看下,avg_exp和Income之間的關系,代碼如下:
# 繪制散點圖plt.rcParams["font.sans-serif"] = ["SimHei"] # 顯示中文plt.scatter(data['Income'], data['avg_exp'])plt.xlabel('Income-年收入(萬元)')plt.ylabel('avg_exp-月均信用卡支出(元)')plt.title('年收入與月均信用卡支出散點圖')plt.show()print('-----------------------------------------------------------------')運行結果如下:
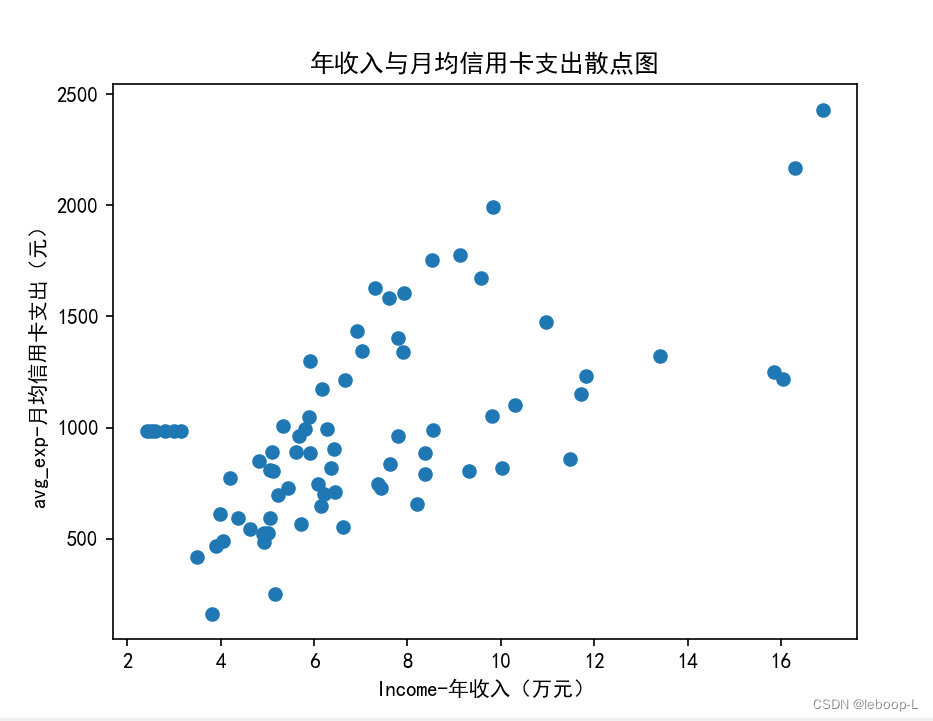
??從圖中可以看到,Income與avg_exp存在一定的正相關性。
回歸分析
? ? ? ? 經過上面的數據清洗,相關分析,可以進入正式主題了。這里使用statsmodels模塊的ols構建多元線性回歸模型。代碼如下:
# 建立多元線性模型formula = 'avg_exp~gender+Age+Income+Ownrent+Selfempl+dist_home_val+dist_avg_income+edu_1+edu_2+edu_3+edu_4'model = ols(formula=formula, data=data) # 建立模型model = model.fit() # 訓練summary = model.summary()print('summary=', '\n', summary)?第一步:定義formula,因變量與自變量之間使用~連接,因變量寫在左邊,多個自變量之間使用加號+連接。
第二步:定義模型,傳入公式和數據。
第三步:使用數據擬合模型,也就是fit()方法。
第四步:模型擬合優度等summary信息查看,主要看下擬合效果如何。
運行結果,如下:
summary= OLS Regression Results
==============================================================================
Dep. Variable: avg_exp R-squared: 0.720
Model: OLS Adj. R-squared: 0.671
Method: Least Squares F-statistic: 14.93
Date: Thu, 23 Nov 2023 Prob (F-statistic): 8.36e-14
Time: 14:07:25 Log-Likelihood: -519.52
No. Observations: 76 AIC: 1063.
Df Residuals: 64 BIC: 1091.
Df Model: 11
Covariance Type: nonrobust
===================================================================================coef std err t P>|t| [0.025 0.975]
-----------------------------------------------------------------------------------
Intercept 535.9565 223.038 2.403 0.019 90.387 981.526
gender -447.4828 97.100 -4.608 0.000 -641.463 -253.503
Age 0.6121 4.779 0.128 0.898 -8.936 10.160
Income -119.1929 72.411 -1.646 0.105 -263.850 25.464
Ownrent 41.3184 76.416 0.541 0.591 -111.341 193.977
Selfempl 153.7000 129.424 1.188 0.239 -104.853 412.253
dist_home_val 0.1579 0.859 0.184 0.855 -1.557 1.873
dist_avg_income 211.5250 71.122 2.974 0.004 69.442 353.608
edu_1 -262.5083 82.890 -3.167 0.002 -428.100 -96.916
edu_2 -495.1400 92.266 -5.366 0.000 -679.462 -310.818
edu_3 -292.5211 156.617 -1.868 0.066 -605.400 20.358
edu_4 49.3783 294.618 0.168 0.867 -539.188 637.945
==============================================================================
Omnibus: 0.894 Durbin-Watson: 2.112
Prob(Omnibus): 0.640 Jarque-Bera (JB): 0.613
Skew: -0.219 Prob(JB): 0.736
Kurtosis: 3.044 Cond. No. 1.00e+03
==============================================================================Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 1e+03. This might indicate that there are
strong multicollinearity or other numerical problems.Process finished with exit code 0
考慮到模型的總結結果比較重要。這里做一些詳細解釋和分析。上面的結果分為兩部分
第一步結果如下:
| Dep. Variable: ? ? ? ? ? ? ? ?avg_exp | 因變量:avg_exp |
| Model: ? ? ? ? ? ? ? ? ? ? ? ? ? ?OLS | 模型名稱:OLS |
| Method: ? ? ? ? ? ? ? ? Least Squares | 模型方法:最小二乘法 |
| Date: ? ? ? ? ? ? ? ?Thu, 23 Nov 2023 | 模型日期信息 |
| Time: ? ? ? ? ? ? ? ? ? ? ? ?14:21:52 | 模型時間信息 |
| No. Observations: ? ? ? ? ? ? ? ? ?76 | 觀測值數量:n=76 |
| Df Residuals: ? ? ? ? ? ? ? ? ? ? ?64 | 殘差自由度n-k-1=76-11-1=64 |
| Df Model: ? ? ? ? ? ? ? ? ? ? ? ? ?11 | 自變量個數k=11,對應代碼中formula自變量個數 |
| Covariance Type: ? ? ? ? ? ?nonrobust | |
| R-squared: ? ? ? ? ? ? ? ? ? ? ? 0.720 |
|
| Adj. R-squared: ? ? ? ? ? ? ? ? ?0.671 | 調整后的 |
| F-statistic: ? ? ? ? ? ? ? ? ? ? 14.93 | F統計值 |
| Prob (F-statistic): ? ? ? ? ? 8.36e-14 | p-值,大于F統計值的概率 |
| Log-Likelihood: ? ? ? ? ? ? ? ?-519.52 | 對數最大似然 |
| AIC: ? ? ? ? ? ? ? ? ? ? ? ? ? ? 1063. | AIC準則,評估回歸模型優劣的指標 |
| BIC: ? ? ? ? ? ? ? ? ? ? ? ? ? ? 1091. | BIC準則,評估回歸模型優劣的指標 |
其中Log-Likelihood,AIC,BIC這三個本文未涉及,后續涉及再細說。
第二部分結果詳細給出了樣本回歸函數,以及回歸系數估計量的t檢驗信息。
===================================================================================coef std err t P>|t| [0.025 0.975]
-----------------------------------------------------------------------------------
Intercept 535.9565 223.038 2.403 0.019 90.387 981.526
gender -447.4828 97.100 -4.608 0.000 -641.463 -253.503
Age 0.6121 4.779 0.128 0.898 -8.936 10.160
Income -119.1929 72.411 -1.646 0.105 -263.850 25.464
Ownrent 41.3184 76.416 0.541 0.591 -111.341 193.977
Selfempl 153.7000 129.424 1.188 0.239 -104.853 412.253
dist_home_val 0.1579 0.859 0.184 0.855 -1.557 1.873
dist_avg_income 211.5250 71.122 2.974 0.004 69.442 353.608
edu_1 -262.5083 82.890 -3.167 0.002 -428.100 -96.916
edu_2 -495.1400 92.266 -5.366 0.000 -679.462 -310.818
edu_3 -292.5211 156.617 -1.868 0.066 -605.400 20.358
edu_4 49.3783 294.618 0.168 0.867 -539.188 637.945
==============================================================================?coef列表示樣本回歸函數的回歸系數。其中第一個系數Intercept表示截距,也就是
的值。第3列t表示每個回歸系數
對應的t統計量
。P>|t|表示p-值,最后兩列放在一起表示置信區間。關于置信區間這里暫時不展開討論。
模型解釋
? ? ? ? 從以上結果中,可以看到模型的為0.720,擬合效果還是不錯的。默認顯著性水平
,F檢驗的p值為8.36e-14,接近0,拒絕原假設
:
,說明回歸系數不為0。從單個系數的顯著性t檢驗來看,初步判斷gender、dist_avg_income及edu_class是顯著的,P>|t|的值接近0。對于目前表現不顯著的變量,需要進一步對模型調優后作出顯著與否的判斷。
附錄
? ? ? ? 本文涉及的所有代碼如下:
import pandas as pd
from statsmodels.formula.api import ols
import matplotlib.pyplot as plt
from scipy import statsif __name__ == '__main__':# 讀取信用卡消費數據data_path = r'E:\證書認證\CDA\Level2code&data\第7章-假設檢驗與方差分析、線性回歸、邏輯回歸\線性回歸\LR_practice.xlsx'data_raw_df = pd.read_excel(data_path)print('原始數據data_raw_df=', '\n', data_raw_df)print('-----------------------------------------------------------------')# 打印原始數據信息print('原始數據信息data_raw_info=')data_raw_df.info()print('-----------------------------------------------------------------')# 刪除無用字段# inplace=True表示直接在原始數據上刪除列,返回None,inplace=False表示復制一份然后刪除列,返回刪除后的數據# axis=1或者columns表示刪除按列名刪除列,axis=0或者index表示按照索引刪除行.data_drop_col_df = data_raw_df.drop(['id', 'Acc', 'edad2'], axis='columns', inplace=False)print('刪除無用的列后data_drop_col_df=', '\n', data_drop_col_df)print('-----------------------------------------------------------------')# 刪除重復數據df = data_drop_col_df.drop_duplicates()print('刪除重復數據df=', '\n', df)print('-----------------------------------------------------------------')# 缺失值填補 avg_exp 和 edu_class 存在缺失值.data_isnull_mean = df.isnull().mean()print('數據缺失情況data_isnull_mean=', '\n', data_isnull_mean)# 使用平均值填補avg_exp缺失值avg_exp_col = 'avg_exp'df[avg_exp_col] = df[avg_exp_col].fillna(df[avg_exp_col].mean())# 填補edu_classedu_class_col = 'edu_class'edu_class_label = df[edu_class_col].unique().tolist() # 獲取教育水平的類別,缺失值顯示為nan.print('教育水平類別edu_class_label=', '\n', edu_class_label)df[edu_class_col] = df[edu_class_col].apply(lambda x: edu_class_label.index(x)) # 將教育水平轉換成數字索引.# 性別gender數據轉換gender_col = 'gender'df[gender_col] = df[gender_col].map({'Male': 1, 'Female': 0})print('df=', '\n', df)# 打印缺失值填補后的數據print('缺失值填補后的數據信息如下:')df.info()print('-----------------------------------------------------------------')# 異常值處理age_col = 'Age'zscore = stats.zscore(df[age_col])print('年齡zscore=', '\n', zscore)my_zscore = (df - df[age_col].mean()) / df[age_col].std() # (每個值-平均值)/標準差print('自己實現的my_zscore=', '\n', zscore)z_outlier = (zscore > 3) | (zscore < -3) # 這里使用了3-sigma原則,|xi-u|>3sigma的數據是異常數據.print('z_outlier=', '\n', z_outlier)except_index = z_outlier.tolist().index(1) # 異常數據的位置索引.print('異常數據索引位置except_index=', except_index)# 異常值填充:排除異常值后,計算均值進行填充.df_mean = df[age_col].drop(except_index, inplace=False)df[age_col].iloc[except_index] = df_mean.mean()print('-----------------------------------------------------------------')# 啞變量dummy = pd.get_dummies(df[edu_class_col], prefix='edu').iloc[:, 1:]print('啞變量dummy=', '\n', dummy)data = pd.concat([df, dummy], axis=1)print('拼接啞變量data=', '\n', data)print('-----------------------------------------------------------------')# 之前我們說相關分析是回歸分析的基礎。在建立回歸分析模型前先,需要做自變量和因變量之間的相關分析.# 月均信用卡支出(元)、性別(男=1,女=0)、是否有自住房(有=1,無=0)、是否自謀職業(是=1,否=0)、教育等級corr_col = ['avg_exp', 'gender', 'Ownrent', 'Selfempl', 'edu_class', 'Income']cor_relation = data[corr_col].corr(method='kendall') # 肯德爾等級相關系數print('相關系數cor_relation=', '\n', cor_relation)print('-----------------------------------------------------------------')# 繪制散點圖plt.rcParams["font.sans-serif"] = ["SimHei"] # 顯示中文plt.scatter(data['Income'], data['avg_exp'])plt.xlabel('Income-年收入(萬元)')plt.ylabel('avg_exp-月均信用卡支出(元)')plt.title('年收入與月均信用卡支出散點圖')plt.show()print('-----------------------------------------------------------------')# 建立多元線性模型formula = 'avg_exp ~ gender+Age+Income+Ownrent+Selfempl+dist_home_val+dist_avg_income+edu_1+edu_2+edu_3+edu_4'model = ols(formula=formula, data=data) # 建立模型model = model.fit() # 訓練summary = model.summary()print('summary=', '\n', summary)
參考文獻
https://home.ustc.edu.cn/~wdyknight/notes/reg_chap3.pdf




 97. 交錯字符串(動態規劃))

)
:Python Imaging Library(PIL)庫:圖像讀取、寫入、復制、粘貼、幾何變換、圖像增強、圖像濾波)










)
