方法一
給定一個含n(n>=1)個整數的數組,請設計一個在時間上盡可能高效的算法,找出數組中未出現的最小正整數。例如,數組{-5,3,2,3}中未出現的最小正整數是1;數組{1,2,3}中未出現的最小正整數是4。要求:
-
給出算法的基本設計思想。
-
根據設計思想,采用C或C++語言描述算法,關鍵之 處給出注釋。
-
說明你所設計算法的時間復雜度和空間復雜度。
讀完題目先找關鍵詞,這里可以直接提取這樣幾個關鍵詞
- 使用數組,求未出現的最小正整數
- 看到數組,是不是想到是否有序
- 時間+空間盡可能高效
暴力解:快速排序,然后掃描一遍數組
先對數組A快速排序得到升序序列,然后遍歷數組找到第一個未出現的最小正整數。
void Qsort(int A[], L, R){ //a數組保存數據,L和R是邊界if (L>=R) return; //當前區間元素個數<=1則退出int key, i=L, j=R; //i和j是左右兩個數組下標移動//把a數組中隨機一個元素和A[L]交換,快排優化,使得基準值的選取隨機key=A[L]; //key作為樞值參與比較while (i<j){while (i<j && A[j]>key) j--;while (i<j && A[i]<=key) i++;if (i<j) swap(A[i], A[j]); //交換A[i]和A[j]}swap(A[L], A[i]);Qsort(A, L, i-1); //遞歸處理左區間Qsort(A, i+1, R); //遞歸處理右區間}void ans(int A[], n){ //算法代碼Qsort(A, 0, n-1);int i=0;while (i<n && A[i]<=0) i++;if (i==n){ //數組A全是非正數cout<<1;//輸出1 return;}/*到這里,A[i]是數組中最小的正數*/ int t=1;//t從1開始for (int j=i; j<n; j++){ if (t==A[j])continue; if (t+1==A[j])t++;else{ //t+1空缺cout<<t+1; //輸出j-i+1 return;}cout<<t+1;//遍歷完數組,輸出t+1}
}
方法二
解析:
思想借鑒到了 Counting sort 中的方法。既然不能用額外空間,那就只有利用
數組本身,跟 Counting sort 一樣,利用數組的 index 來作為數字本身的索引,把正
數按照遞增順序依次放到數組中。即讓 A[0]=1, A[1]=2, A[2]=3, … , 這樣一來,
最后如果哪個數組元素違反了 A[i]=i+1 即說明 i+1 就是我們要求的第一個缺失的正
數。對于那些不在范圍內的數字,我們可以直接跳過,比如說負數,0,或者超過數組
長度的正數,這些都不會是我們的答案。
思路:
交換數組元素,使得數組中第 i 位存放數值(i+1)。最后遍歷數組,尋找第一
個不符合此要求的元素,返回其下標。整個過程需要遍歷兩次數組,復雜度為 O(n)。
下圖以題目中給出的第二個例子為例,講解操作過程。
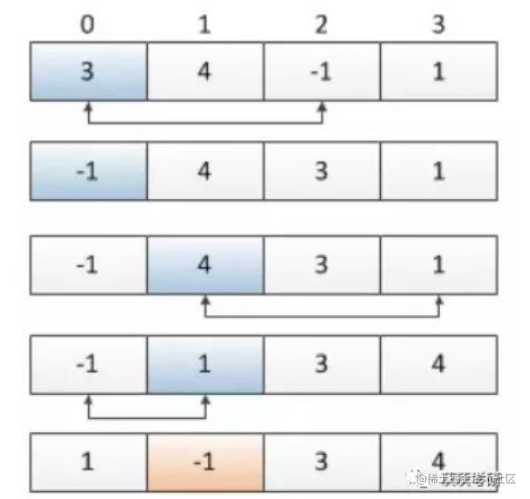
public int firstMissingPositive(int []A){if(A==null||A.length==0){return 1;}for(int i=0;i<A.length;i++){if(A[i]<=A.length && A[i]>0 && A[A[i]-1]!=A[i]){int temp = A[A[i]-1];A[A[i]-1] = A[i];A[i] = temp;i--;}}for(int i=0;i<A.length;i++){it(A[i]!=i+1)return i+1;}return A.length+1;
}
實現中還需要注意一個細節,就是如果當前的數字所對應的下標已經是對應數字了,
那么我們也需要跳過,因為那個位置的數字已經滿足要求了,否則會出現一直來回交
換的死循環。這樣一來我們只需要掃描數組兩遍,時間復雜度是 O(2*n)=O(n),而且
利用數組本身空間,只需要一個額外變量,所以空間復雜度是 O(1)。
補充
Counting sort 基本思想:
對于給定的輸入序列中的每一個元素 x,確定該序列中值小于 x 的元素的個數 。一
旦有了這個信息,就可以將 x 直接存放到最終的輸出序列的正確位置上。它創建一個
長度為這個數據范圍的數組 C,C 中每個元素記錄要排序數組中對應記錄的出現個
數。
下面以示例來說明這個算法:
假設要排序的數組為 A = {1,0,3,1,0,1,1}這里最大值為 3,最小值為 0,那么我們
創建一個數組 C,長度為 4。
然后一趟掃描數組 A,得到 A 中各個元素的總數,并保持到數組 C 的對應單元中。比如 0 的出現次數為 2 次,則 C[0] = 2;1 的出現次數為4 次,則 C[1] = 4。由于 C 是以 A 的元素為下標的,所以這樣一做,A 中的元素在 C中自然就成為有序的了,這里我們可以知道 順序為 0,1,3 (2 的計數為 0)然后我們把這個在 C 中的記錄按每個元素的計數展開到輸出數組 B 中,排序就完成了。
也就是 B[0] 到 B[1] 為 0 B[2] 到 B[5] 為 1 這樣依此類推。
這種排序算法,依靠一個輔助數組來實現,不基于比較,算法復雜度為 O(n) ,但由
于要一個輔助數組 C,所以空間復雜度要大一些,由于計算機的內存有限,所以這種
算法不適合范圍很大的數的排序。
上述為計數排序算法的經典解法,不過這個解法并不是最優的,因為空間復雜度還應
該可以優化,我們完全可以不要那個輸出的數組 B,直接對 C 進行排序。



















