Scikit-learn Python機器學習 - 分類算法

鋒哥原創的Scikit-learn Python機器學習視頻教程：

https://www.bilibili.com/video/BV11reUzEEPH

課程介紹
?

本課程主要講解基于Scikit-learn的Python機器學習知識，包括機器學習概述，特征工程(數據集，特征抽取，特征預處理，特征降維等)，分類算法(K-臨近算法，樸素貝葉斯算法，決策樹等)，回歸與聚類算法(線性回歸，欠擬合，邏輯回歸與二分類，K-means算法)等。

Scikit-learn Python機器學習 - 分類算法 - 樸素貝葉斯

什么是貝葉斯公式？

在學習樸素貝葉斯之前，我們必須先掌握貝葉斯公式

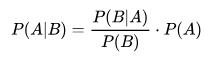
這個公式乍一看，你肯定很懵逼，不過不用怕，我們來解釋和分解下，你就懂了。

這些符號是什么意思？

P(A|B)：在 B 已經發生的情況下，A 發生的概率。這是我們想求的，叫做后驗概率（更新后的信念）。
P(B|A)：在 A 已經發生的情況下，B 發生的概率。這個通常我們從數據中能得到，叫做似然概率。
P(A)：在不知道任何證據（B）的情況下，A 發生的概率。這是我們最初的看法，叫做先驗概率。
P(B)：B 發生的總概率，叫做證據或標準化常量。

我們來推導一下貝葉斯公式

P(AB)=P(A)*P(B|A) A和B同時發生的概率等于P(A)乘以P(B|A)，這個大家應該能理解。

同理 P(AB)=P(B)*P(A|B) A和B同時發生的概率也等于P(B)乘以P(A|B)，相信這個大家也應該能理解。

所以我們能推導出 P(A) * P(B|A) = P(B) * P(A|B) 把右邊的P(B)放到左邊去就推導出了貝葉斯公式。相當大家徹底理解了貝葉斯公式。

貝葉斯公式經典實例-疾病的檢測

這是一個非常著名且反直覺的例子，能完美展示貝葉斯思想的威力。

場景： 假設某種疾病在人群中的發病率是 1%（先驗知識）。現在有一種檢測方法：

如果你確實有病，檢測結果呈陽性（True Positive）的概率是 99%（非常準）。
如果你沒有病，檢測結果呈陽性（False Positive）的概率是 5%（有5%的誤診率）。

問題： 如果一個人去做了檢測，結果是陽性，那么他真正患病的概率到底是多少？

很多人會直覺地認為是99%或者95%，但貝葉斯定理會給我們一個出乎意料的答案。

首先，定義事件：

A：真正患病
B：檢測結果為陽性

我們要求的是：在檢測結果為陽性的情況下，真正患病的概率，即 P(患病 | 陽性)，也就是 P(A|B)。

根據公式，我們需要知道：

P(A) - 先驗概率：在不知道檢測結果時，一個人患病的概率 = 發病率 = 1% = 0.01
P(B|A) - 似然概率：如果一個人真有病，檢測為陽性的概率 = 99% = 0.99
P(B) - 證據：檢測結果為陽性的總概率。這個需要計算一下。

計算 P(B)： 一個人檢測為陽性有兩種可能：

他真有病，并且檢測對了：(0.01 * 0.99)
他其實沒病，但被誤診了：((1 - 0.01) * 0.05)

所以，P(B) = (真有病且測出陽性) + (真沒病但誤診為陽性) P(B) = (0.01 * 0.99) + (0.99 * 0.05) P(B) = 0.0099 + 0.0495 P(B) = 0.0594

現在，將所有值代入貝葉斯公式：

P(A|B) =0.99/0.0594*0.01=0.1667

結論： 即使檢測結果是陽性，你真正患病的概率也只有大約 16.67%！

什么是樸素貝葉斯算法？

樸素貝葉斯（Naive Bayes）算法 是一種基于貝葉斯定理的分類方法，廣泛應用于文本分類（如垃圾郵件識別、情感分析等）和其他機器學習領域。它的核心假設是 特征與特征之間條件相互獨立，即在給定類別的條件下，特征之間沒有任何關系或依賴。

樸素貝葉斯公式

在給定數據集的條件下，樸素貝葉斯定理的公式可以用貝葉斯公式推導出來。假設我們有一個樣本

，這些是特征（例如文本中的單詞頻率、圖像的像素等）。目標是通過這些特征來預測一個類別 C 。

樸素貝葉斯的優缺點

優點：

簡潔高效：樸素貝葉斯方法實現簡單，訓練和預測速度都非常快。
適合高維數據：對于特征維度很高的數據（如文本分類），樸素貝葉斯特別適用，因為它能有效處理大量的特征。
良好的性能：在許多實際問題中，樸素貝葉斯能夠取得不錯的分類效果，特別是在數據特征間獨立性假設基本成立的情況下。

缺點：

條件獨立假設過于簡單：實際數據中，特征之間往往存在依賴關系，而樸素貝葉斯假設特征之間完全獨立，這可能會影響其性能。
對稀疏數據敏感：如果某個類別中某個特征從未出現過，樸素貝葉斯會計算出零概率，導致預測失敗。為了解決這個問題，通常采用平滑技術（如拉普拉斯平滑）來避免零概率的問題。

樸素貝葉斯算法 在實際應用中有著廣泛的使用，尤其適用于文本分類、垃圾郵件檢測、情感分析、推薦系統等任務。由于其計算簡單、高效并且能夠處理大規模數據，樸素貝葉斯常常成為一些領域中首選的算法之一。

樸素貝葉斯算法具體Scikit-learn實例-新聞文本分類預測

MultinomialNB 是 Scikit-learn 中用于多項式分布數據的樸素貝葉斯分類器，特別適合文本分類等離散特征計數的場景。下面我將詳細解釋其構造方法、參數、屬性和方法。

構造方法：

MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)

參數詳解：

alpha : float, 默認=1.0

含義：平滑參數（拉普拉斯平滑/Lidstone平滑）
作用：防止概率計算中出現零值的問題
詳細解釋：
- 當某個特征在某個類別中從未出現時，概率會變為0，導致整個后驗概率為0
- alpha=1 是拉普拉斯平滑（加1平滑）
- 0 < alpha < 1 是Lidstone平滑
- alpha=0 表示不使用平滑（可能導致過擬合和零概率問題）
數學公式：
- 平滑后的條件概率：P(x_i|y) = (N_{yi} + α) / (N_y + α × n)
- 其中 N_{yi} 是特征 i 在類別 y 中的出現次數，N_y 是類別 y 中所有特征的出現次數，n 是特征數量
建議值：通常使用1.0，可以通過交叉驗證調整

fit_prior : bool, 默認=True

含義：是否學習類別先驗概率
作用：控制是否使用訓練數據中的類別分布
詳細解釋：
- fit_prior=True：使用訓練數據中的類別頻率作為先驗概率
- fit_prior=False：使用均勻先驗概率（所有類別概率相等）
數學公式：
- 當 fit_prior=True：P(y) = N_y / N
- 當 fit_prior=False：P(y) = 1 / k (k為類別數)
適用場景：
- 當訓練集類別分布能代表真實分布時，使用True
- 當訓練集類別不平衡或不能代表真實分布時，可考慮使用False

class_prior : array-like of shape (n_classes,), 默認=None

含義：類別的先驗概率
作用：手動指定各類別的先驗概率
詳細解釋：
- 如果指定了此參數，fit_prior參數將被忽略
- 數組長度必須等于類別數量
- 概率值應該總和為1（但算法會自動歸一化）
示例：對于二分類問題，可以設置class_prior=[0.7, 0.3]

我們來看下具體示例：

from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics import accuracy_score, classification_report
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB# 1,加載數據
news = fetch_20newsgroups(subset='all')# 2,數據預處理
X_train, X_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.2)  # 劃分訓練集和測試集tfidfVectorizer = TfidfVectorizer()  # 特征抽取 TF-IDF
X_train_scaled = tfidfVectorizer.fit_transform(X_train)  # fit計算生成模型
X_test_scaled = tfidfVectorizer.transform(X_test)  # # 使用訓練集的參數轉換測試集# 3,創建和訓練LogisticRegression模型
model = MultinomialNB()
model.fit(X_train_scaled, y_train)  # 使用訓練數據擬合（訓練）模型# 4,進行預測并評估模型
y_pred = model.predict(X_test_scaled)  # 在測試集上進行預測
print('模型預測值：', y_pred)
print('正確值   ：', y_test)accuracy = accuracy_score(y_test, y_pred)  # 計算準確率
print(f'測試集準確率：{accuracy:.2f}')
print('分類報告：\n', classification_report(y_test, y_pred, target_names=news.target_names))

運行結果：

模型預測值： [ 0 18 11 ...  5 15 10]
正確值   ： [ 0 18 11 ...  5  2  9]
測試集準確率：0.85
分類報告：precision    recall  f1-score   supportalt.atheism       0.91      0.73      0.81       170comp.graphics       0.87      0.77      0.81       193comp.os.ms-windows.misc       0.87      0.80      0.83       192
comp.sys.ibm.pc.hardware       0.68      0.88      0.77       181comp.sys.mac.hardware       0.97      0.86      0.91       205comp.windows.x       0.95      0.86      0.90       205misc.forsale       0.90      0.70      0.79       185rec.autos       0.93      0.89      0.91       205rec.motorcycles       0.95      0.96      0.95       206rec.sport.baseball       0.95      0.94      0.94       194rec.sport.hockey       0.91      0.98      0.94       200sci.crypt       0.78      0.97      0.86       200sci.electronics       0.92      0.86      0.89       188sci.med       0.97      0.86      0.92       200sci.space       0.89      0.97      0.93       199soc.religion.christian       0.56      0.99      0.72       203talk.politics.guns       0.69      0.97      0.81       163talk.politics.mideast       0.95      0.97      0.96       205talk.politics.misc       1.00      0.53      0.69       158talk.religion.misc       1.00      0.21      0.35       118accuracy                           0.85      3770macro avg       0.88      0.84      0.84      3770weighted avg       0.88      0.85      0.85      3770Process finished with exit code 0