一 概念
1 決策節點
通過條件判斷而進行分支選擇的節點。
將樣本的屬性值,也就是特征值與決策節點上的值進行比較,從而判斷它的流向。
2 葉子節點
沒有子節點的節點,表示最終的決策結果。
3 決策樹的深度
所有節點的最大層次數
決策樹具有一定的層次結構,根節點的層次數定為0,從下面開始每一層子節點層次數增加。
4 決策樹優缺點
優點:可視化、可解釋能力、對算力要求低;
缺點:容易產生過擬合,所以不要把深度調整太大;
二 基于信息增益決策樹的建立
信息增益決策樹傾向于選擇取值較多的屬性。
有些情況下,這類屬性可能不會提供太多有價值的信息,算法只能對描述屬性為離散型屬性的數據集構造決策樹。
1 信息熵
信息熵描述的是不確定性。
信息熵越大,不確定性越大。信息熵的值越小,則樣本集合D的純度越高。
假設樣本集合D共有N類,第K類樣本所占比例為pk,則樣本集合D的信息熵為:
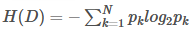
2 信息增益
信息增益是一個統計量,用來描述一個屬性區分數據樣本的能力。
信息增益越大,那么決策樹就會越簡潔。
信息增益的程度用信息上的變化程度來衡量:IG(Y|X)=H(Y)-H(Y|X)≥0
3 信息增益決策樹建立步驟
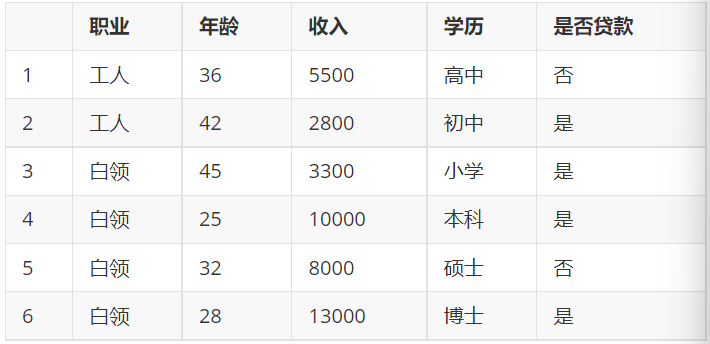
3.1 計算根節點的信息熵
上表把是否貸款分為2類樣本:“是”占2/3,“否”占1/3;
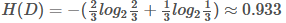
3.2 計算屬性的信息增益
3.2.1職業 屬性的信息增益
IG(D,"職業“)
在職業中,工人占1/3,工人中,是否貸款各占1/2,所以: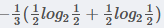
在職業中,白領占2/3, ?白領中,是貸款占3/4, 不貸款占1/4, 所以有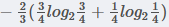
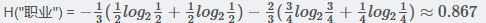

3.2.2?年齡 屬性的信息增益
(以35歲為界)

3.2.3 收入 屬性的信息增益
(以10000為界,大于等于10000為一類)
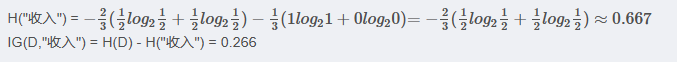
3.2.4 學歷 屬性的信息增益
(以高中為界, 大于等于高中的為一類)
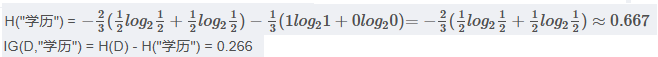
注意:?
以上年齡使用35為界,收入使用10000為界,學歷使用高中為界。
實計API使用中,會有一個參數"深度", 屬性中具體以多少為界會被根據深度調整。
3.3 劃分屬性
對比屬性信息增益發現,"收入"和"學歷"相等,并且是最高的,所以我們就可以選擇"學歷"或"收入"作為第一個決策樹的節點, 接下來我們繼續重復3.1、3.2的做法繼續尋找合適的屬性節點。
三 基于基尼指數決策樹的建立
基尼指數是指決策樹算法中用于評估數據集純度的一種度量,衡量的是數據集的不純度,也可以說是分類的不確定性。
在構建決策樹時,基尼指數被用來決定如何對數據集進行最優劃分,以減少不純度。
對于一個二分類問題,如果一個節點包含的樣本屬于正類的概率是 (p),則屬于負類的概率是 (1-p)。
這個節點的基尼指數 (Gini(p)) 定義: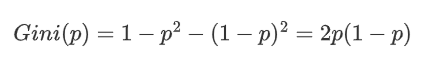
對于多分類問題,如果一個節點包含的樣本屬于第 k 類的概率是 p_k,則節點的基尼指數定義為:
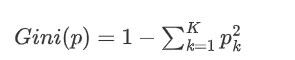
3.1 基尼指數的意義
1、當一個節點的所有樣本都屬于同一類別,基尼指數為0,表示純度最高。
2、當一個節點的樣本均勻分布在所有類別時,基尼指數最大,表示純度最低。
3.2 決策樹中的應用
構建決策樹的時候,希望每個內部節點的子節點能更純,也就是基尼指數更小。
那么選擇分割特征和分割點的目標是使子節點的平均基尼指數最小化。具體就是對一個特征,我們計算其所有的可能的分割點對應的子節點的加權平均基尼,選擇最小化這個值的分割點。這個過程會在所有特征中重復,知道找到最佳的分割特征和分割點。
考慮一個數據集D,其中包含N個樣本,特征A將數據集分割為|D1|和|D2|,則特征A的基尼指數為:,其中|D1|和|D2|分別是子集D1和D2的樣本數量。
通過這樣的方式,決策樹算法逐步構建一棵樹,每層的節點都盡可能減少基尼指數,最終達到對數據集的有效分類。
四 API
class sklearn.tree.DecisionTreeClassifier(....)參數:
criterion "gini" "entropy” 默認為="gini"?
當criterion取值為"gini"時采用 基尼不純度(Gini impurity)算法構造決策樹,
當criterion取值為"entropy”時采用信息增益( information gain)算法構造決策樹.
max_depth?? ?int, 默認為=None ?樹的最大深度
# 可視化決策樹
function sklearn.tree.export_graphviz(estimator, out_file="iris_tree.dot", feature_names=iris.feature_names)參數:
estimator決策樹預估器
out_file生成的文檔
feature_names節點特征屬性名
功能:
把生成的文檔打開,復制出內容粘貼到"http://webgraphviz.com/"中,點擊"generate Graph"會生成一個樹型的決策樹圖






)









)


