---

一、相交鏈表

相交鏈表

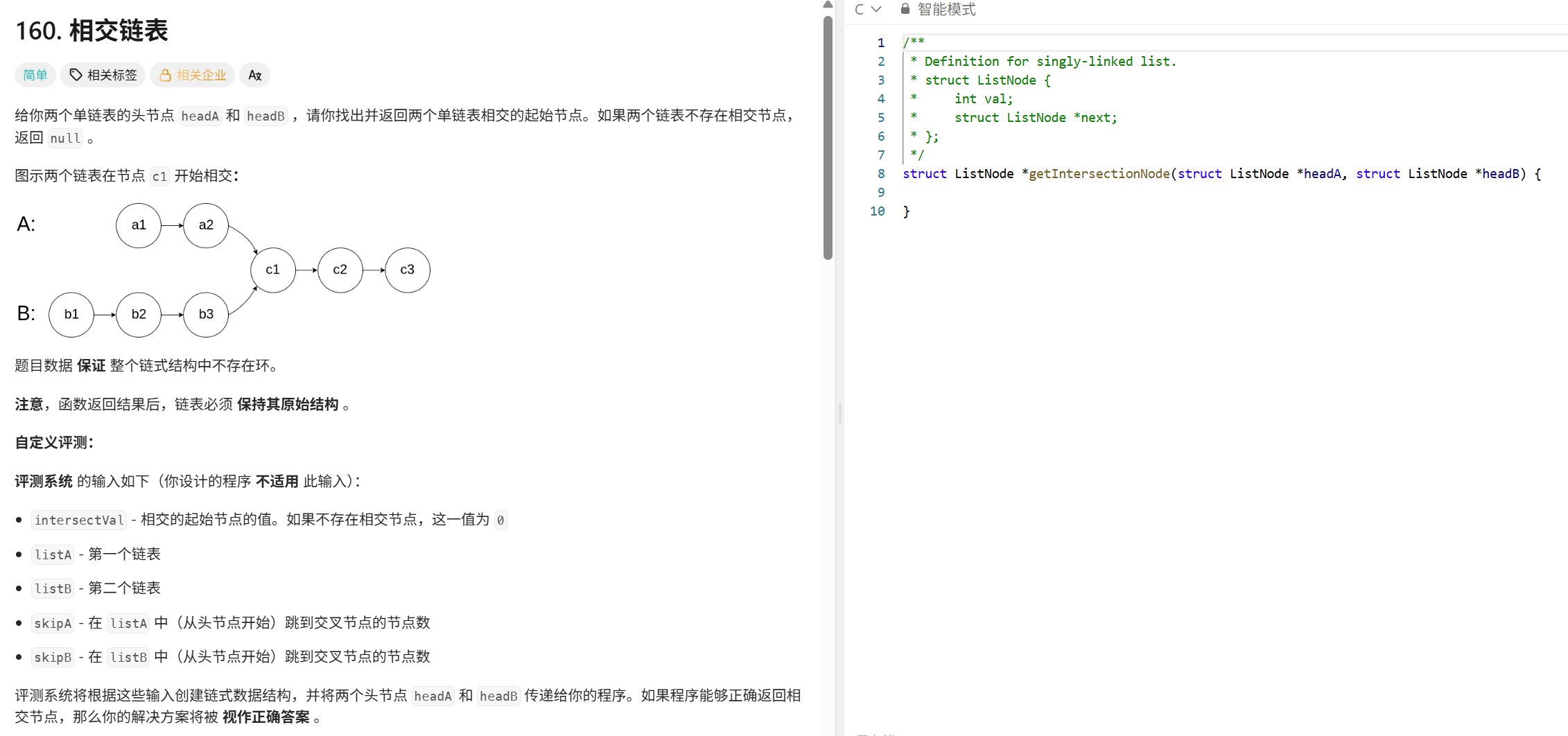
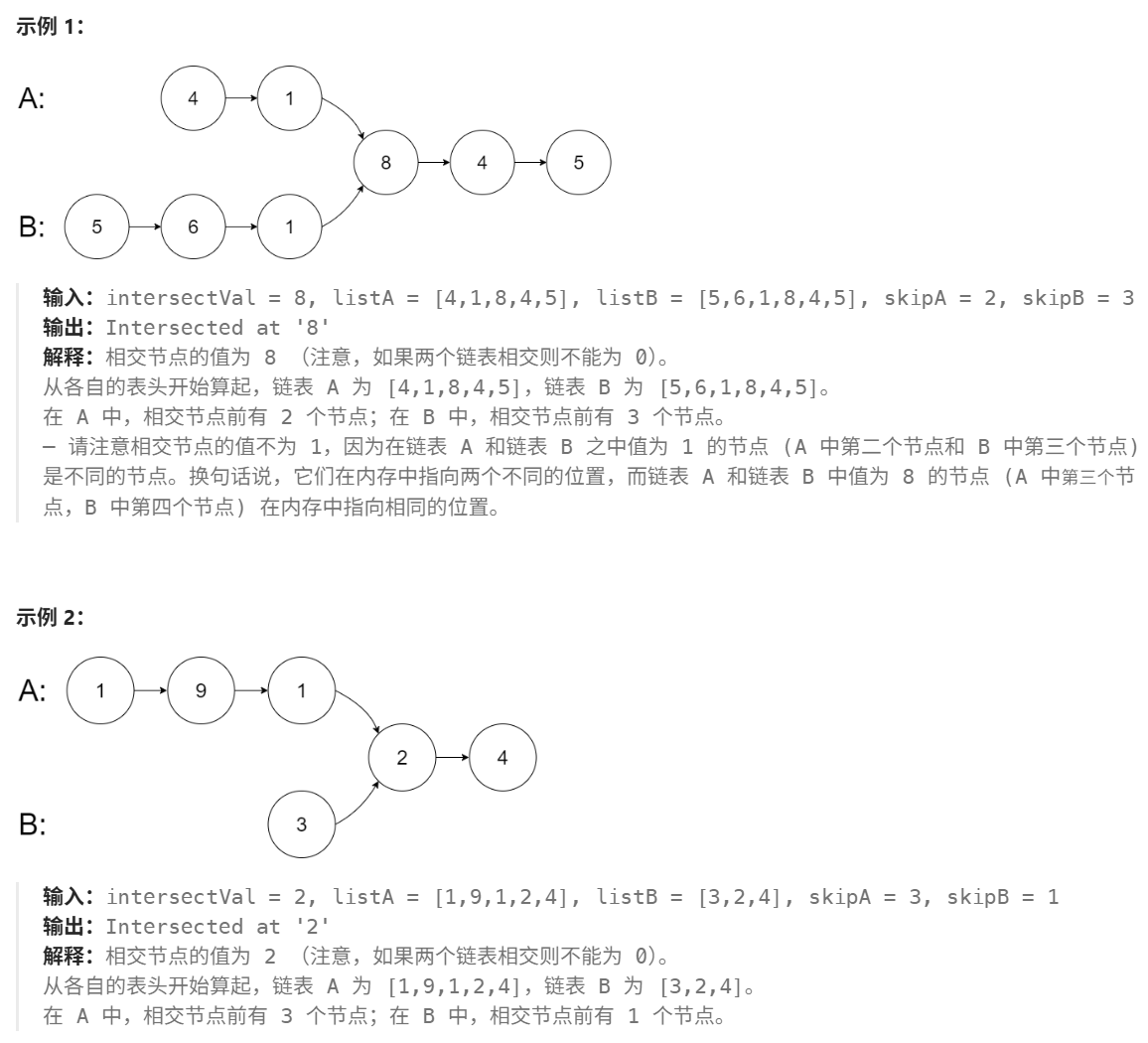
首先理解什么是鏈表相交，相交即存在共用的節點，鏈表相交有三種情況，

1. 中間位置相交
2. 頭部就開始相交
3. 尾部相交

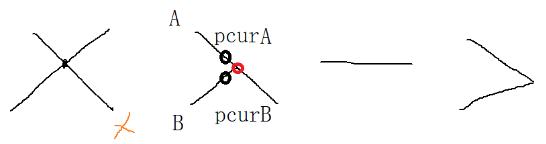
如圖pcurA和pcurB就都有一個next指針指向同一個節點
這幾種鏈表結構畫成圖如下

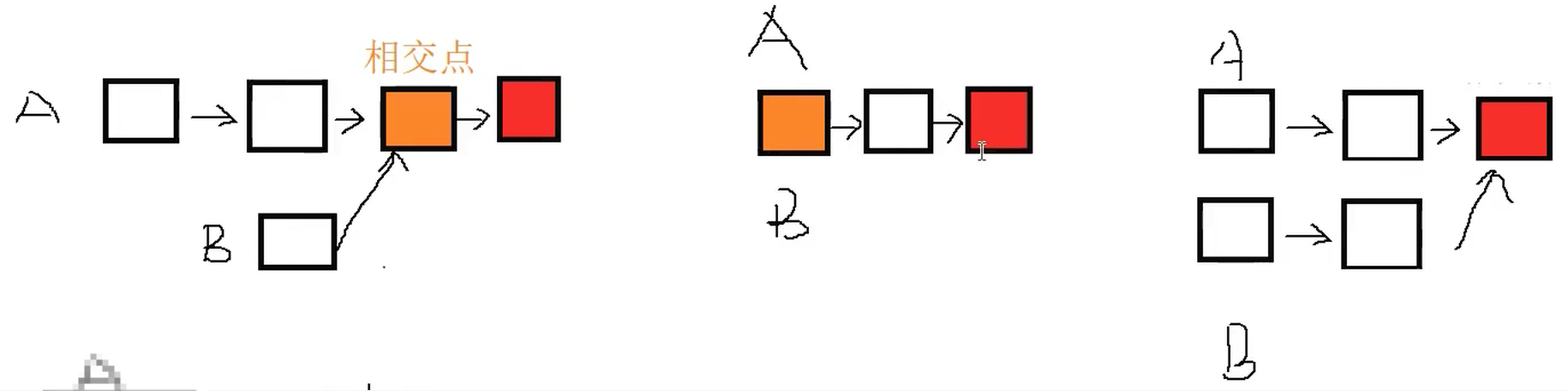
為什么說鏈表中沒有第一種結構呢？

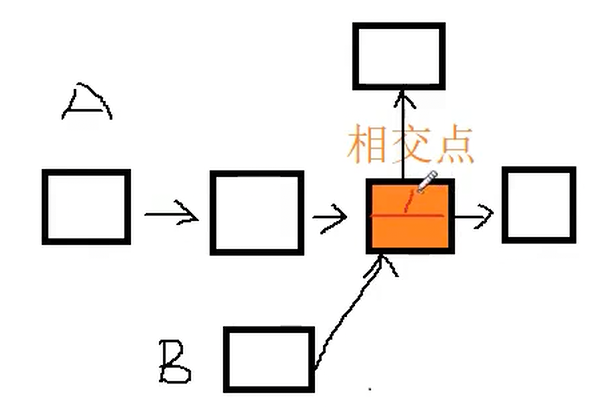
相交點即一個節點，其包括兩個組成部分，一個是存儲的數據，一個是next指針，一個節點的next指針不可能同時指向兩個節點

這里也可以總結出兩個鏈表相交的條件：
兩個鏈表的尾節點相同，兩個鏈表一定相交

思路：求兩個鏈表的長度，長鏈表先走長度差步，長短鏈表開始同步遍歷，找相同的節點

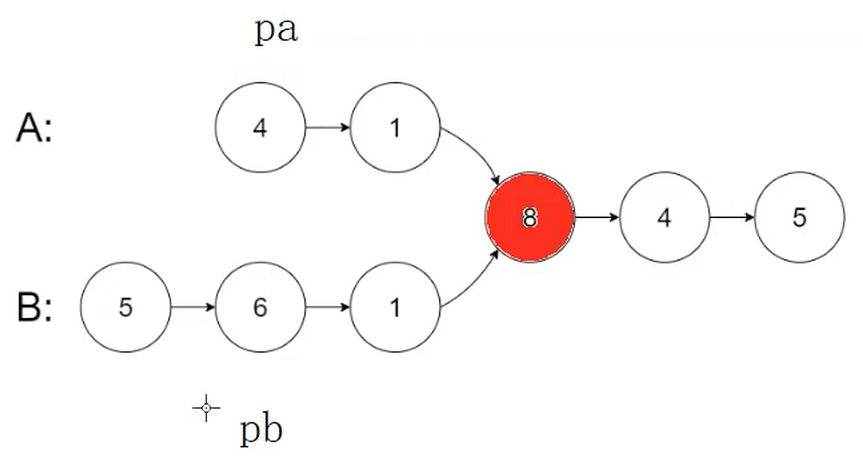
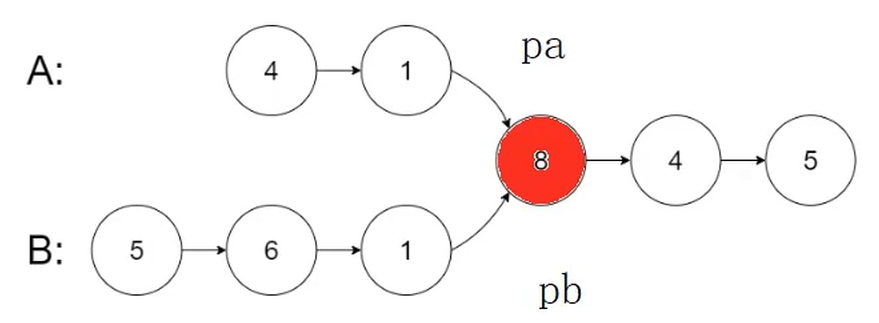
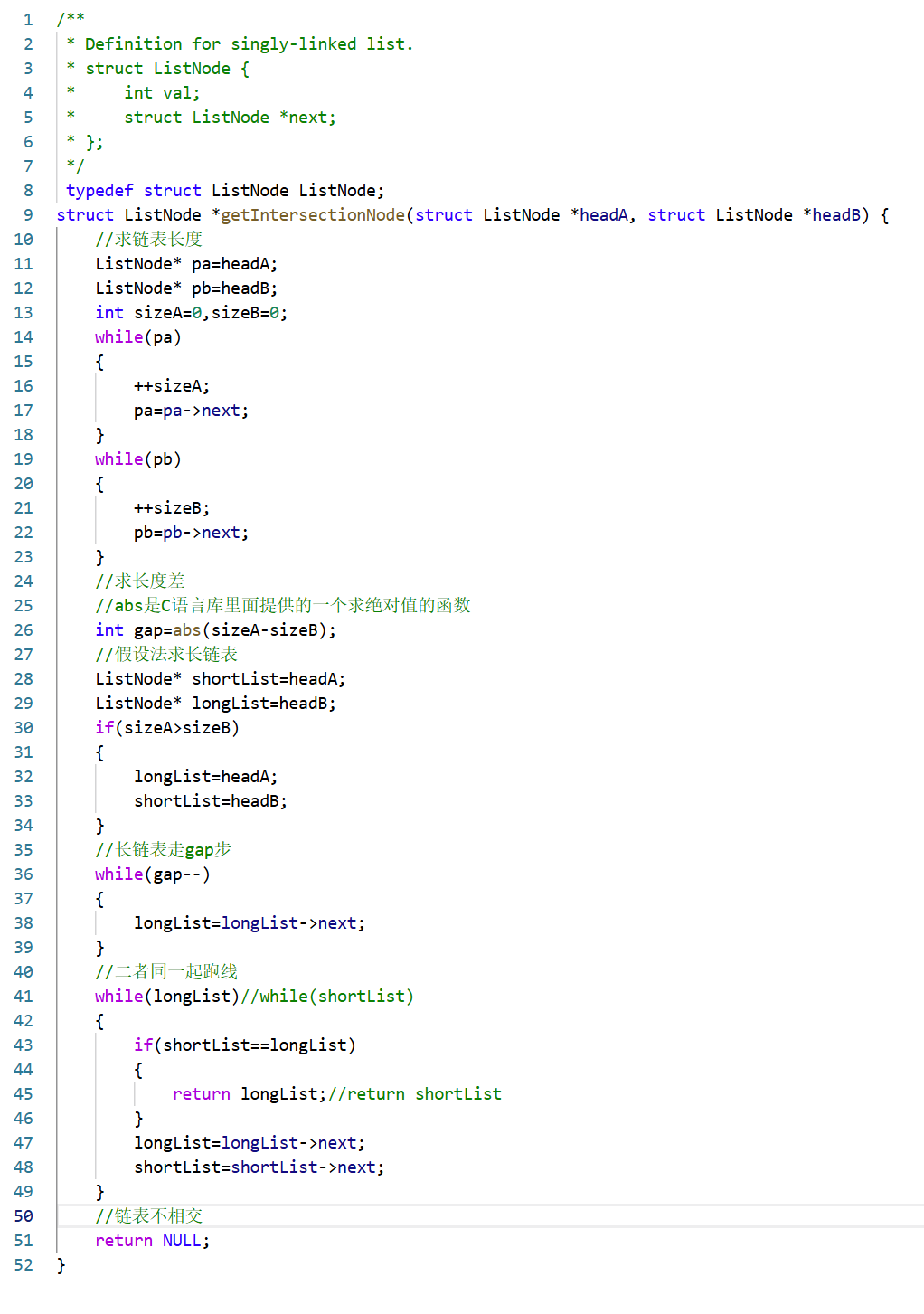
return NULL把結果給遠程服務器，會把結果包裝一下，最后輸出沒有相交點

---

二、環形鏈表I

環形鏈表I
簡單來說，如果鏈表帶環，鏈表尾節點的next指針不會直接置為空，且遍歷鏈表是一個死循環的
補充：環形鏈表的尾節點甚至可以指向自己

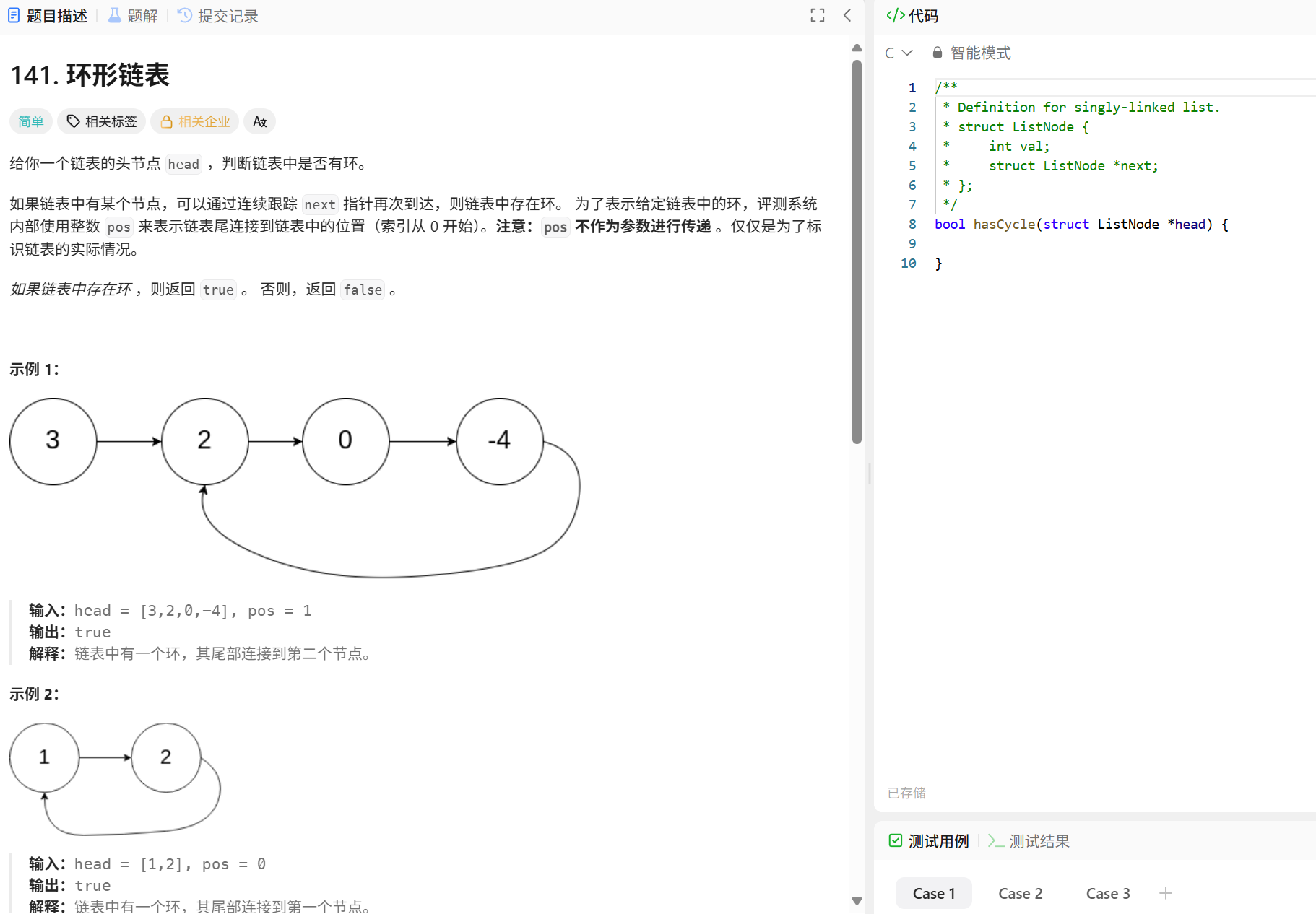
思路：快慢指針，慢指針每次走一步，快指針每次走兩步，如果slow和fast指向同一節點，說明鏈表帶環，類似于表盤的時鐘和分鐘

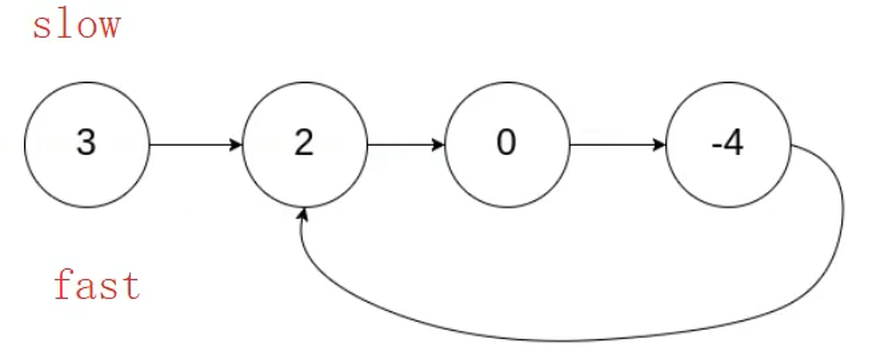
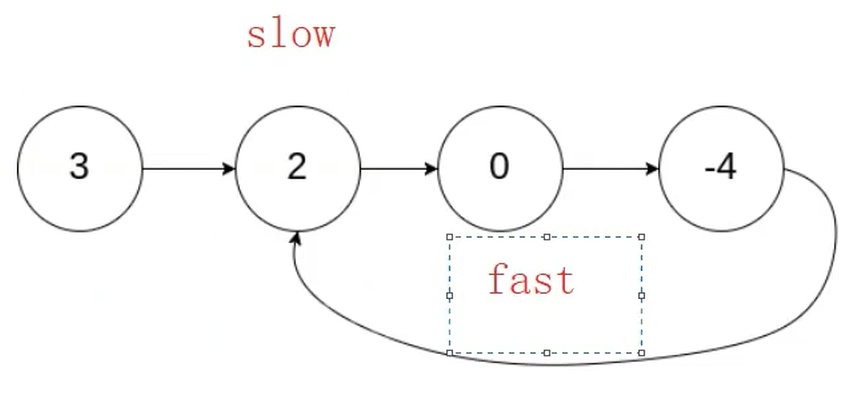
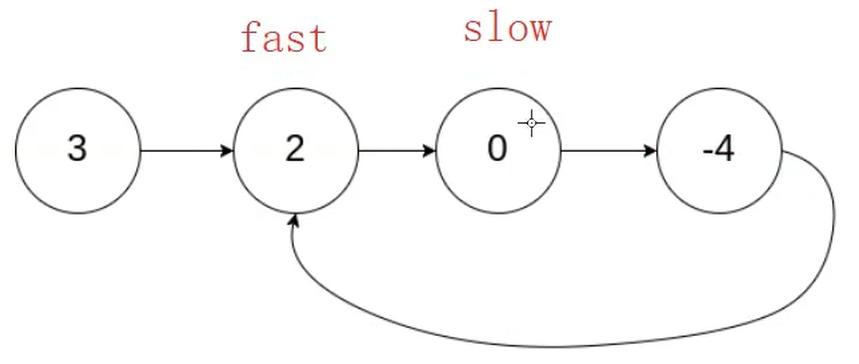
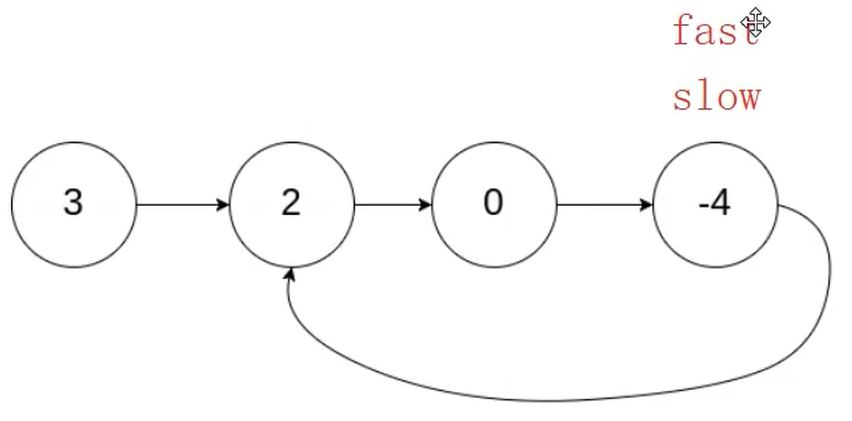
補充：快慢指針在一個鏈表上開始遍歷，如果該鏈表不是帶環的，那節點一定為空，這種鏈表又分為奇數和偶數情況

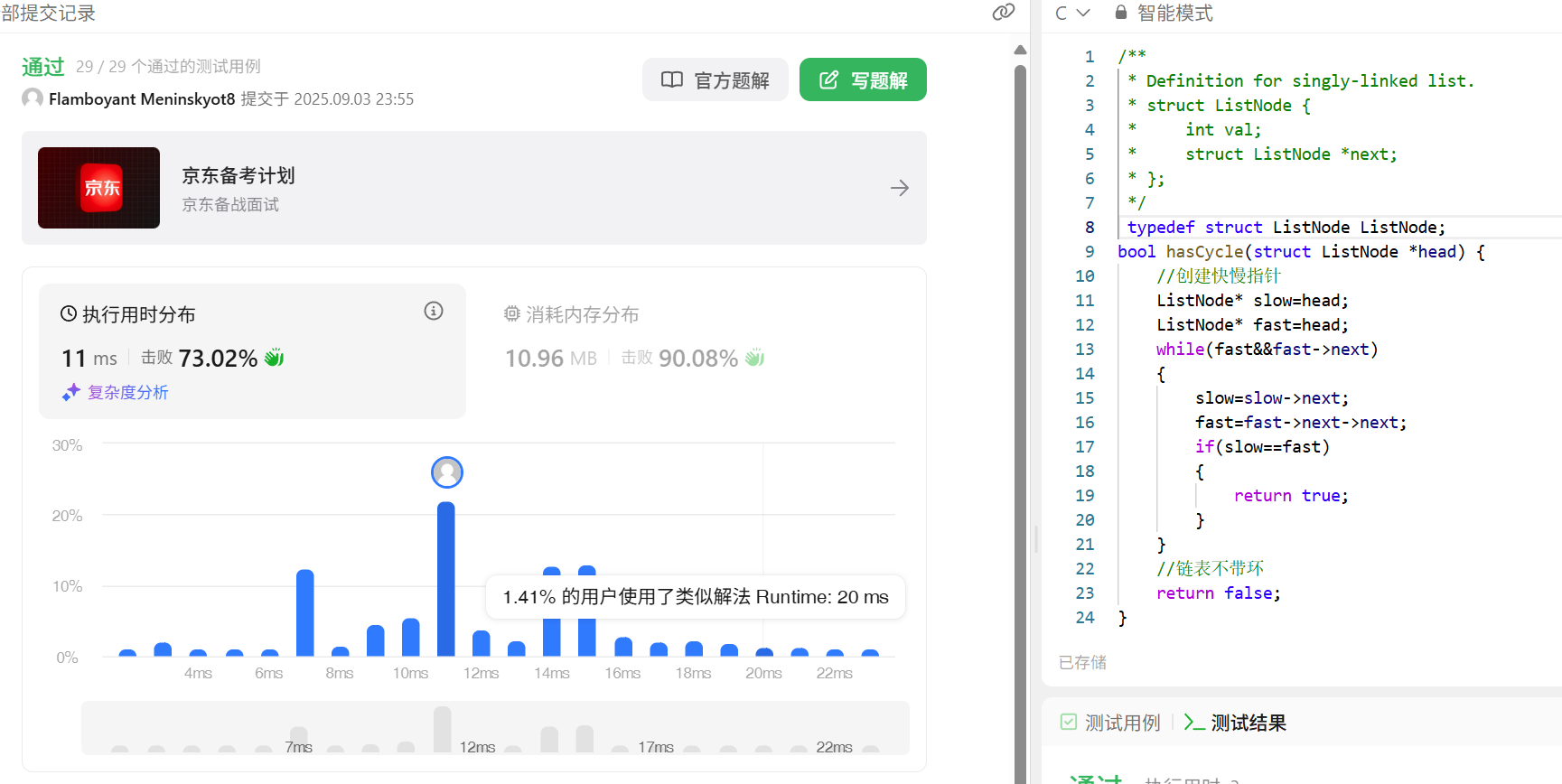
證明1：接下來最重要的部分來了，為什么在帶環鏈表里面，慢指針每次走一步，快指針每次走兩步，最終一定會相遇

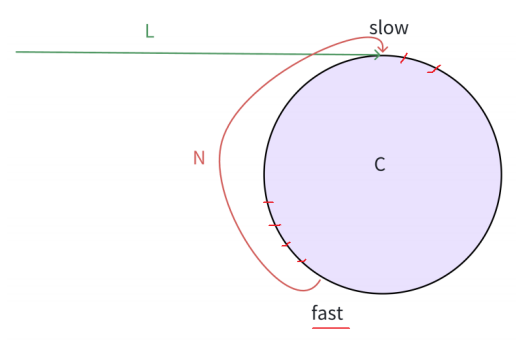
圖中slow的位置是入環點，入環之后是一個圓，其運動路徑是一個圓。假設slow走到入環點，fast已經走到如圖位置，此時slow和fast之間的距離最大，為N，此時slow走一步，fast走兩步

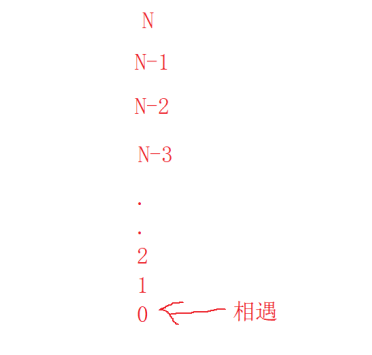
二者之間距離變為N+1-2=N-1，繼續就是N-2，N-3，如圖最后變為0，也就是相遇，所以慢指針走一步，快指針走兩步，如果是環形鏈表一定會相遇，就像表盤當中的時針和分針一樣。

證明2：在環形鏈表中，慢指針每次走一步，快指針每次走3，4，5步，快慢指針在環形鏈表中還會相遇嗎？

這里就以慢指針每次走一步，快指針每次走三步為例，依舊假設此時slow剛入環，此時slow和fast之間的距離最大，為N。
此時slow走一步，fast走三步，二者距離變為N+1-3=N-2。再一次就是N-2+1-3=N-4。

此時二者之間距離想要變為0，N必須要是偶數才行，這一圈才可以追上。若N為奇數（比如說N=7），7-2=5，5-2=3，3-2=1，1-2=-1。這一圈便追不上了
這樣本來fast在追slow，二者距離變為-1，fast在slow前面，變為slow追fast。
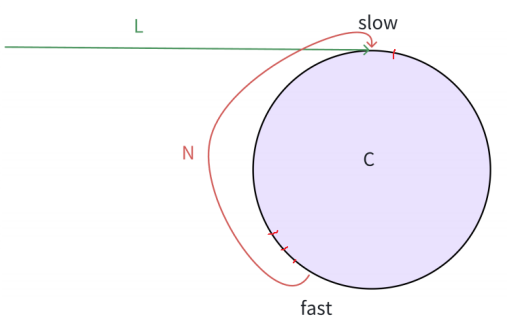
當套圈之后，slow和fast的距離便變為了下圖紅線的長度，加入一圈的周長是C，套圈之后二者的距離便變為了C-1

在C-1的距離又要slow走一步，fast走三步，繼續開始追逐

如果會相遇，說明在環形鏈表里面，fast走三步也能判斷鏈表是否是帶環的，反之

接下來就要證明C-1到底是奇數還是偶數

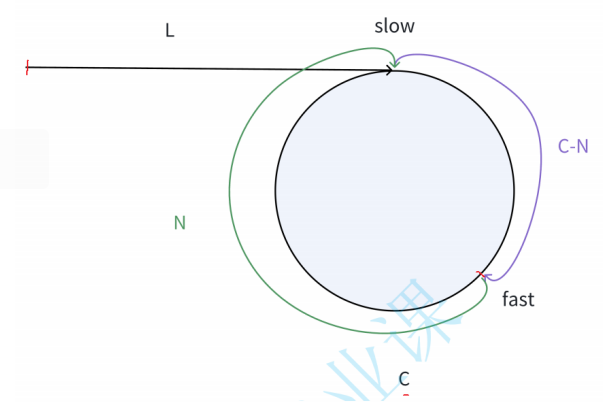
這是在第二圈開始追逐，這里fast的位置不代表fast第一圈入環之后到此處，slow就入環，在此之前fast可能已經走了好幾圈，下圖給出fast和slow的路程關系

由于快指針無論在圈里走幾圈，都不影響其在圈里的位置，所以（n+1）可以忽略掉，就剩下C-N，前面明確的規定N是個奇數，所以C也一定為奇數。

所以得出結論N為奇數，C也一定為奇數，所以在下一圈，快慢指針也一定會相遇

最終結論就是下圖：

---

三、環形鏈表II

環形鏈表II

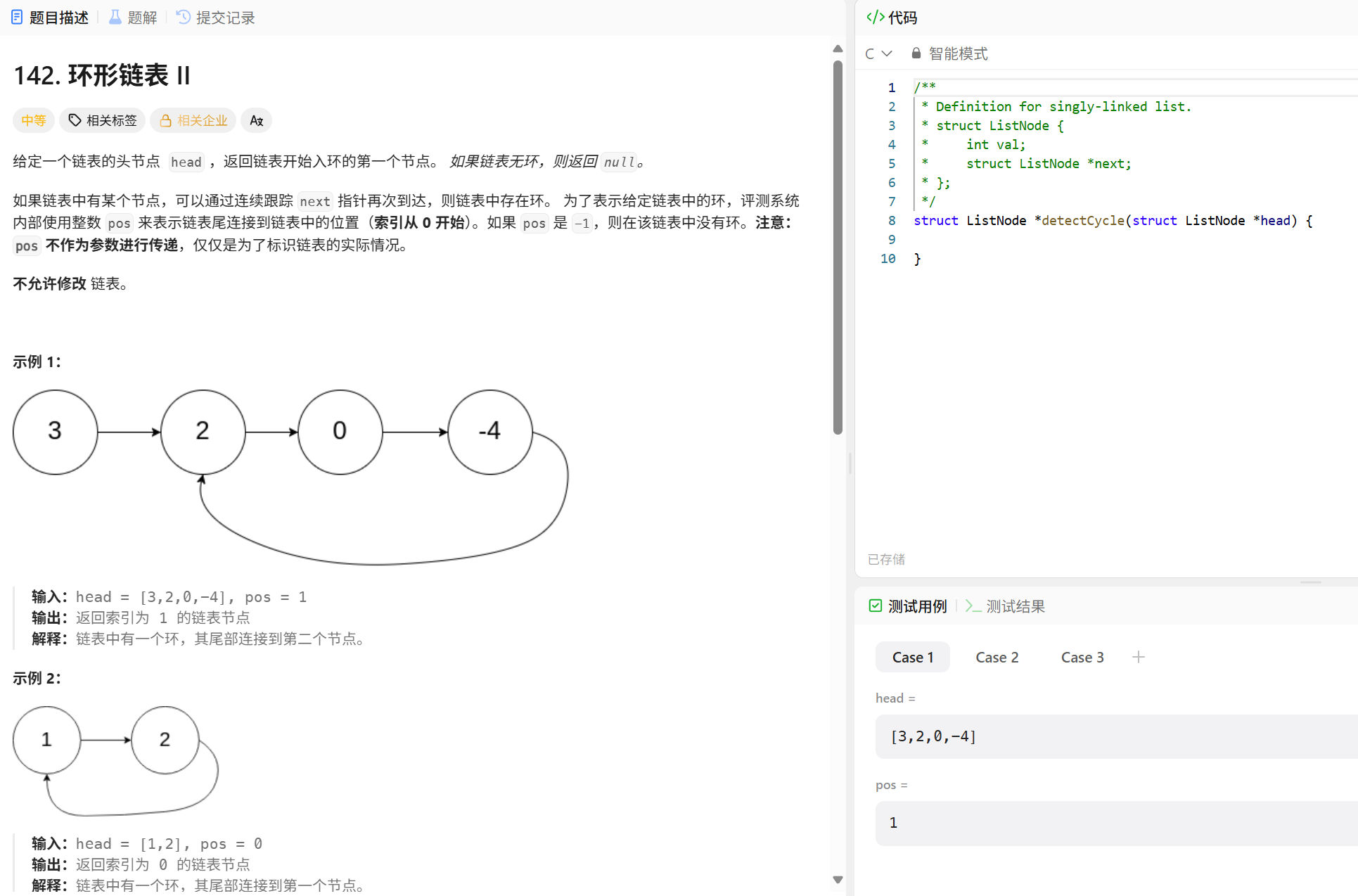
前一道題用快慢指針判斷了鏈表是否帶環，如果是一個帶環的鏈表，快慢指針一定會相遇，但是相遇節點不一定是入環節點，可以是環內的任意一個節點

思路：首先，快慢指針一定會在環里相遇，相遇點到入環節點的距離 == 頭節點到入環節點的距離

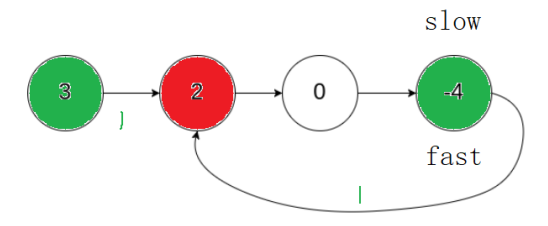
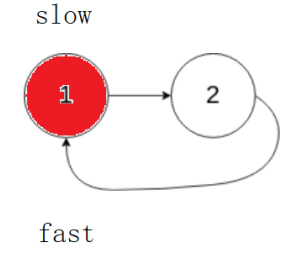
接下來要找起始節點，就一個從頭出發，一個從相遇點出發，同步遍歷，當走到了同一個節點，那這個節點一定是入環節點

代碼如下：

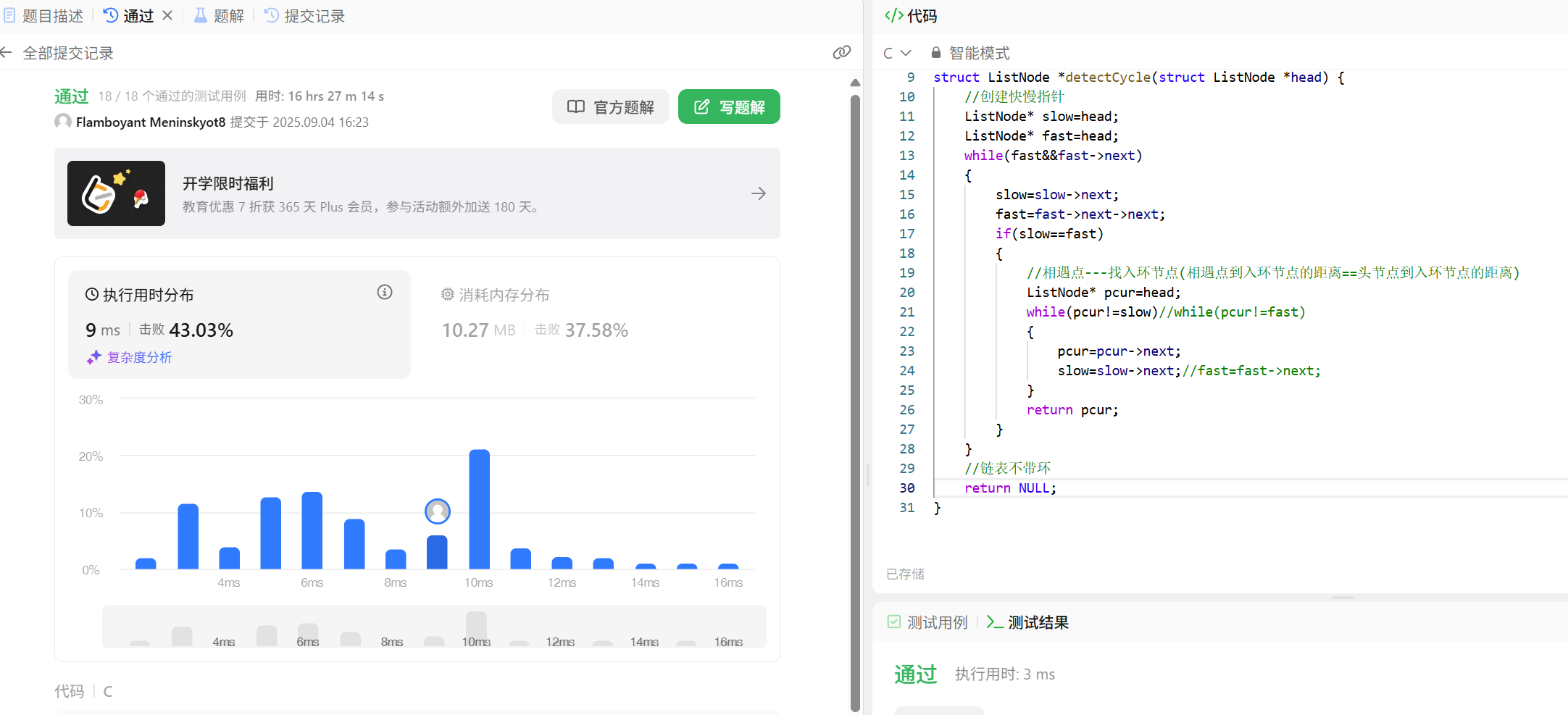
證明：為什么在帶環鏈表中，快慢指針相遇點到入環節點的距離 == 頭節點到入環節點的距離

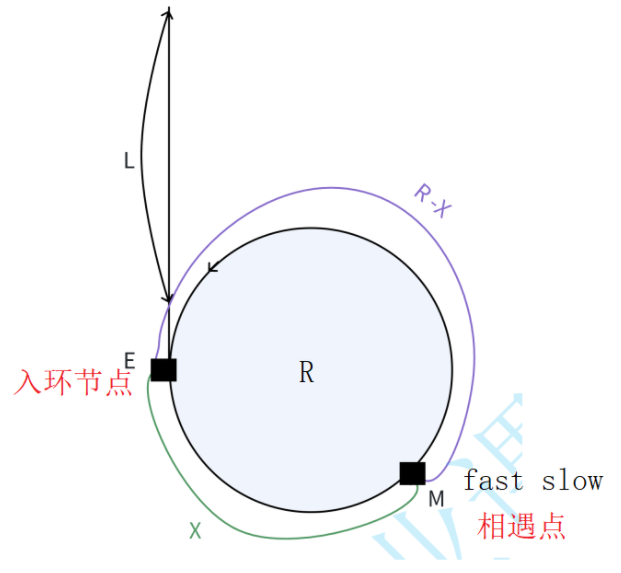
圖中有一處標注有些偏差，頭節點到入環節點的距離為L，假設環的周長為R

（n-1）R是快指針在環里面饒了多少圈，快指針無論繞多少圈都是在相遇點和slow相遇，所以（n-1）R可以忽略，所以最后得出紅字部分結論

---

總結

真寫爽了，數據結構這部分的題寫的想吐了，創作不易，三連支持~