《算法導論》第 16 章

?????????大家好！今天我們來深入探討《算法導論》第 16 章的核心內容 —— 貪心算法。貪心算法是一種在每一步選擇中都采取在當前狀態下最好或最優（即最有利）的選擇，從而希望導致結果是全局最好或最優的算法。它在許多優化問題中都有廣泛應用，如活動安排、哈夫曼編碼、最小生成樹等。

????????接下來，我們將按照教材的結構，逐一講解各個知識點，并提供完整的 C++ 代碼實現，幫助大家更好地理解和應用貪心算法。

16.1 活動選擇問題

????????活動選擇問題是貪心算法的經典應用案例，問題描述如下：

????????問題：?假設有 n 個活動，這些活動共享同一個資源（如會議室），而這個資源在同一時間只能供一個活動使用。每個活動 i 都有一個開始時間 s [i] 和結束時間 f [i]，其中 0 ≤ s [i] < f [i] < ∞。如果兩個活動的時間區間不重疊，則它們是兼容的。活動選擇問題就是要選擇出一個最大的兼容活動集。

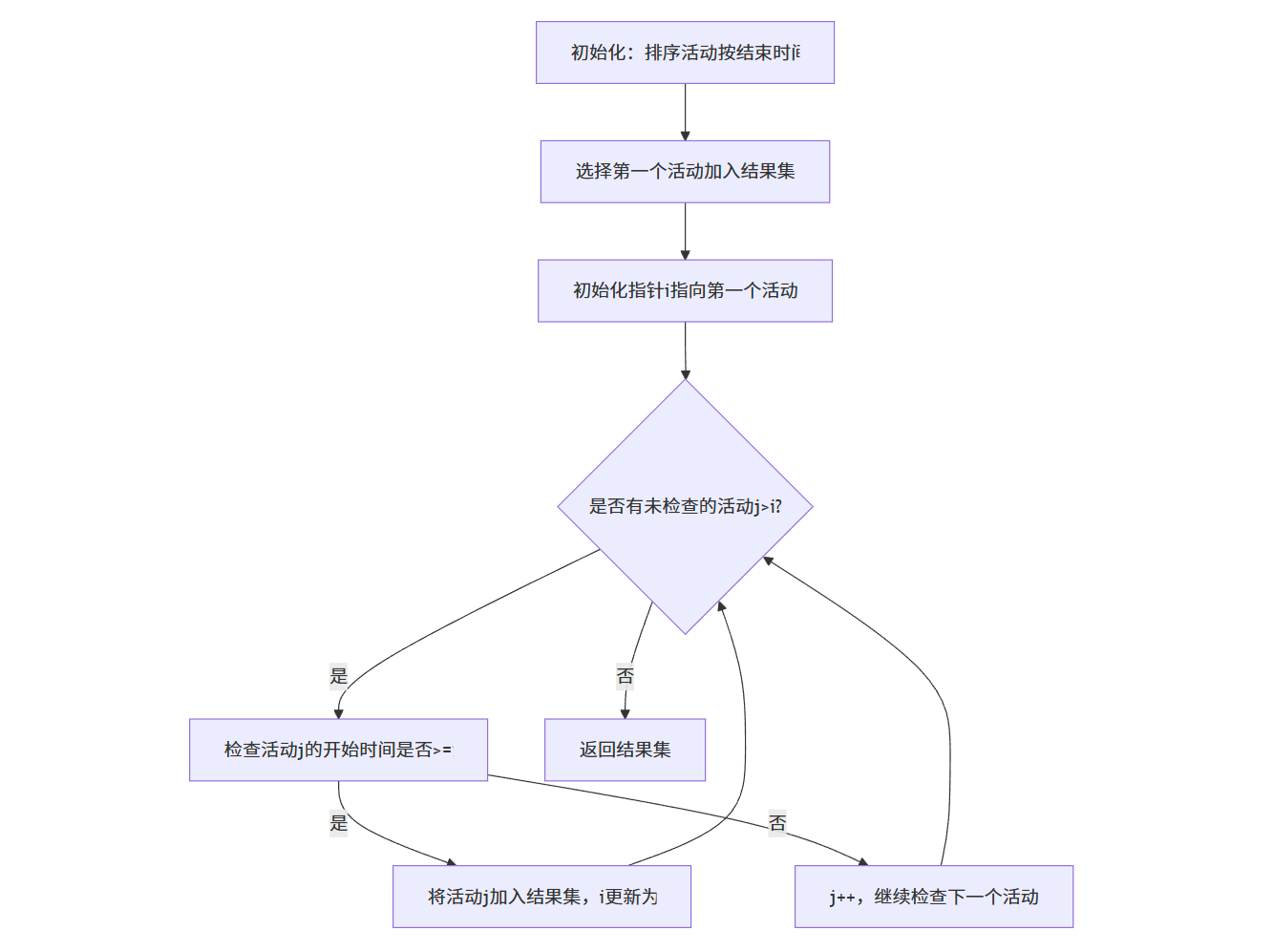
貪心策略分析

對于活動選擇問題，有多種可能的貪心策略：

選擇最早開始的活動
選擇最短持續時間的活動
選擇最晚開始的活動
選擇最早結束的活動

????????經過分析，選擇最早結束的活動這一策略能夠得到最優解。其核心思想是：盡早結束當前活動，以便為后續活動留出更多時間。

代碼實現

下面是活動選擇問題的 C++ 實現，包括遞歸版本和迭代版本：

#include <iostream>
#include <vector>
#include <algorithm>using namespace std;// 活動結構體：開始時間、結束時間、活動編號
struct Activity {int start;int finish;int index;
};// 按結束時間升序排序的比較函數
bool compareFinish(const Activity& a, const Activity& b) {return a.finish < b.finish;
}/*** 迭代版本的活動選擇算法* @param activities 活動列表* @return 選中的活動索引列表*/
vector<int> selectActivitiesIterative(vector<Activity>& activities) {// 按結束時間排序sort(activities.begin(), activities.end(), compareFinish);vector<int> selected;int n = activities.size();// 選擇第一個活動selected.push_back(activities[0].index);int lastSelected = 0;// 依次檢查后續活動for (int i = 1; i < n; i++) {// 如果當前活動的開始時間 >= 最后選中活動的結束時間，則選擇該活動if (activities[i].start >= activities[lastSelected].finish) {selected.push_back(activities[i].index);lastSelected = i;}}return selected;
}/*** 遞歸版本的活動選擇算法* @param activities 活動列表（已排序）* @param index 當前檢查的索引* @param n 活動總數* @param selected 已選中的活動索引列表*/
void selectActivitiesRecursive(const vector<Activity>& activities, int index, int n, vector<int>& selected) {// 找到第一個與最后選中活動兼容的活動int i;for (i = index; i < n; i++) {if (i == 0 || activities[i].start >= activities[selected.back()].finish) {break;}}if (i < n) {// 選擇該活動selected.push_back(activities[i].index);// 遞歸選擇剩余活動selectActivitiesRecursive(activities, i + 1, n, selected);}
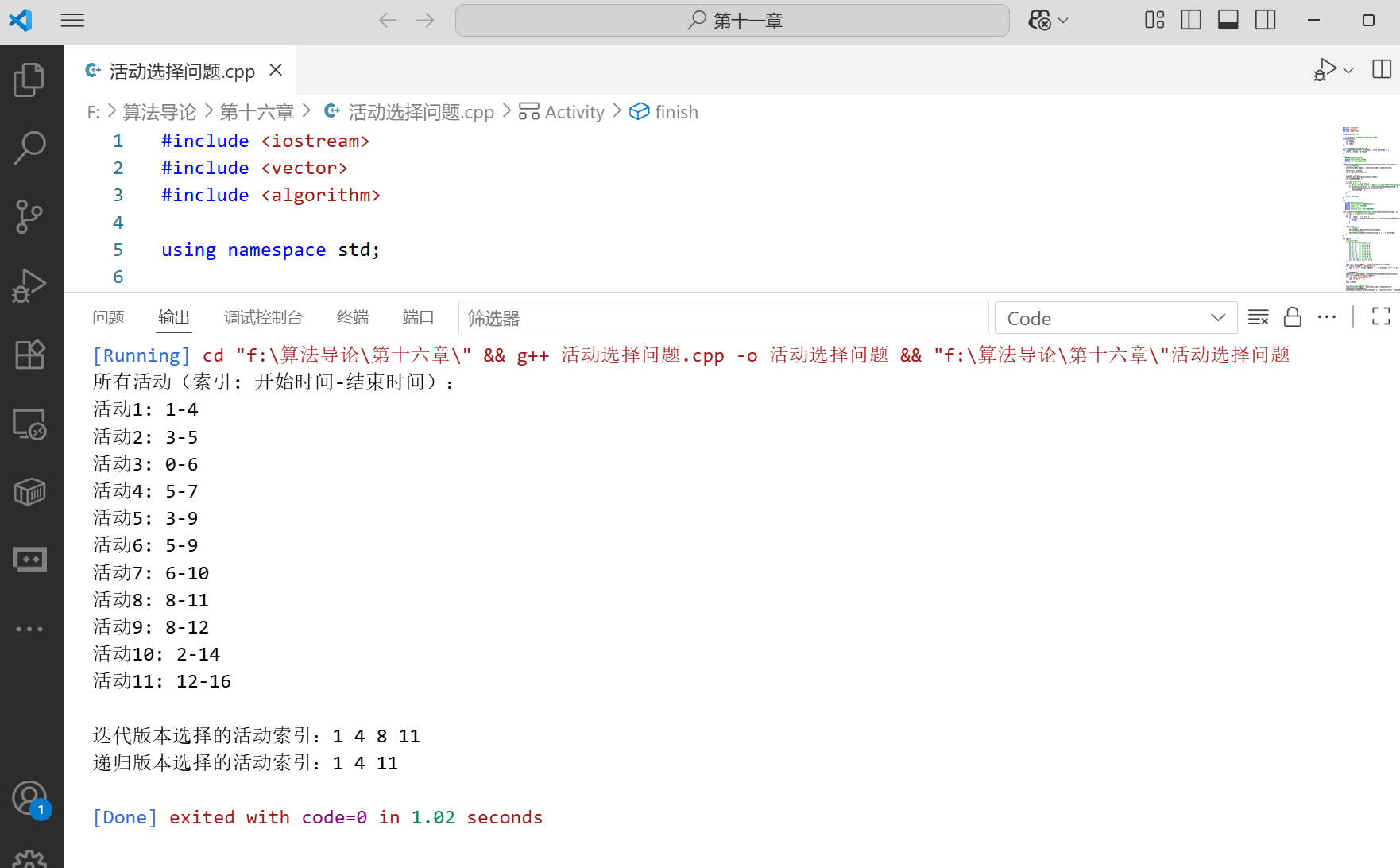
}int main() {// 示例活動數據vector<Activity> activities = {{1, 4, 1},   // 活動1: 1-4{3, 5, 2},   // 活動2: 3-5{0, 6, 3},   // 活動3: 0-6{5, 7, 4},   // 活動4: 5-7{3, 9, 5},   // 活動5: 3-9{5, 9, 6},   // 活動6: 5-9{6, 10, 7},  // 活動7: 6-10{8, 11, 8},  // 活動8: 8-11{8, 12, 9},  // 活動9: 8-12{2, 14, 10}, // 活動10: 2-14{12, 16, 11} // 活動11: 12-16};cout << "所有活動（索引: 開始時間-結束時間）：" << endl;for (const auto& act : activities) {cout << "活動" << act.index << ": " << act.start << "-" << act.finish << endl;}// 測試迭代版本vector<int> selectedIter = selectActivitiesIterative(activities);cout << "\n迭代版本選擇的活動索引：";for (int idx : selectedIter) {cout << idx << " ";}cout << endl;// 測試遞歸版本（需要先排序）sort(activities.begin(), activities.end(), compareFinish);vector<int> selectedRecur;selectActivitiesRecursive(activities, 0, activities.size(), selectedRecur);cout << "遞歸版本選擇的活動索引：";for (int idx : selectedRecur) {cout << idx << " ";}cout << endl;return 0;
}

代碼說明

首先定義了Activity結構體來存儲活動的開始時間、結束時間和索引
實現了按結束時間排序的比較函數compareFinish
迭代版本算法：
- 先對活動按結束時間排序
- 選擇第一個活動，然后依次選擇與最后選中活動兼容的活動
遞歸版本算法：
- 在已排序的活動列表中，找到第一個與最后選中活動兼容的活動
- 遞歸處理剩余活動
主函數中提供了示例數據，并測試了兩種版本的算法

????????運行上述代碼，會輸出選中的活動索引，兩種方法得到的結果是一致的。這驗證了貪心算法在活動選擇問題上的有效性。

16.2 貪心算法原理

????????貪心算法通過一系列選擇來構造問題的解。在每一步，它選擇在當前看來最好的選項，而不考慮過去的選擇，也不擔心未來的后果。這種 "短視" 的選擇策略在某些問題上能夠得到最優解。

貪心算法的核心要素

要使用貪心算法解決問題，通常需要滿足以下兩個關鍵性質：

貪心選擇性質：全局最優解可以通過一系列局部最優選擇（即貪心選擇）來得到。也就是說，在做出選擇時，我們只需要考慮當前狀態下的最優選擇，而不需要考慮子問題的解。
最優子結構性質：問題的最優解包含其子問題的最優解。如果我們做出了一個貪心選擇，那么剩下的問題可以轉化為一個更小的子問題，而這個子問題的最優解可以與我們的貪心選擇結合，形成原問題的最優解。

貪心算法與動態規劃的對比

貪心算法和動態規劃都用于解決具有最優子結構的問題，但它們的策略不同：

特性	貪心算法	動態規劃
決策方式	每次選擇局部最優，不回溯	自底向上或自頂向下計算，保存子問題解
適用問題	具有貪心選擇性質的問題	所有具有最優子結構的問題
時間復雜度	通常較低（O (n log n) 或 O (n)）	較高（通常為多項式時間）
例子	活動選擇、哈夫曼編碼	最長公共子序列、背包問題

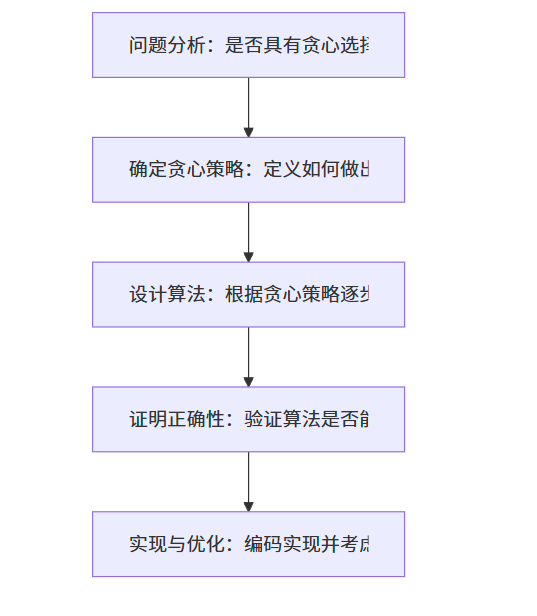
綜合案例：找零問題

????????問題描述：假設貨幣系統有面額為 25、10、5、1 的硬幣，如何用最少的硬幣數找給顧客一定金額的零錢？

貪心策略：每次選擇不超過剩余金額的最大面額硬幣，直到找零完成。

#include <iostream>
#include <vector>
#include <algorithm>using namespace std;/*** 貪心算法解決找零問題* @param denominations 硬幣面額（從大到小排序）* @param amount 需要找零的金額* @return 每種硬幣的使用數量*/
vector<int> makeChange(const vector<int>& denominations, int amount) {vector<int> counts(denominations.size(), 0);int remaining = amount;for (int i = 0; i < denominations.size() && remaining > 0; i++) {// 選擇當前最大面額的硬幣counts[i] = remaining / denominations[i];// 更新剩余金額remaining -= counts[i] * denominations[i];}// 如果還有剩余金額，說明無法用給定面額找零if (remaining > 0) {return {}; // 返回空向量表示無法找零}return counts;
}int main() {// 硬幣面額（從大到小排序）vector<int> denominations = {25, 10, 5, 1};int amount;cout << "請輸入需要找零的金額：";cin >> amount;vector<int> counts = makeChange(denominations, amount);if (counts.empty()) {cout << "無法用給定的硬幣面額完成找零" << endl;} else {cout << "找零 " << amount << " 需要的硬幣數量：" << endl;int total = 0;for (int i = 0; i < denominations.size(); i++) {if (counts[i] > 0) {cout << denominations[i] << "分：" << counts[i] << "枚" << endl;total += counts[i];}}cout << "總共需要：" << total << "枚硬幣" << endl;}return 0;
}

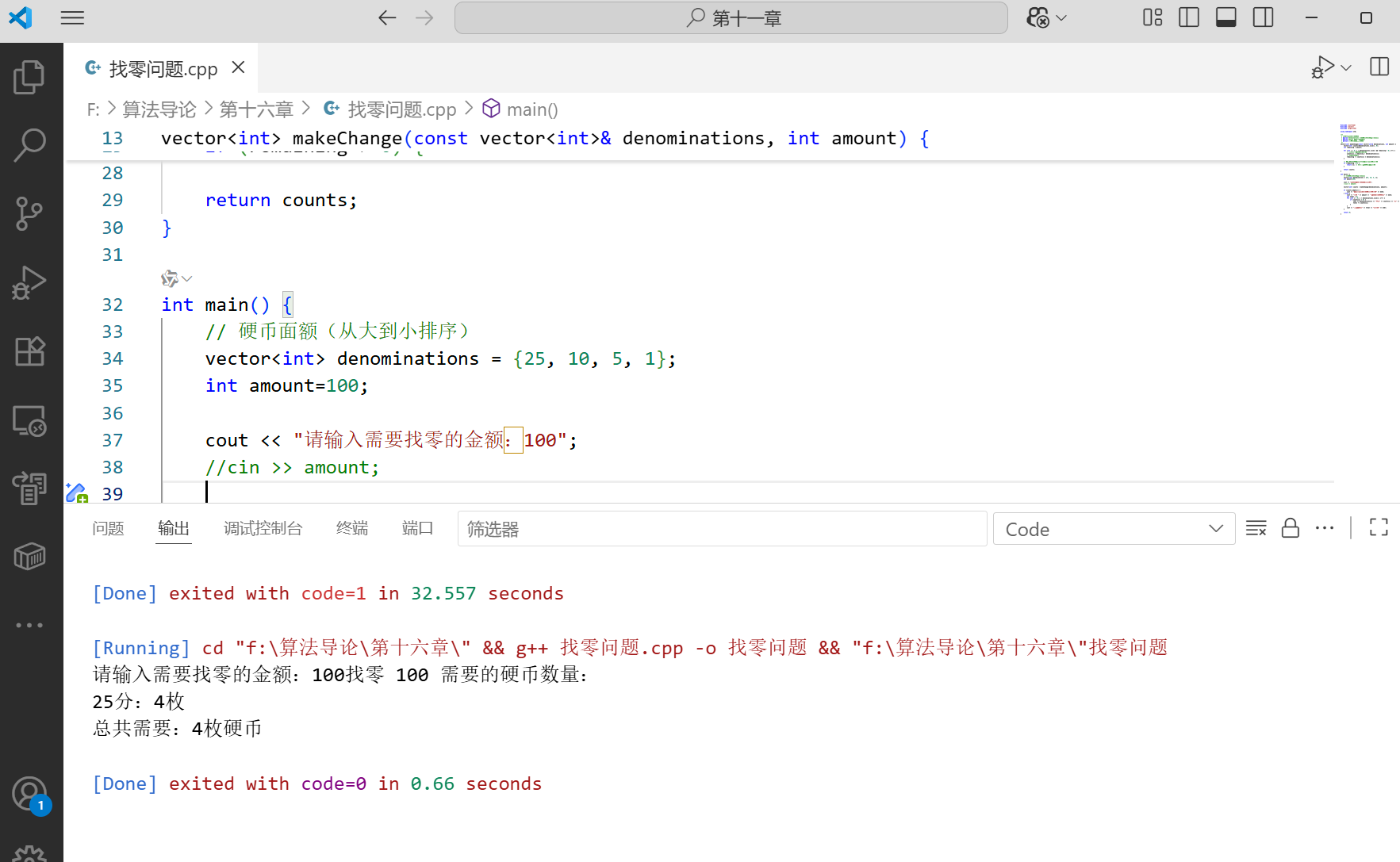
代碼說明：

算法先對硬幣面額從大到小排序（示例中已預先排序）
對于每種面額，計算最多能使用多少枚而不超過剩余金額
更新剩余金額，繼續處理下一面額
如果最終剩余金額為 0，則返回各面額的使用數量；否則表示無法找零

????????注意：貪心算法并非在所有貨幣系統中都能得到最優解。例如，如果貨幣面額為 25、10、1，要找 30 元，貪心算法會選擇 25+1+1+1+1+1（6 枚），但最優解是 10+10+10（3 枚）。因此，貪心算法的適用性取決于問題本身的特性。

16.3 赫夫曼編碼

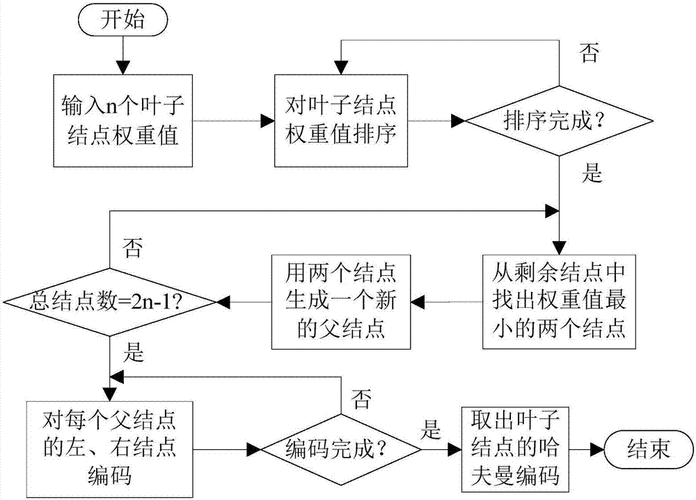
????????赫夫曼編碼（Huffman Coding）是一種用于數據壓縮的貪心算法，由 David A. Huffman 于 1952 年提出。它通過為出現頻率較高的字符分配較短的編碼，為出現頻率較低的字符分配較長的編碼，從而實現數據的高效壓縮。

赫夫曼編碼的基本概念

前綴碼：一種編碼方式，其中任何一個字符的編碼都不是另一個字符編碼的前綴。這種特性使得我們可以無需分隔符就能解碼。
二叉樹表示：赫夫曼編碼通常用二叉樹表示，左分支表示 0，右分支表示 1，樹葉表示字符。
構建過程：基于字符出現的頻率構建赫夫曼樹，頻率高的字符離根節點近（編碼短），頻率低的字符離根節點遠（編碼長）。

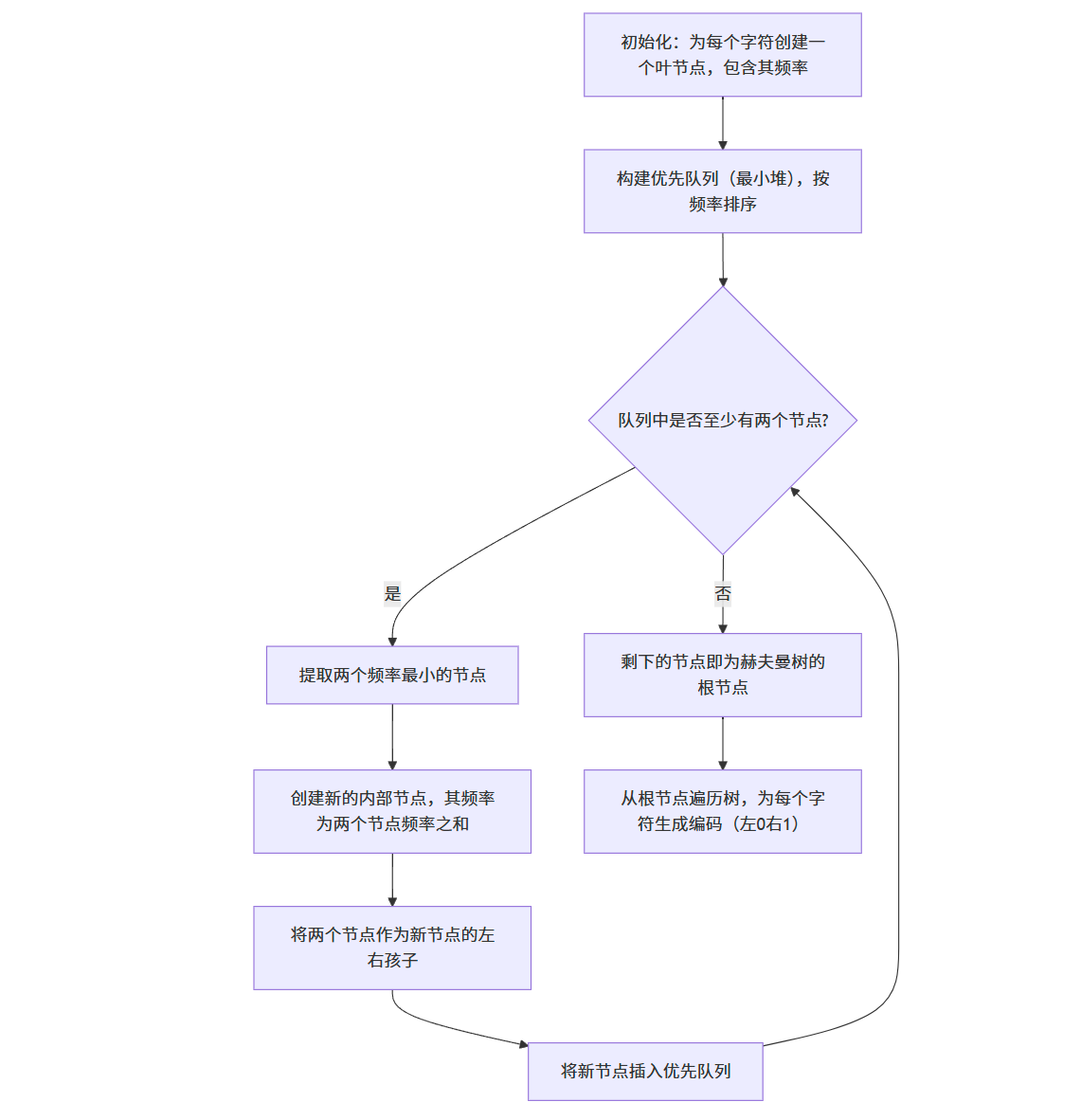
代碼實現

下面是赫夫曼編碼的完整 C++ 實現：

#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
#include <string>
#include <memory>using namespace std;// 赫夫曼樹節點
struct HuffmanNode {char data;           // 字符int freq;            // 頻率shared_ptr<HuffmanNode> left, right; // 左右孩子HuffmanNode(char data, int freq) : data(data), freq(freq), left(nullptr), right(nullptr) {}
};// 優先隊列的比較函數（最小堆）
struct CompareNodes {bool operator()(const shared_ptr<HuffmanNode>& a, const shared_ptr<HuffmanNode>& b) {return a->freq > b->freq; // 頻率小的節點優先級高}
};/*** 構建赫夫曼樹* @param freq 字符頻率映射* @return 赫夫曼樹的根節點*/
shared_ptr<HuffmanNode> buildHuffmanTree(const unordered_map<char, int>& freq) {// 創建優先隊列（最小堆）priority_queue<shared_ptr<HuffmanNode>, vector<shared_ptr<HuffmanNode>>, CompareNodes> pq;// 為每個字符創建葉節點并加入隊列for (const auto& pair : freq) {pq.push(make_shared<HuffmanNode>(pair.first, pair.second));}// 構建赫夫曼樹while (pq.size() > 1) {// 提取兩個頻率最小的節點auto left = pq.top();pq.pop();auto right = pq.top();pq.pop();// 創建新的內部節點auto internal = make_shared<HuffmanNode>('$', left->freq + right->freq);internal->left = left;internal->right = right;// 將新節點加入隊列pq.push(internal);}// 剩下的節點是根節點return pq.top();
}/*** 遞歸生成赫夫曼編碼* @param root 赫夫曼樹的根節點* @param currentCode 當前編碼* @param huffmanCodes 存儲生成的編碼*/
void generateCodes(const shared_ptr<HuffmanNode>& root, string currentCode, unordered_map<char, string>& huffmanCodes) {if (!root) return;// 如果是葉節點，保存編碼if (root->data != '$') {huffmanCodes[root->data] = currentCode.empty() ? "0" : currentCode;return;}// 遞歸處理左右子樹generateCodes(root->left, currentCode + "0", huffmanCodes);generateCodes(root->right, currentCode + "1", huffmanCodes);
}/*** 編碼字符串* @param str 原始字符串* @param huffmanCodes 赫夫曼編碼映射* @return 編碼后的二進制字符串*/
string encodeString(const string& str, const unordered_map<char, string>& huffmanCodes) {string encoded;for (char c : str) {encoded += huffmanCodes.at(c);}return encoded;
}/*** 解碼二進制字符串* @param encoded 編碼后的二進制字符串* @param root 赫夫曼樹的根節點* @return 解碼后的原始字符串*/
string decodeString(const string& encoded, const shared_ptr<HuffmanNode>& root) {string decoded;auto current = root;for (char bit : encoded) {if (bit == '0') {current = current->left;} else {current = current->right;}// 如果到達葉節點，添加字符并重置當前節點if (!current->left && !current->right) {decoded += current->data;current = root;}}return decoded;
}/*** 計算字符頻率* @param str 輸入字符串* @return 字符頻率映射*/
unordered_map<char, int> calculateFrequency(const string& str) {unordered_map<char, int> freq;for (char c : str) {freq[c]++;}return freq;
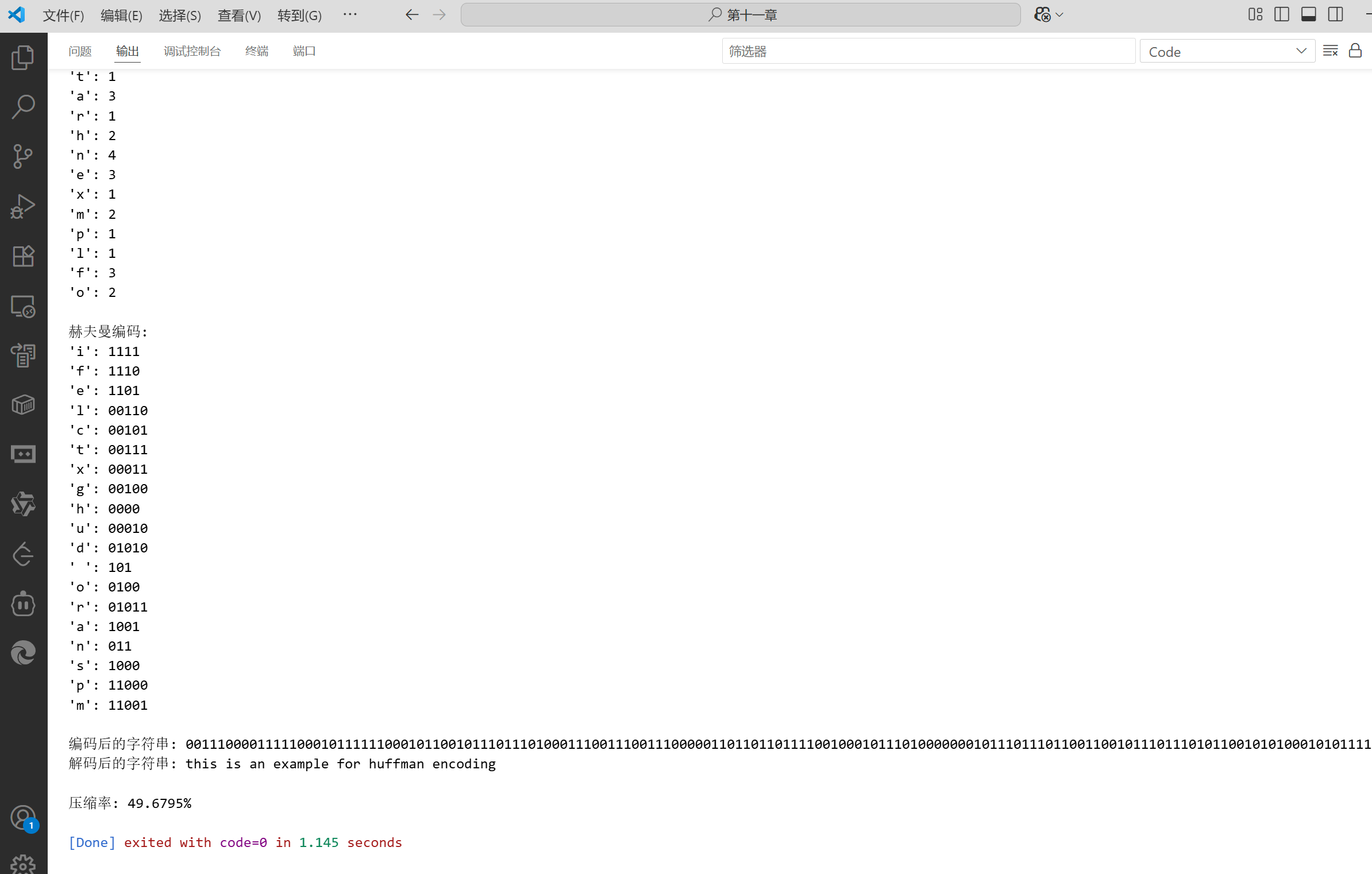
}int main() {string str = "this is an example for huffman encoding";cout << "原始字符串: " << str << endl;// 計算字符頻率auto freq = calculateFrequency(str);cout << "\n字符頻率:" << endl;for (const auto& pair : freq) {cout << "'" << pair.first << "': " << pair.second << endl;}// 構建赫夫曼樹auto root = buildHuffmanTree(freq);// 生成赫夫曼編碼unordered_map<char, string> huffmanCodes;generateCodes(root, "", huffmanCodes);cout << "\n赫夫曼編碼:" << endl;for (const auto& pair : huffmanCodes) {cout << "'" << pair.first << "': " << pair.second << endl;}// 編碼字符串string encoded = encodeString(str, huffmanCodes);cout << "\n編碼后的字符串: " << encoded << endl;// 解碼字符串string decoded = decodeString(encoded, root);cout << "解碼后的字符串: " << decoded << endl;// 計算壓縮率double originalSize = str.size() * 8; // 假設每個字符8位double compressedSize = encoded.size();double compressionRatio = 100 - (compressedSize / originalSize * 100);cout << "\n壓縮率: " << compressionRatio << "%" << endl;return 0;
}

代碼說明

HuffmanNode 結構體：表示赫夫曼樹的節點，包含字符、頻率和左右孩子指針
構建赫夫曼樹：
- 使用優先隊列（最小堆）存儲節點
- 反復提取兩個頻率最小的節點，創建新的內部節點，直到只剩下一個節點（根節點）
生成編碼：通過遞歸遍歷赫夫曼樹，為每個字符生成二進制編碼（左 0 右 1）
編碼與解碼：
- 編碼：將原始字符串轉換為二進制編碼字符串
- 解碼：將二進制編碼字符串還原為原始字符串
輔助功能：計算字符頻率、計算壓縮率等

????????運行上述代碼，可以看到赫夫曼編碼如何為頻率高的字符分配較短的編碼，從而實現數據壓縮。

16.4 擬陣和貪心算法

????????擬陣（Matroid）是一種組合結構，它為我們提供了一個理解貪心算法有效性的通用框架。許多可以用貪心算法解決的問題都可以建模為擬陣上的優化問題。

代碼實現（基于擬陣的活動選擇）

我們可以用擬陣理論來重新實現活動選擇問題，展示擬陣與貪心算法的關系：

#include <iostream>
#include <vector>
#include <algorithm>
#include <unordered_set>using namespace std;// 活動結構體
struct Activity {int start;int finish;int index;int weight; // 活動權重，用于加權活動選擇問題
};// 按權重降序排序
bool compareWeight(const Activity& a, const Activity& b) {return a.weight > b.weight;
}// 檢查活動集是否獨立（即是否存在沖突）
bool isIndependent(const vector<Activity>& activities, const unordered_set<int>& selectedIndices) {vector<Activity> selected;for (int idx : selectedIndices) {selected.push_back(activities[idx]);}// 檢查所有選中的活動是否兩兩不沖突for (int i = 0; i < selected.size(); i++) {for (int j = i + 1; j < selected.size(); j++) {// 如果兩個活動時間重疊，則不獨立if (!(selected[i].finish <= selected[j].start || selected[j].finish <= selected[i].start)) {return false;}}}return true;
}/*** 基于擬陣的貪心算法解決加權活動選擇問題* @param activities 活動列表* @return 選中的活動索引集合*/
unordered_set<int> maxWeightIndependentSet(vector<Activity>& activities) {// 按權重降序排序sort(activities.begin(), activities.end(), compareWeight);unordered_set<int> selected;// 依次考慮每個活動for (int i = 0; i < activities.size(); i++) {// 嘗試加入當前活動selected.insert(i);// 檢查是否保持獨立性if (!isIndependent(activities, selected)) {// 如果不獨立，移除該活動selected.erase(i);}}return selected;
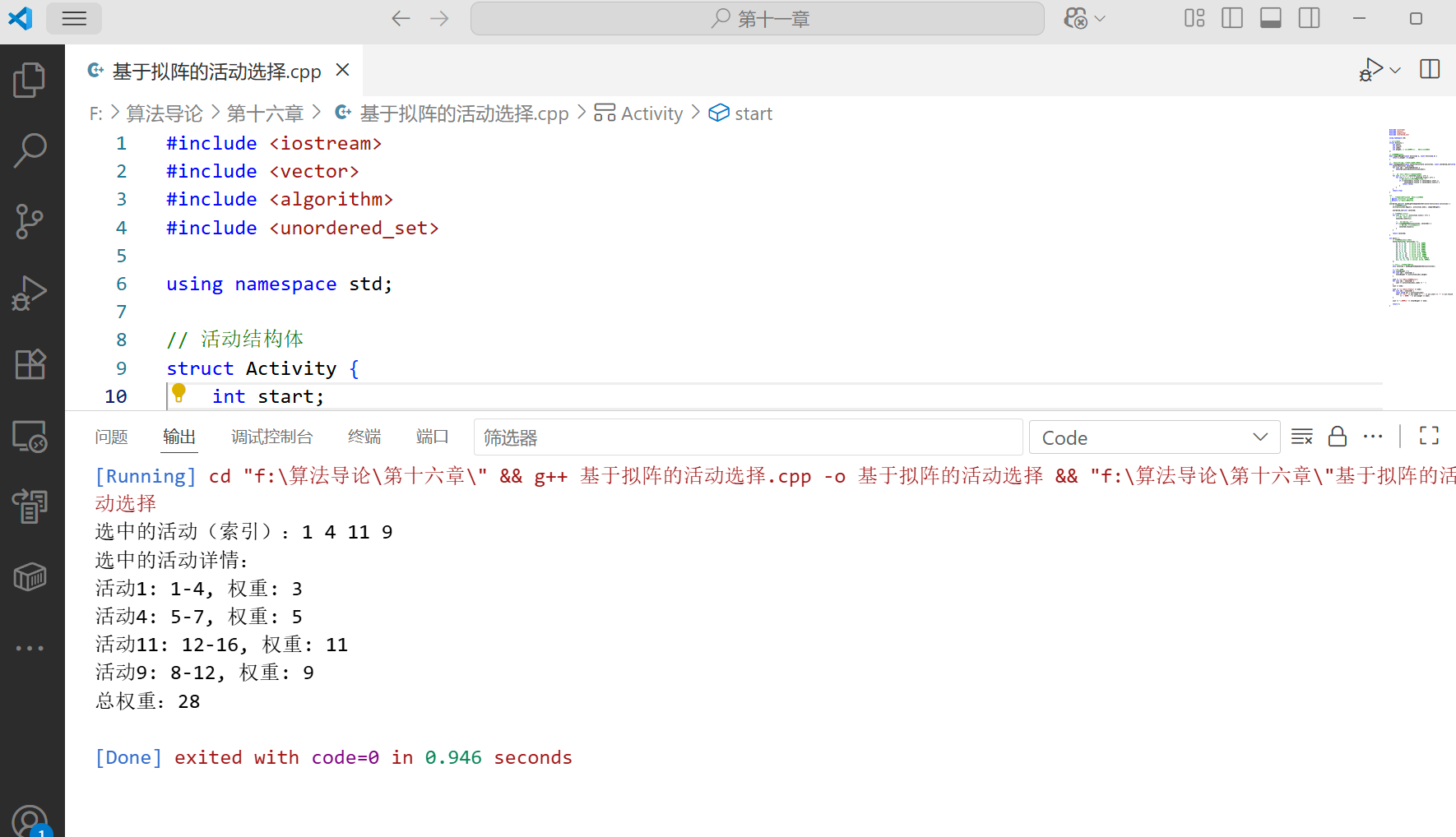
}int main() {// 帶權重的示例活動數據vector<Activity> activities = {{1, 4, 1, 3},   // 活動1: 1-4, 權重3{3, 5, 2, 2},   // 活動2: 3-5, 權重2{0, 6, 3, 4},   // 活動3: 0-6, 權重4{5, 7, 4, 5},   // 活動4: 5-7, 權重5{3, 9, 5, 1},   // 活動5: 3-9, 權重1{5, 9, 6, 6},   // 活動6: 5-9, 權重6{6, 10, 7, 7},  // 活動7: 6-10, 權重7{8, 11, 8, 8},  // 活動8: 8-11, 權重8{8, 12, 9, 9},  // 活動9: 8-12, 權重9{2, 14, 10, 10}, // 活動10: 2-14, 權重10{12, 16, 11, 11} // 活動11: 12-16, 權重11};// 應用基于擬陣的貪心算法auto selected = maxWeightIndependentSet(activities);// 計算總權重int totalWeight = 0;for (int idx : selected) {totalWeight += activities[idx].weight;}cout << "選中的活動（索引）：";for (int idx : selected) {cout << activities[idx].index << " ";}cout << endl;cout << "選中的活動詳情：" << endl;for (int idx : selected) {const auto& act = activities[idx];cout << "活動" << act.index << ": " << act.start << "-" << act.finish << ", 權重: " << act.weight << endl;}cout << "總權重：" << totalWeight << endl;return 0;
}

代碼說明

這個例子實現了加權活動選擇問題，與 16.1 節的問題不同，這里每個活動都有一個權重，我們的目標是選擇總權重最大的兼容活動集。
我們將這個問題建模為擬陣問題：
- 集合?S?是所有活動的集合
- 獨立集?\(\mathcal{I}\)?是所有不沖突的活動子集（即任意兩個活動時間不重疊）
算法步驟：
- 將活動按權重降序排序
- 依次考慮每個活動，如果加入后仍保持獨立性（即與已選活動不沖突），則選中該活動
- 最終得到的集合是總權重最大的獨立集
isIndependent函數用于檢查一個活動集合是否是獨立集（即不包含沖突的活動）

????????這個例子展示了擬陣理論如何為貪心算法提供理論基礎，以及如何將實際問題建模為擬陣上的優化問題。

16.5 用擬陣求解任務調度問題

????????任務調度是計算機科學中的一個重要問題，我們可以利用擬陣理論和貪心算法來求解某些類型的任務調度問題。

問題描述

考慮一個單處理器的任務調度問題：

代碼實現

#include <iostream>
#include <vector>
#include <algorithm>
#include <unordered_set>using namespace std;// 任務結構體
struct Task {int id;         // 任務IDint t;          // 處理時間int w;          // 權重int d;          // 截止時間
};// 按權重/處理時間比值降序排序
bool compareRatio(const Task& a, const Task& b) {// 避免浮點數運算，使用交叉相乘比較return (long long)a.w * b.t > (long long)b.w * a.t;
}// 按截止時間升序排序
bool compareDeadline(const Task& a, const Task& b) {return a.d < b.d;
}/*** 檢查任務集是否可以被可行調度* @param tasks 要檢查的任務集* @return 如果可以被可行調度，返回true；否則返回false*/
bool isFeasible(vector<Task> tasks) {// 按截止時間升序排序sort(tasks.begin(), tasks.end(), compareDeadline);int totalTime = 0;for (const auto& task : tasks) {totalTime += task.t;// 檢查前綴和是否超過當前任務的截止時間if (totalTime > task.d) {return false;}}return true;
}/*** 用擬陣和貪心算法求解任務調度問題* @param tasks 所有任務的列表* @return 選中的任務集合*/
vector<Task> scheduleTasks(vector<Task>& tasks) {// 按權重/處理時間比值降序排序sort(tasks.begin(), tasks.end(), compareRatio);vector<Task> selected;// 依次考慮每個任務for (const auto& task : tasks) {// 嘗試加入當前任務selected.push_back(task);// 檢查是否仍能可行調度if (!isFeasible(selected)) {// 如果不可行，移除該任務selected.pop_back();}}return selected;
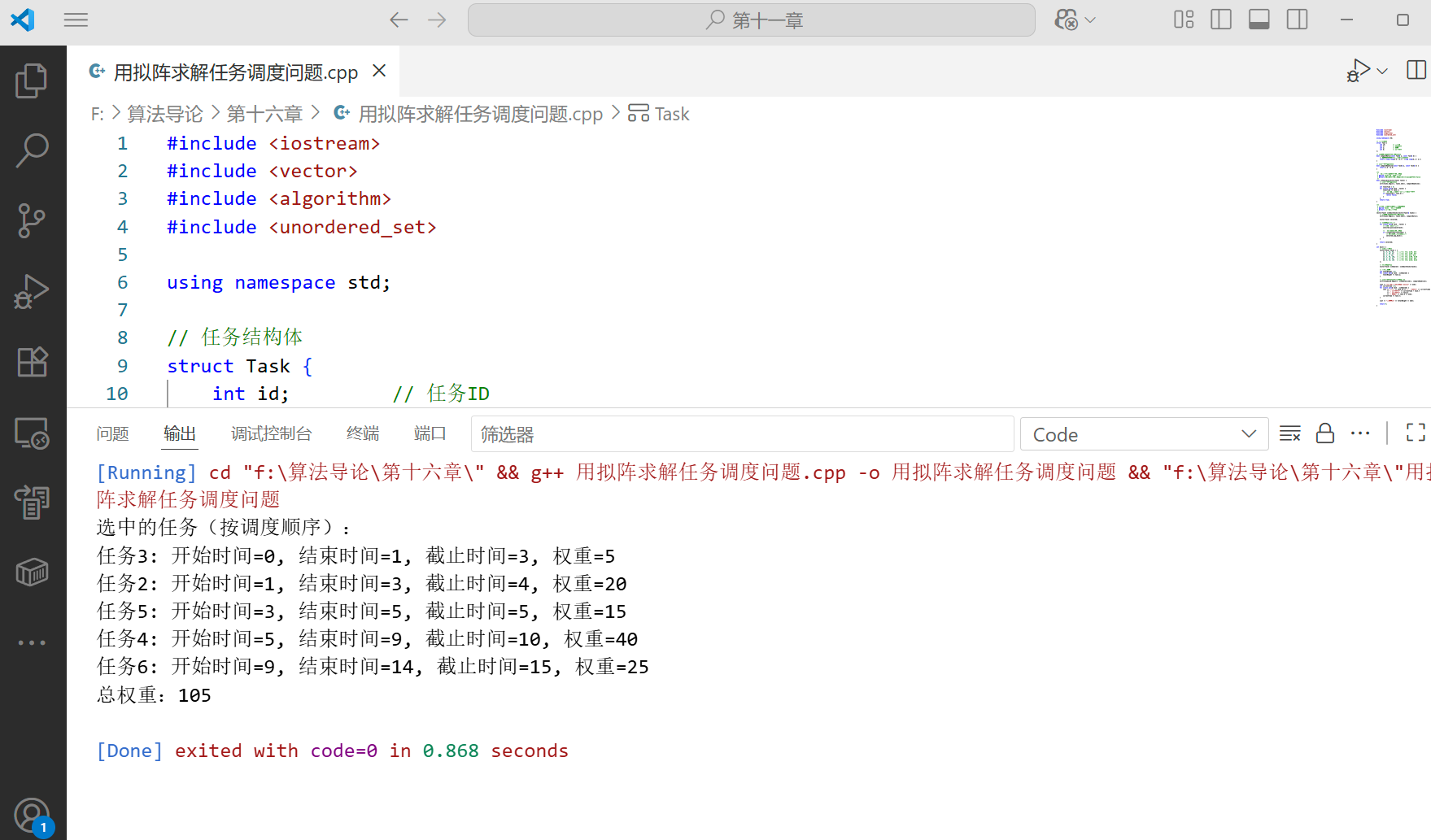
}int main() {// 示例任務數據vector<Task> tasks = {{1, 3, 10, 6},   // 任務1: t=3, w=10, d=6{2, 2, 20, 4},   // 任務2: t=2, w=20, d=4{3, 1, 5, 3},    // 任務3: t=1, w=5, d=3{4, 4, 40, 10},  // 任務4: t=4, w=40, d=10{5, 2, 15, 5},   // 任務5: t=2, w=15, d=5{6, 5, 25, 15}   // 任務6: t=5, w=25, d=15};// 應用調度算法vector<Task> scheduled = scheduleTasks(tasks);// 計算總權重int totalWeight = 0;for (const auto& task : scheduled) {totalWeight += task.w;}// 按截止時間排序以顯示調度順序sort(scheduled.begin(), scheduled.end(), compareDeadline);cout << "選中的任務（按調度順序）：" << endl;int currentTime = 0;for (const auto& task : scheduled) {cout << "任務" << task.id << ": 開始時間=" << currentTime << ", 結束時間=" << currentTime + task.t << ", 截止時間=" << task.d << ", 權重=" << task.w << endl;currentTime += task.t;}cout << "總權重：" << totalWeight << endl;return 0;
}

代碼說明

這個實現解決了帶截止時間和權重的單處理器任務調度問題，目標是最大化總權重同時滿足所有截止時間約束。
算法核心步驟：
- 按權重 / 處理時間比值降序排序任務（優先考慮 "單位時間價值" 高的任務）
- 依次嘗試添加任務，每次添加后檢查是否仍能找到可行的調度方案
- 可行調度檢查：按截止時間排序任務，確保所有前綴和（累計處理時間）不超過對應任務的截止時間
最終輸出的是按截止時間排序的任務，這代表了一種可行的調度順序。

????????這個例子展示了如何將實際問題建模為擬陣問題，并應用貪心算法求解，體現了擬陣理論在貪心算法中的基礎作用。

思考題

活動選擇問題中，如果活動有不同的權重，我們希望選擇總權重最大的兼容活動集，此時 16.1 節的貪心算法是否仍然適用？為什么？
證明赫夫曼編碼產生的是最優前綴碼。
考慮 0-1 背包問題：有 n 個物品，每個物品有重量 w_i 和價值 v_i，背包容量為 W，如何選擇物品使得總價值最大且總重量不超過 W。為什么貪心算法（如按價值 / 重量比排序）不能保證得到最優解？這個問題是否可以建模為擬陣問題？
設計一個基于貪心算法的算法，用于求解區間圖的最小頂點覆蓋問題。
考慮一個有向圖的最短路徑問題，從源點到其他所有頂點的最短路徑。Dijkstra 算法是一種貪心算法，它的貪心策略是什么？為什么在存在負權邊的情況下 Dijkstra 算法可能失效？