MATLAB核心技巧：從入門到精通

一

1.數值顯示格式

format style 設置

eg: pi format longE;

2.清除指令

clc 清除命令行窗口

clear 清除工作區

cls

3.搜索路徑設置

path(path,'E:\ads\')

addpath

4.M文件

用戶把要實現的命令寫在一個以.m為擴展的文件中，然后由matlab系統進行解讀，最后運行結果。

類型：

腳本：也可以自己寫函數；

函數：函數名和文件名相同；

5.通用描述

general 命令

函數：rand(), sin(60)

工具箱

abs , sqrt, exp

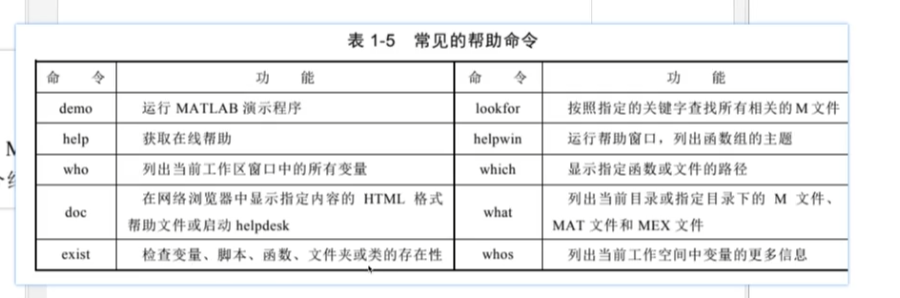
help abs

分號；，不打印在命令行中

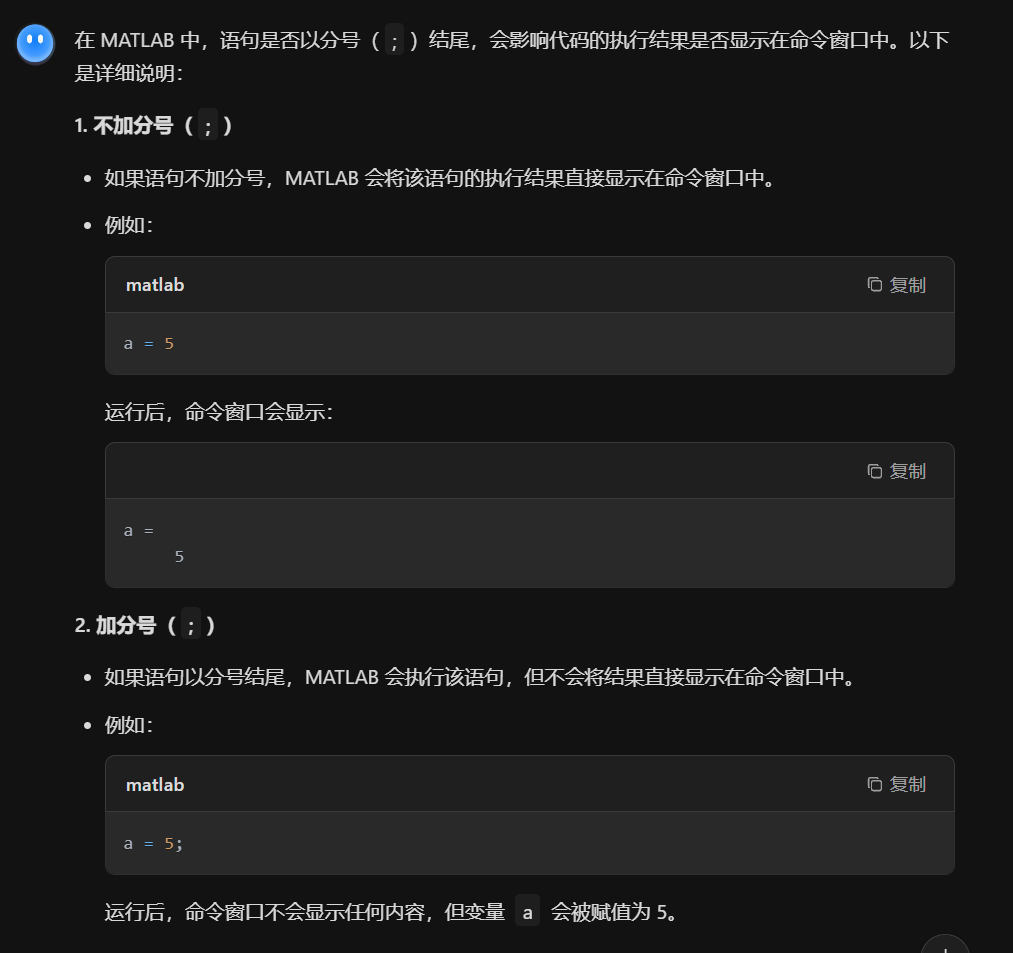
6.通用命令

常用：cls clf clear exit quit home echo type more cd dir load diary pack hold（圖形保持

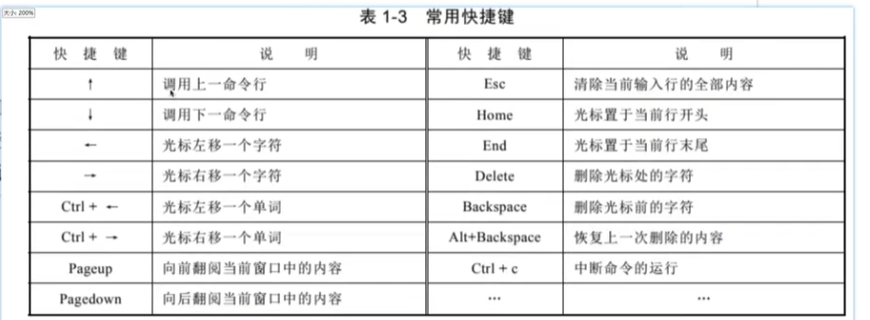
快捷鍵

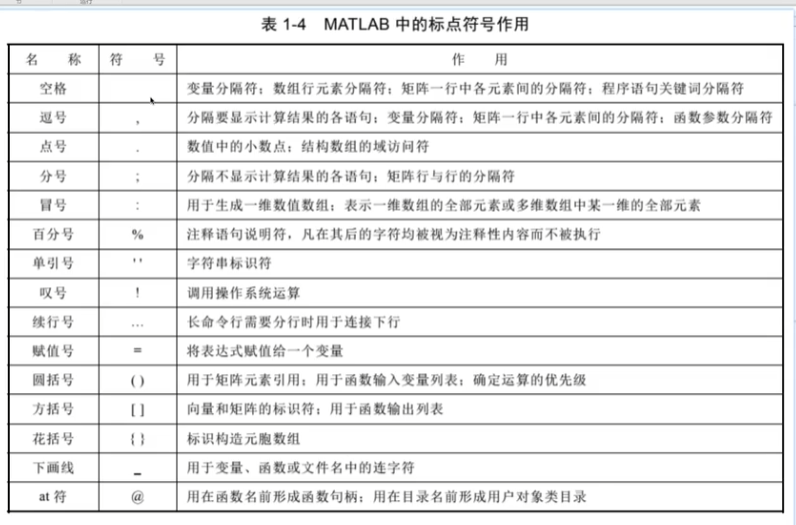
[]向量和矩陣標識符

二

1.向量

冒號表示

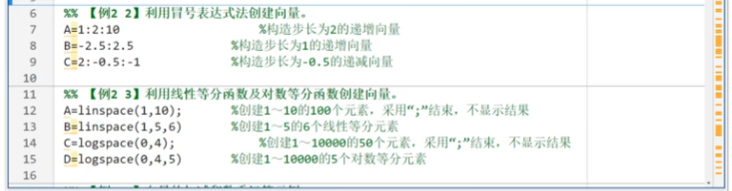
linspace(a1,an,n) n默認100 ，首元素尾元素等分間距

logspace(a1,an,n) n默認50

算數運算

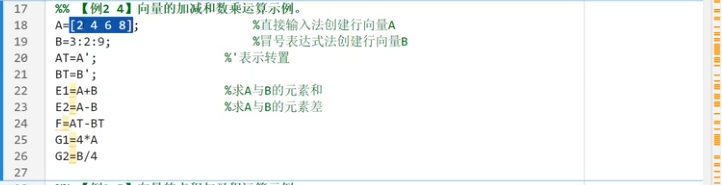
點積和叉積

2.矩陣matrix

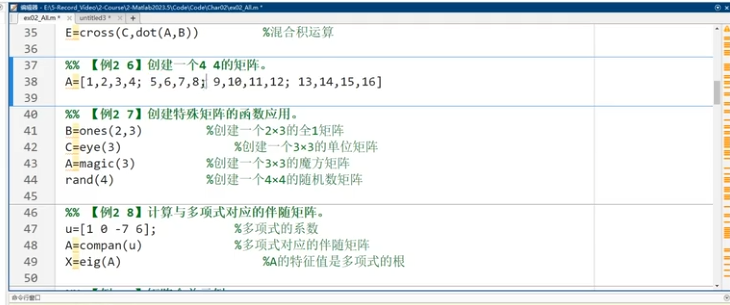
特殊矩陣

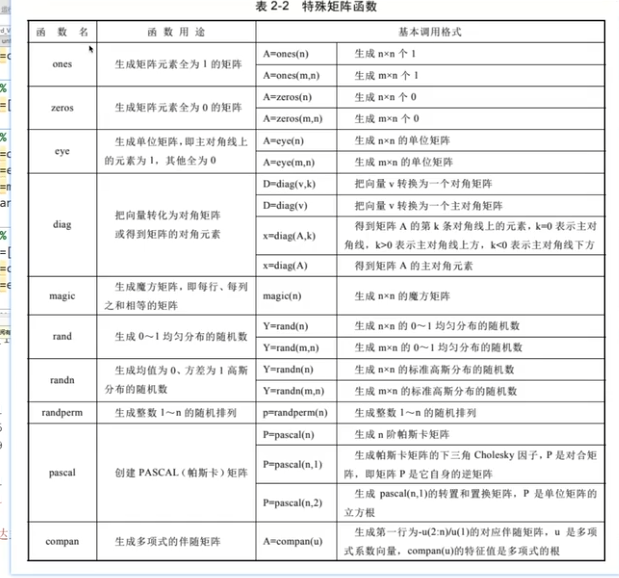
ones(3,3) or ones(3)

zeros( )

eye()

diag()對角

magic

rand 0-1均勻分布

randn 高斯分布

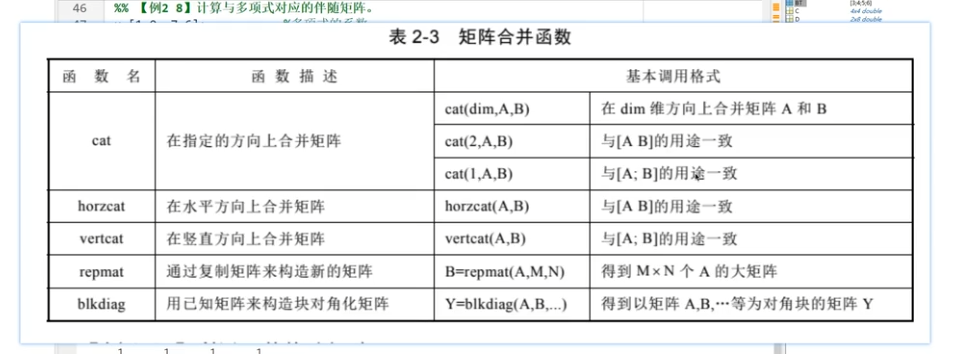
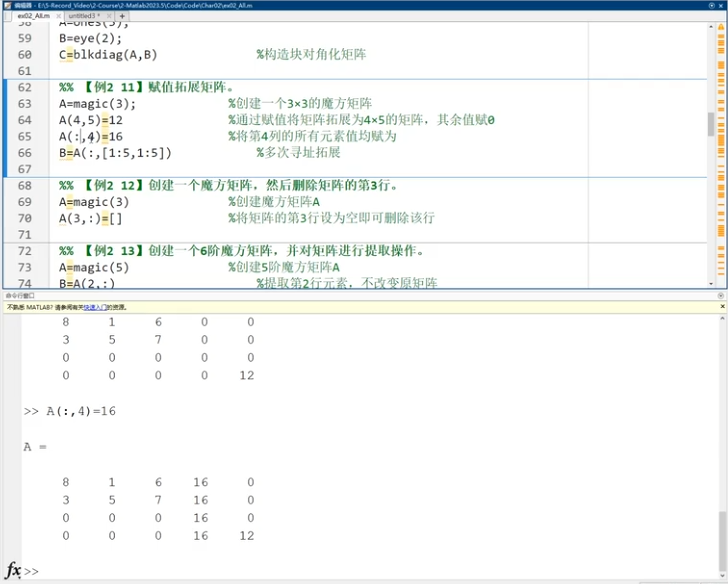
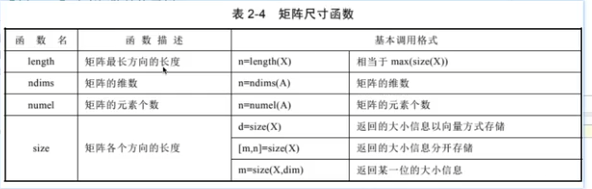
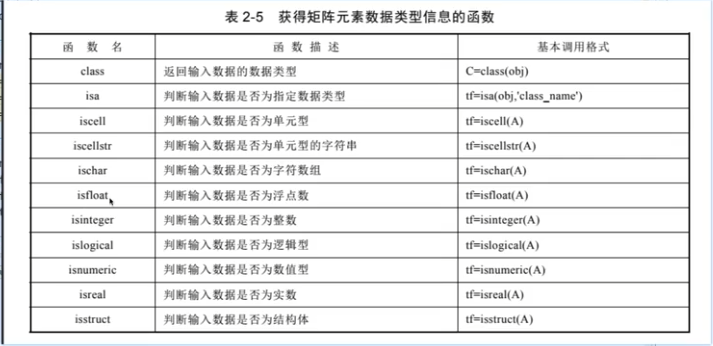
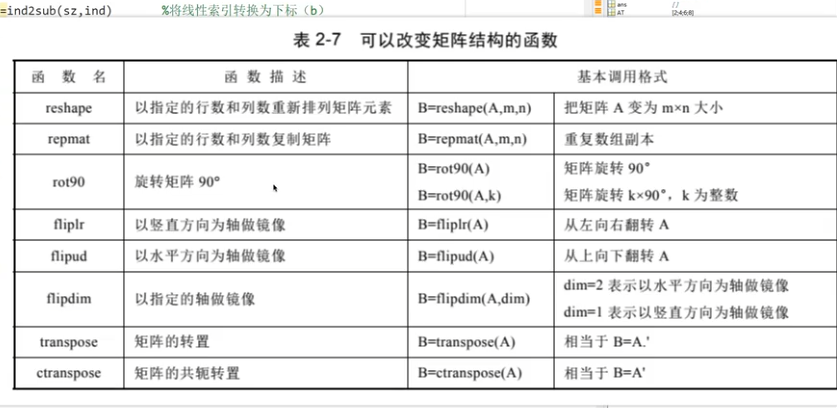
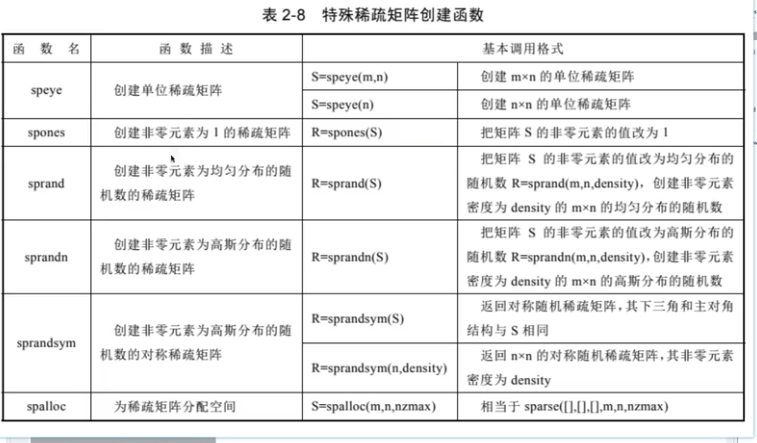
稀疏矩陣

非零元素和行列索引來存，節省空間；

密度：

轉換函數：滿矩陣-稀疏矩陣

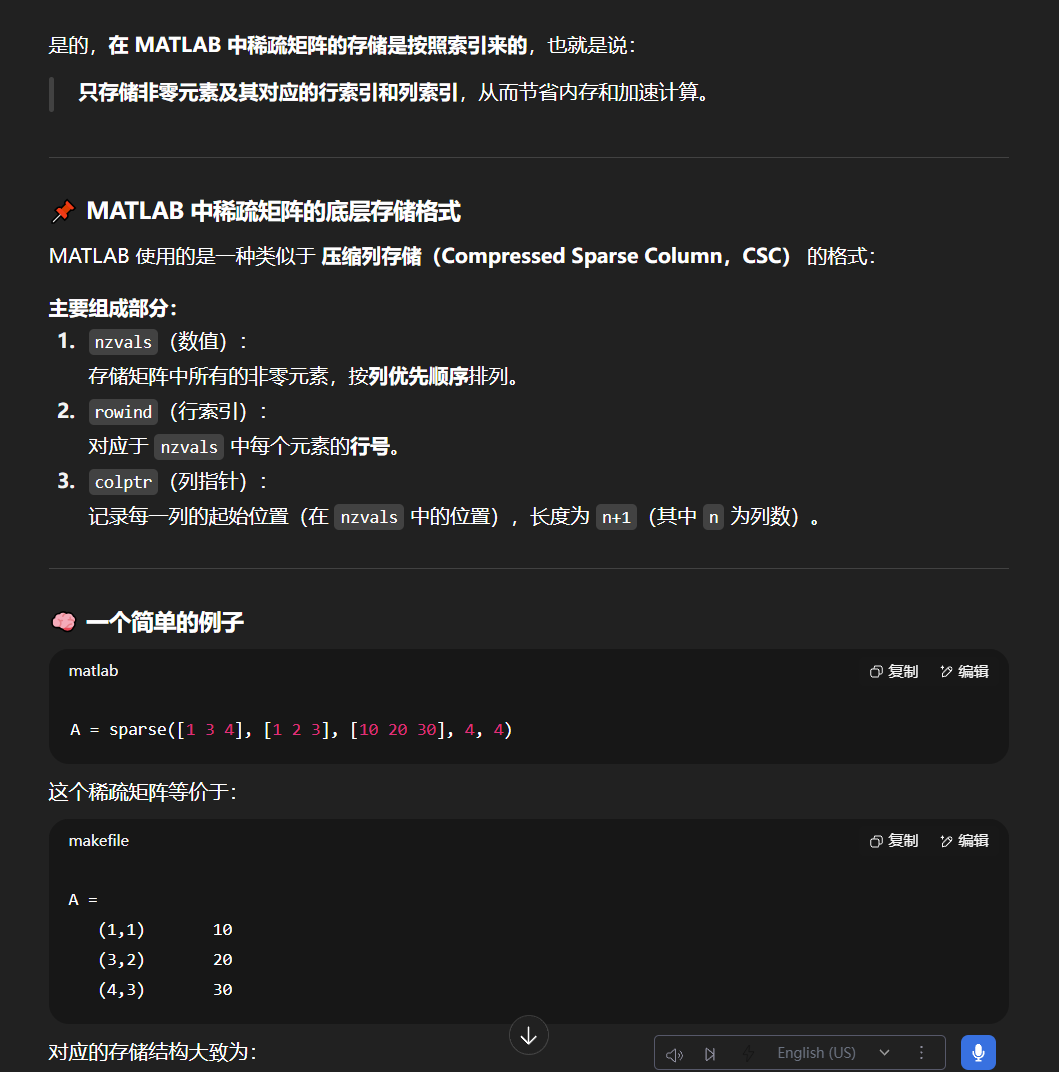
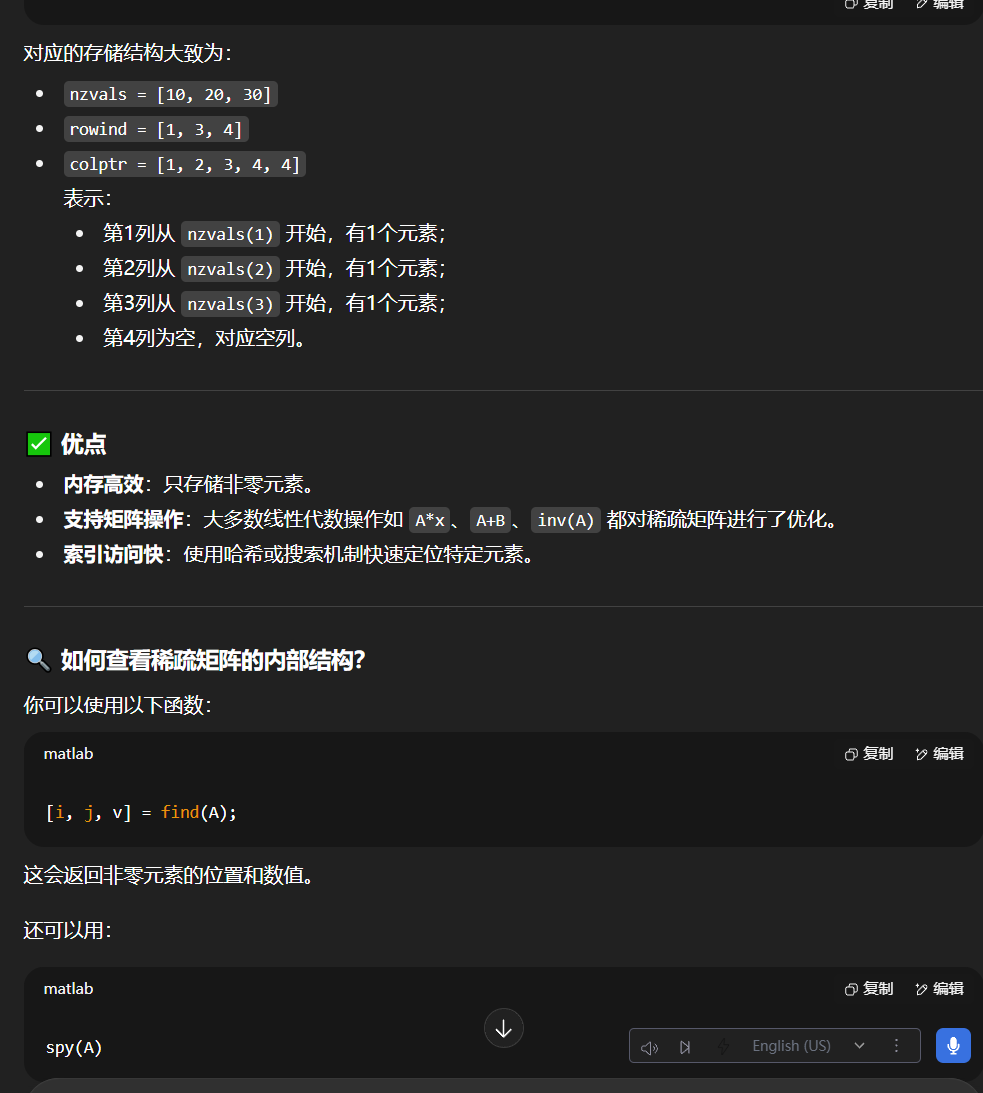
結論

MATLAB 的稀疏矩陣是按索引存儲的，采用的是列優先順序下的壓縮列存儲（CSC）格式。只保存了非零元素及其所在的行列索引，從而實現了高效的內存利用和運算性能。

導入外部數據 load

多維數組

三

1.數據類型

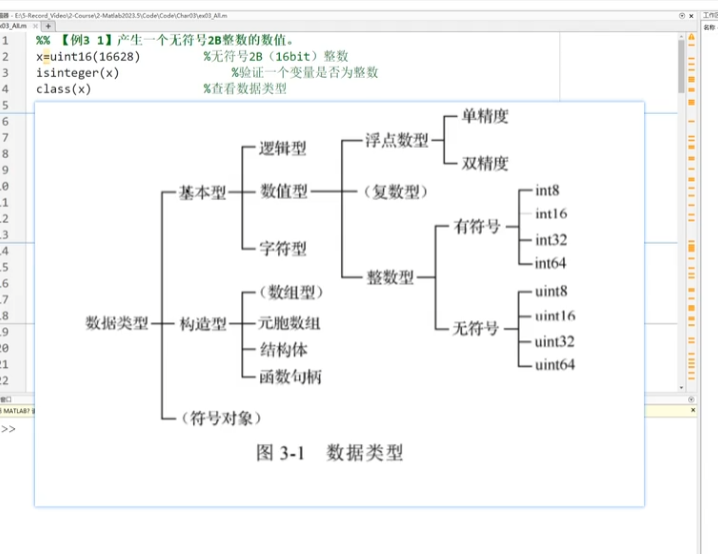
isinteger(x)

class(x)

雙精度浮點（默認）

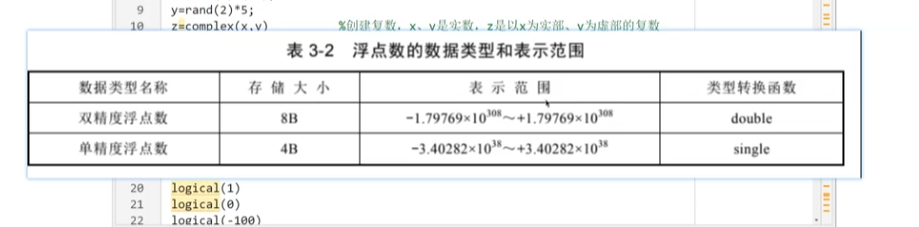
2.類型轉換函數

復數：z = complex(x,y)

? ? ? ? ? ?z = complex(x)

? ? ? ? ? ?z = 12 + 6i;

? ? ? ? ? ?z = rand(2)*2

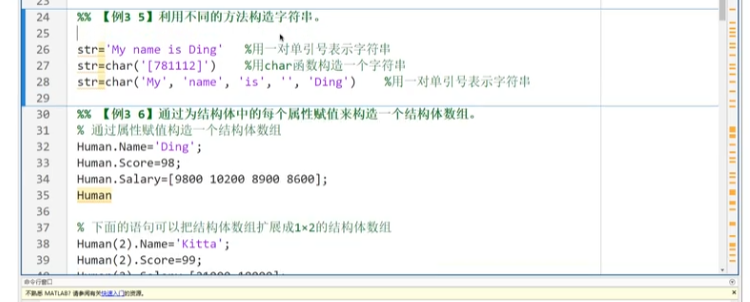
3.字符，結構體（C++）

?4.元胞數組

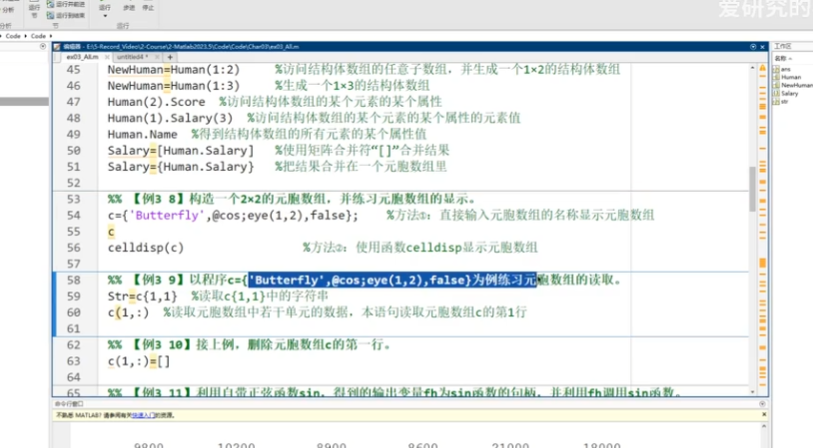
5.函數句柄

可作為參數傳遞給其他函數，C++中有相同概念函數指針或回調函數，執行時機和邏輯分離；

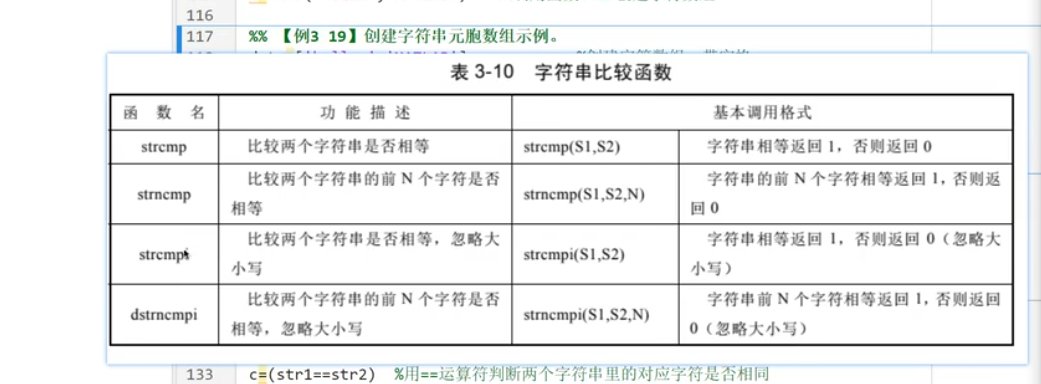
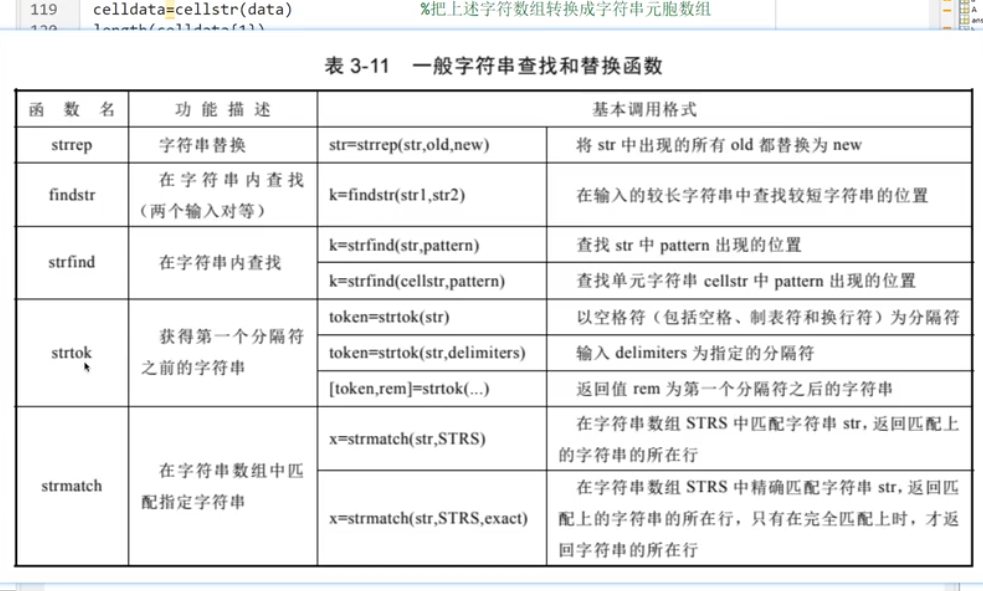
6.字符串

四

1.程序

M文件，擴展名.m。通過編寫M文件可以實現各種復雜運算。

eg:

循環語句：for and while 前者有次數，后者沒有，通過條件判斷式來決定

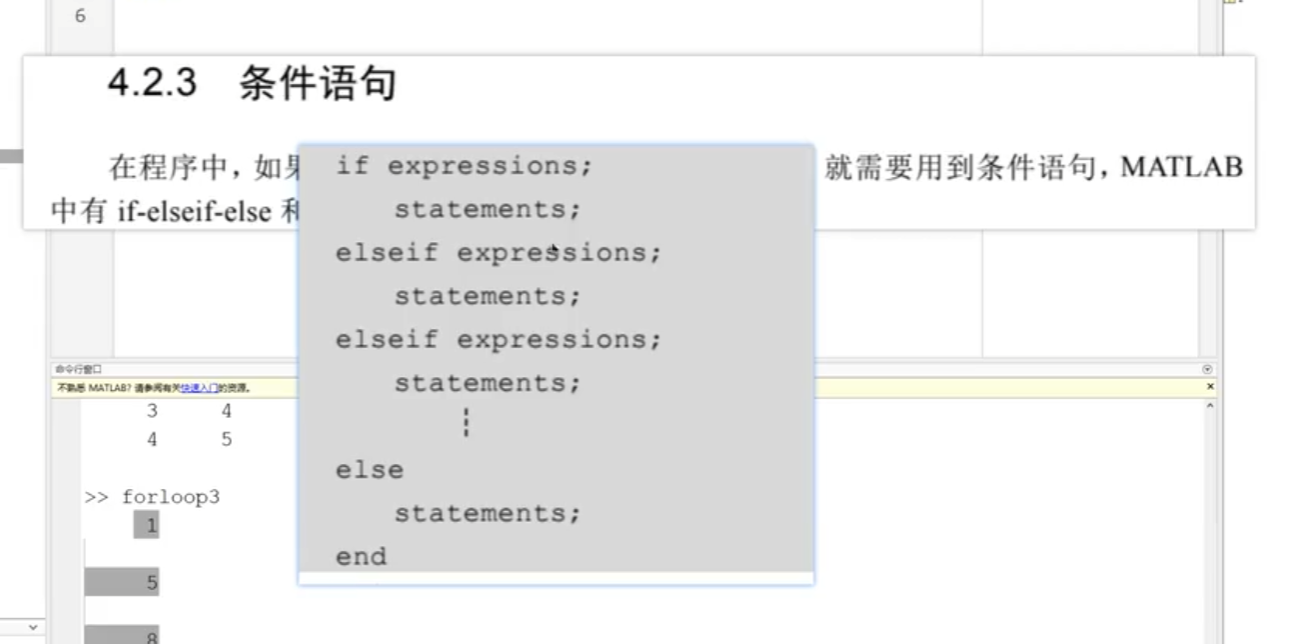
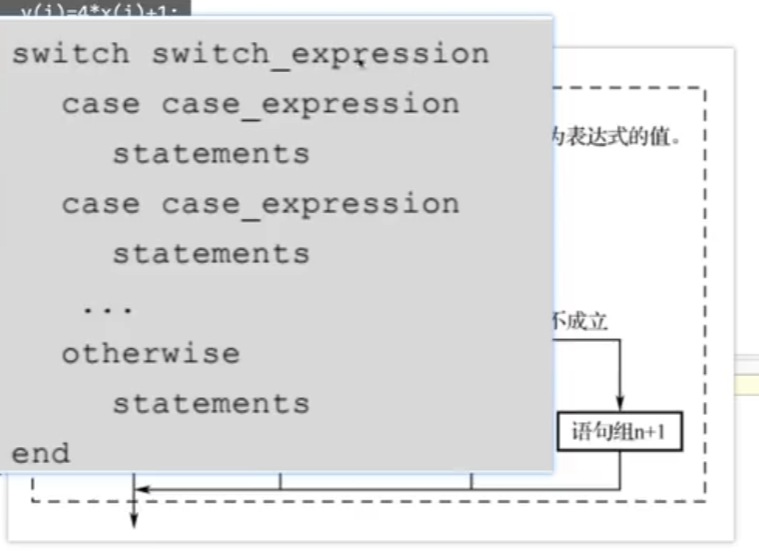
條件語句：ifelse switch case

continue?

return?

break

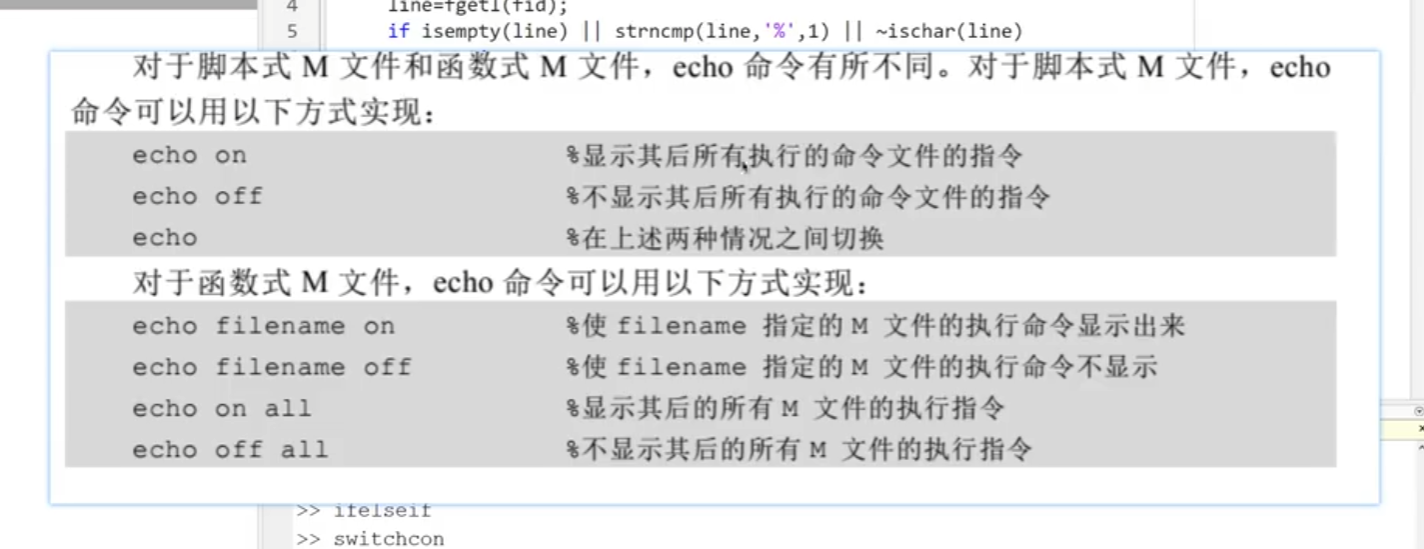
交互命令：

echo

error

keyboard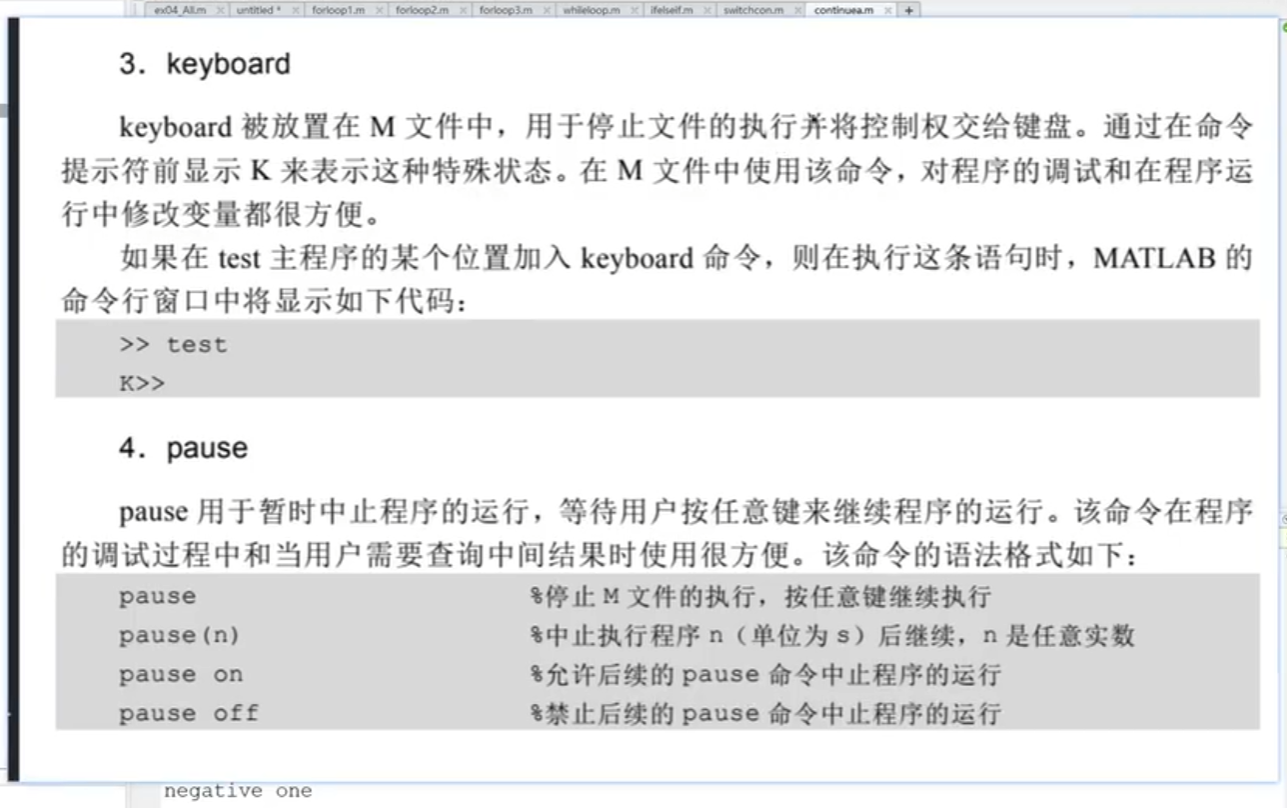

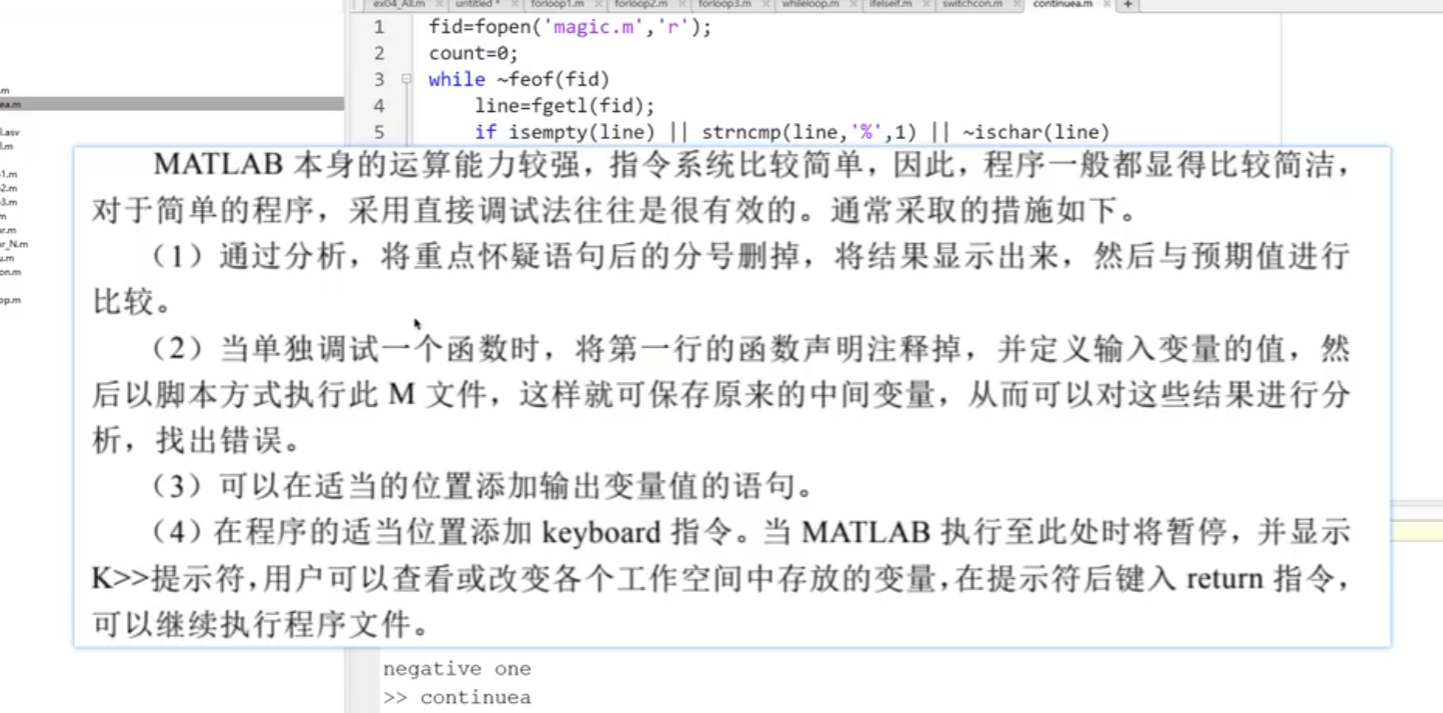
2.調試

五

矩陣運算

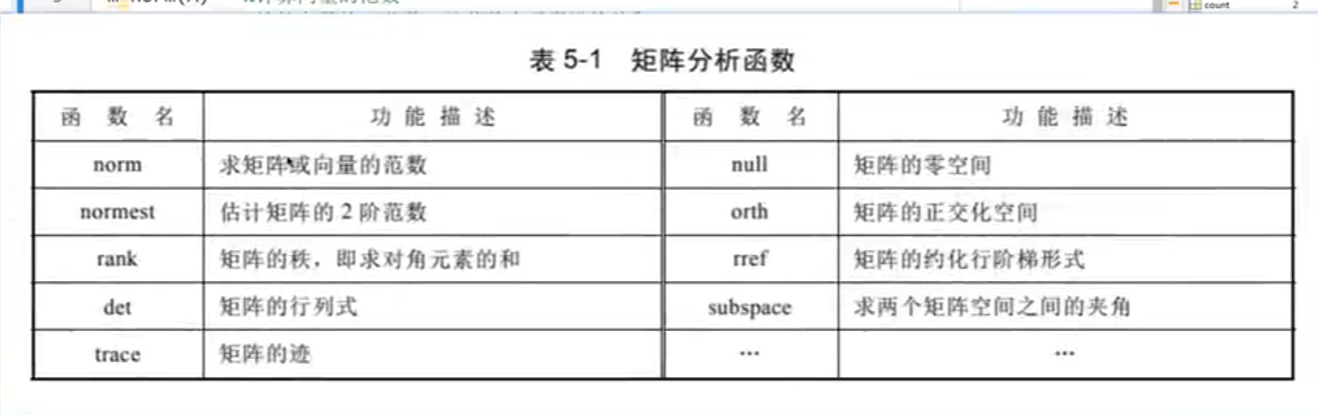
范數

det?

cond判斷奇異性

rank

trace

特征值和特征向量

矩陣空間夾角

矩陣分解

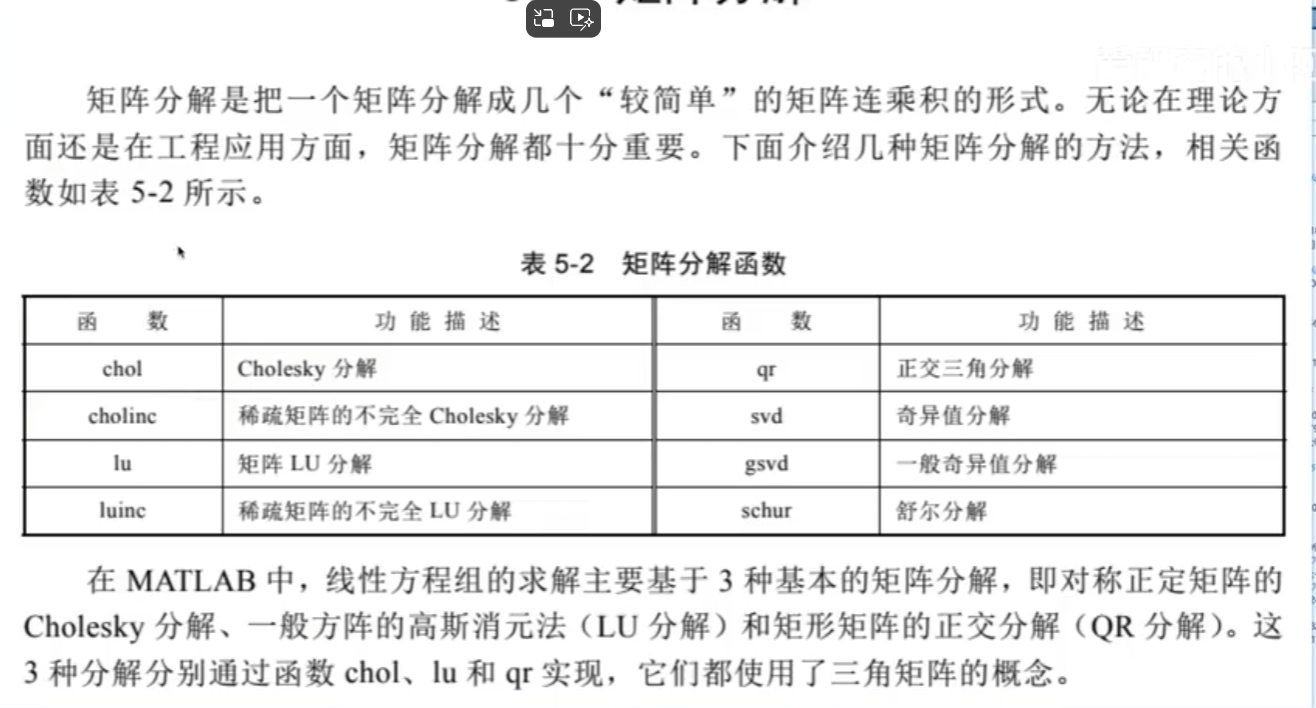
1.chol

2.LU

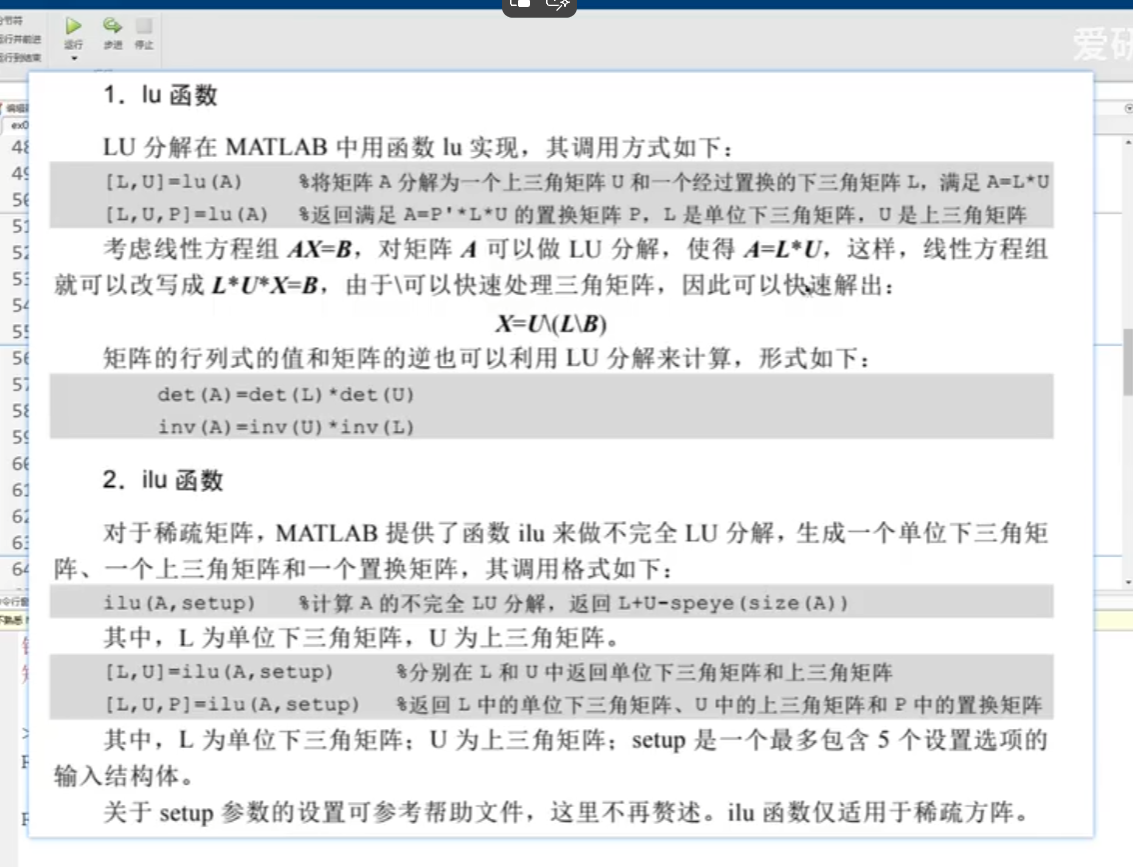
3.QR

4.左右除：

為了方便記憶對哪個矩陣進行逆運算，規律如下：
? ? ? ? 在可逆形式下轉換成逆矩陣，右除對右邊矩陣逆，左除對左邊矩陣逆。
? ? ? ? 1. ? ? C/B=C*(inv(B)) ?(C右除B等于C乘以B的逆）
? ? ? ? 2. ? ? A\C=inv(A)*C （A左除C=A的逆乘以C）

六

1.可視化

eg:

步驟：

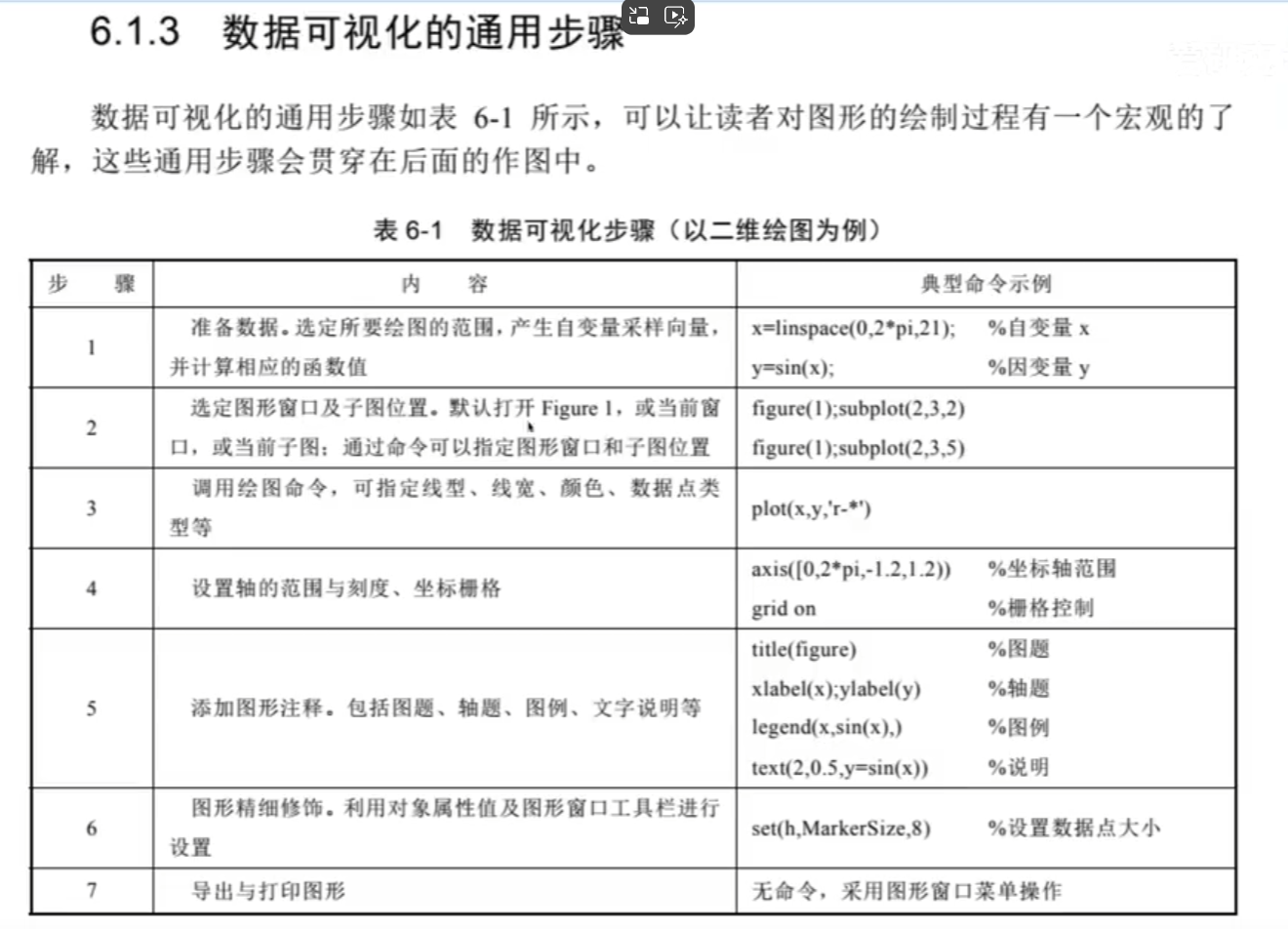
2.二維圖形繪制

雙坐標軸

hold on 疊圖

hold off

子圖

subplot(m,n,k)

3.三維圖形

plot3

mesh 三維網格圖

surf

3.二維特殊圖形

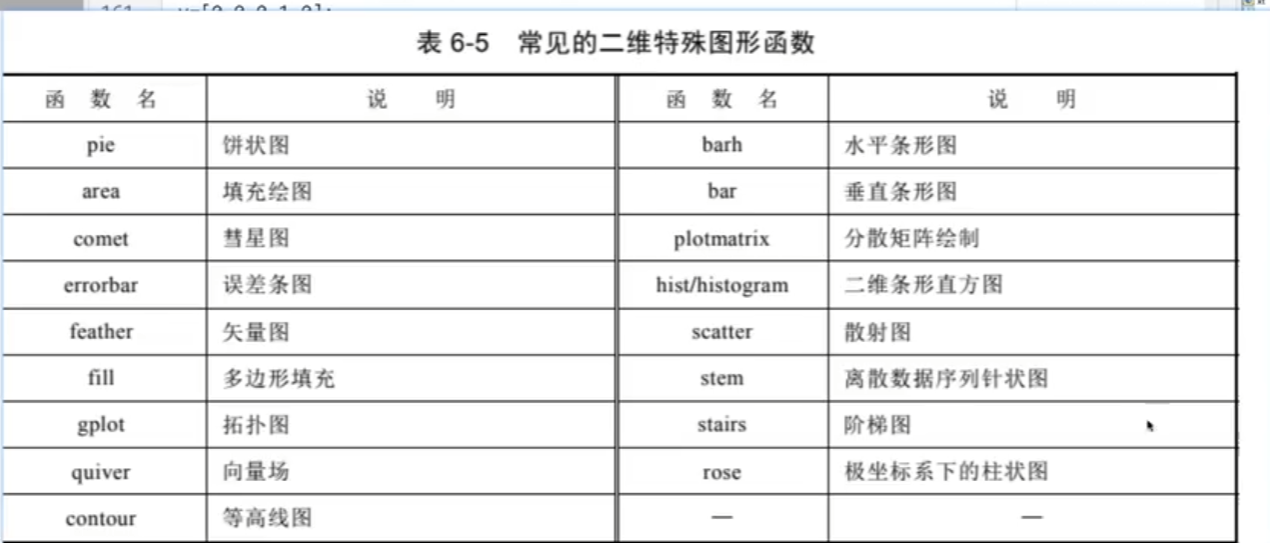
餅狀圖

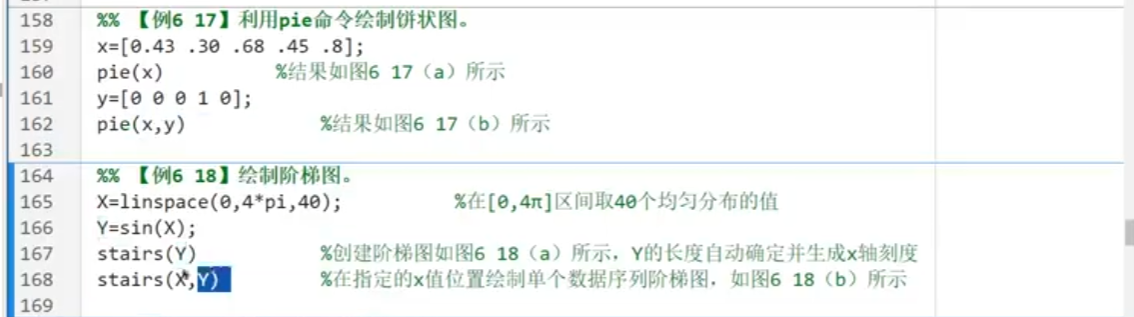
階梯圖

條形圖

等高線

errorbar

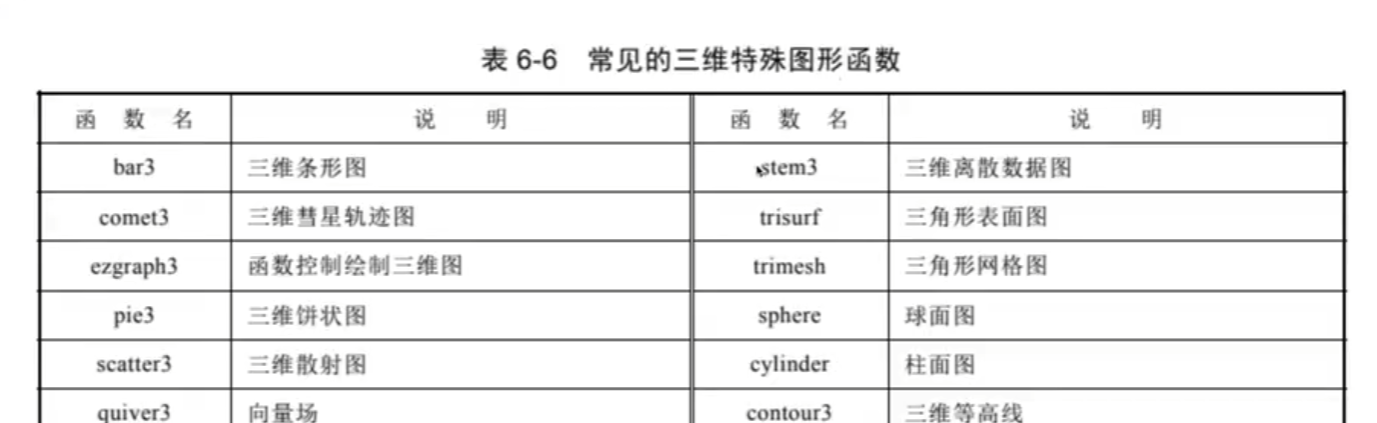
4.三維特殊圖形函數

5.四維

七

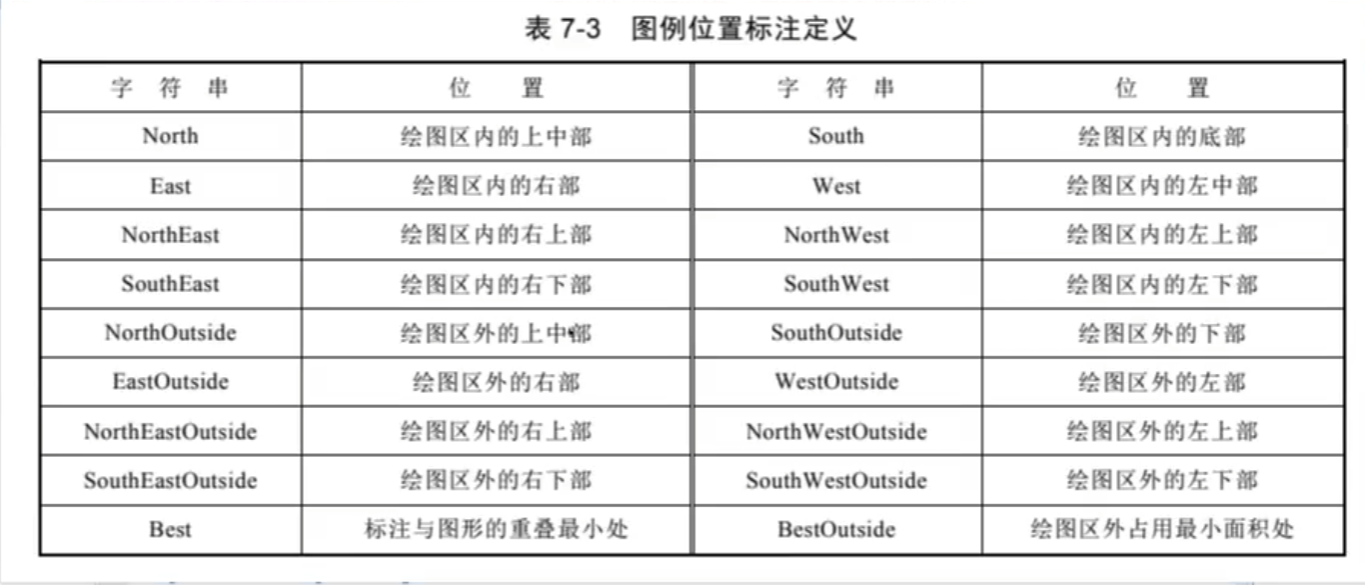
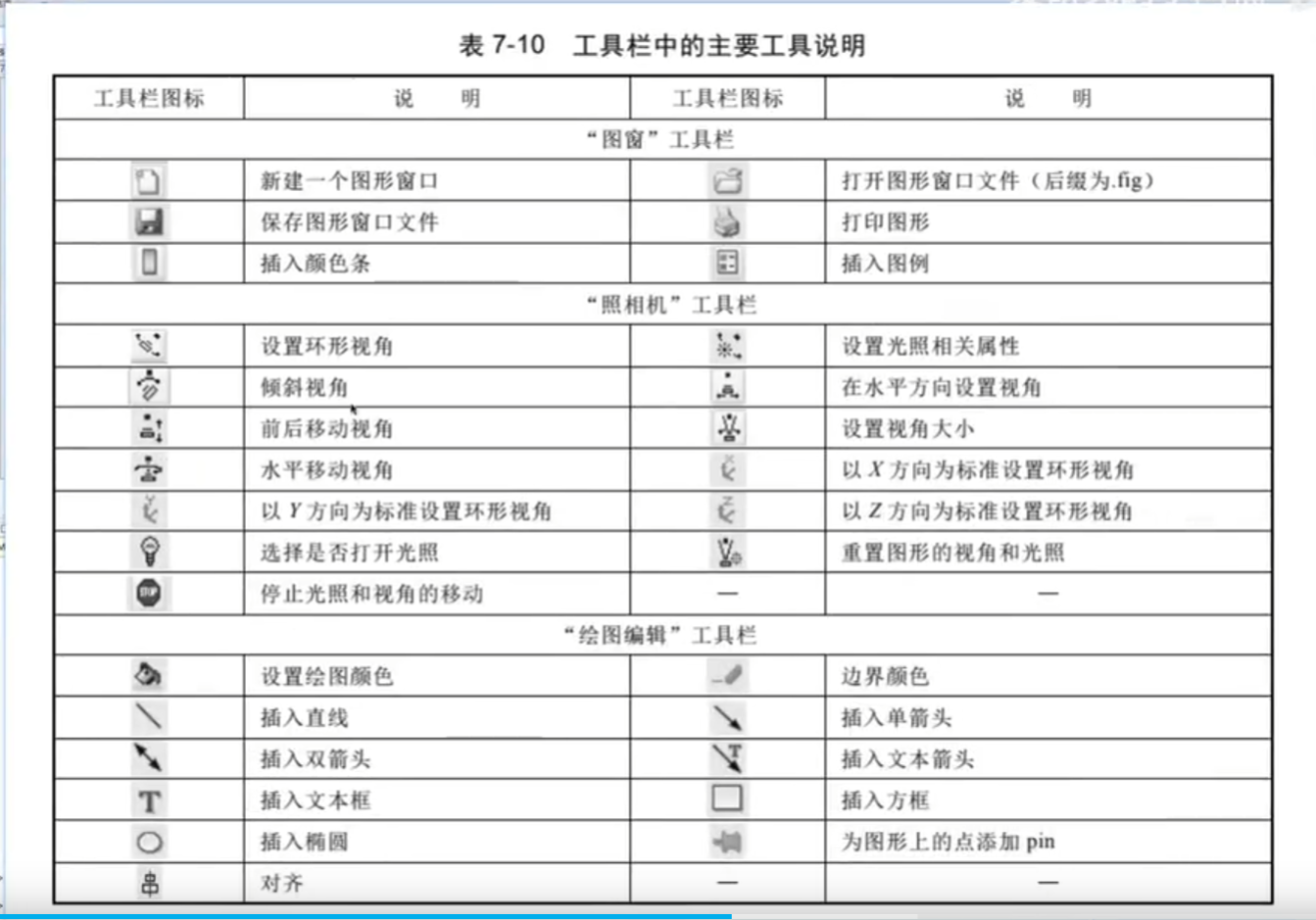
1.坐標軸和圖形標注

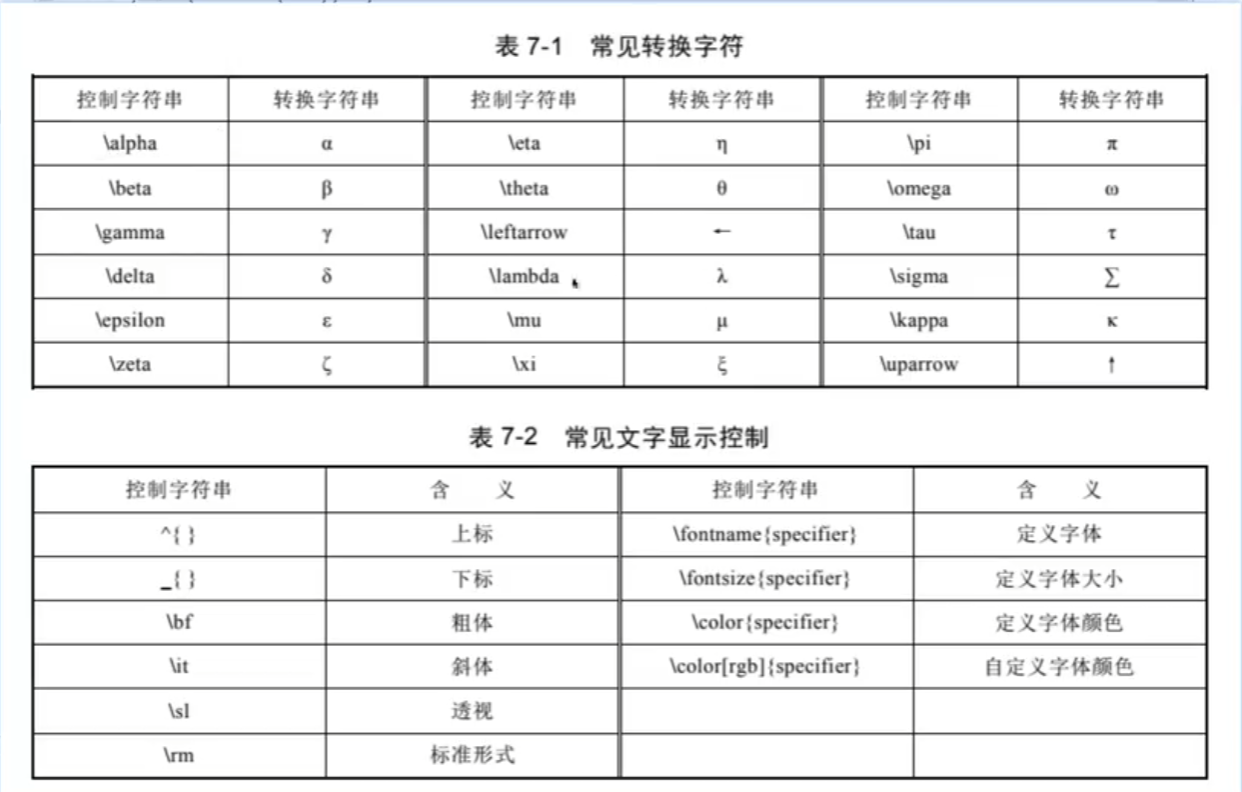
標注：

圖例標注：legend

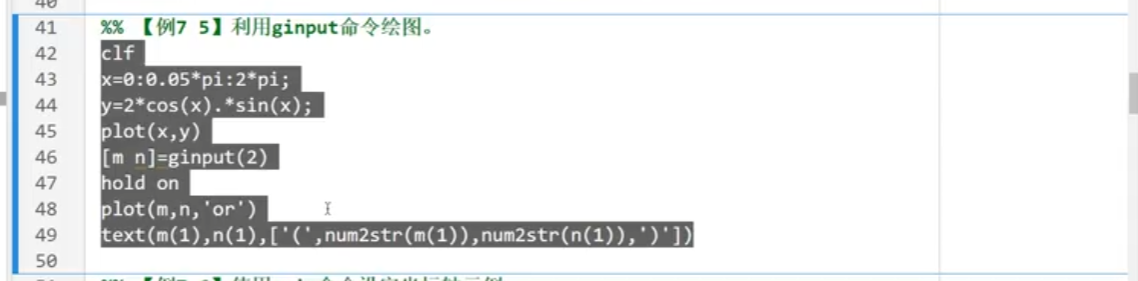
取點：ginput

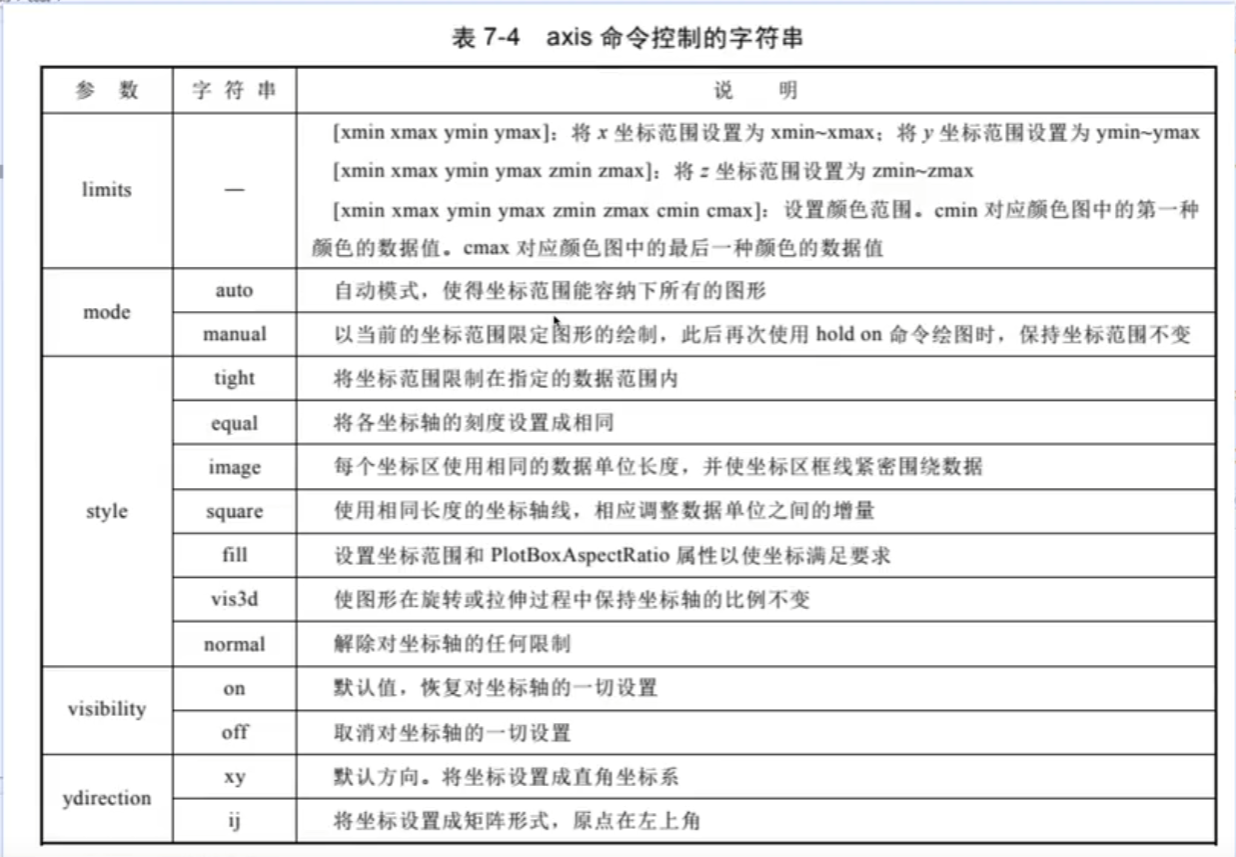
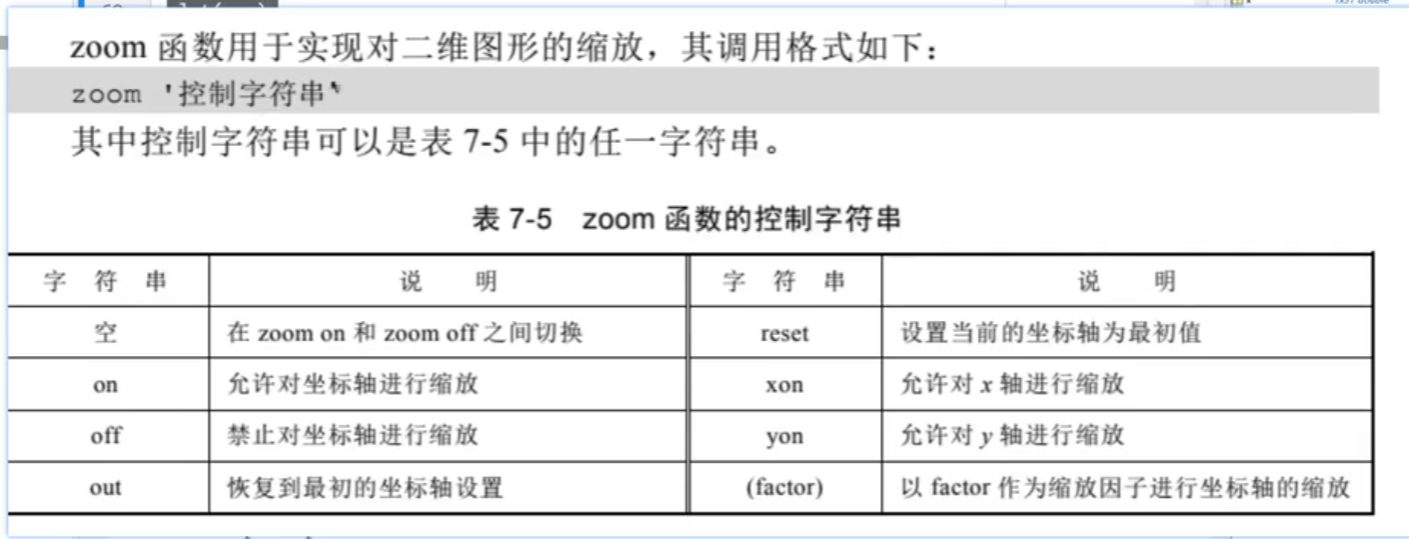
2.命令控制

網格控制

view:觀察點

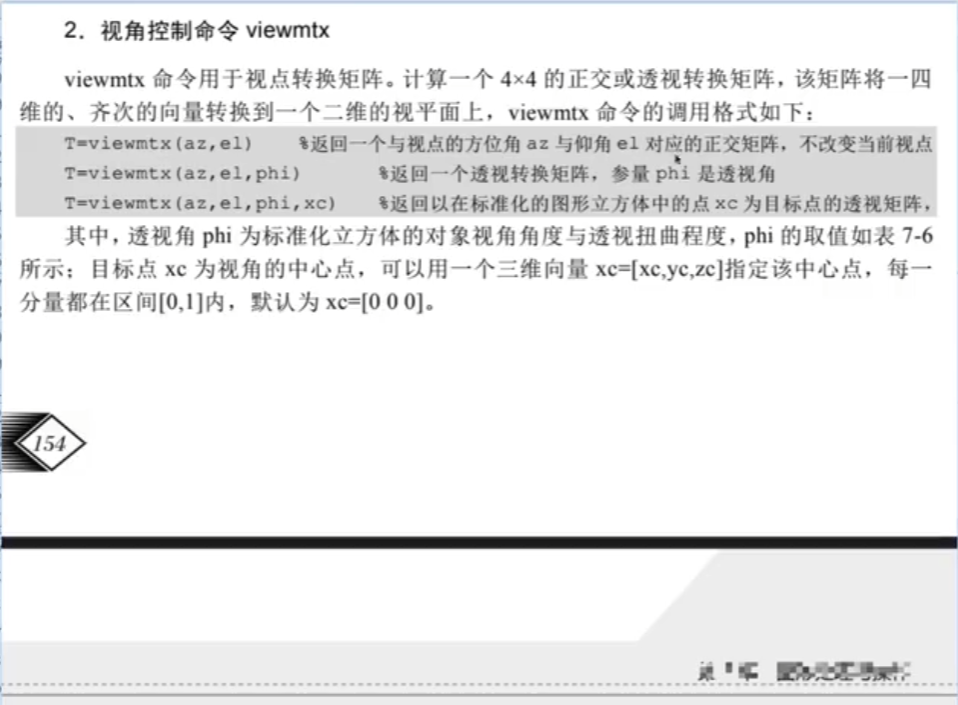
3.顏色

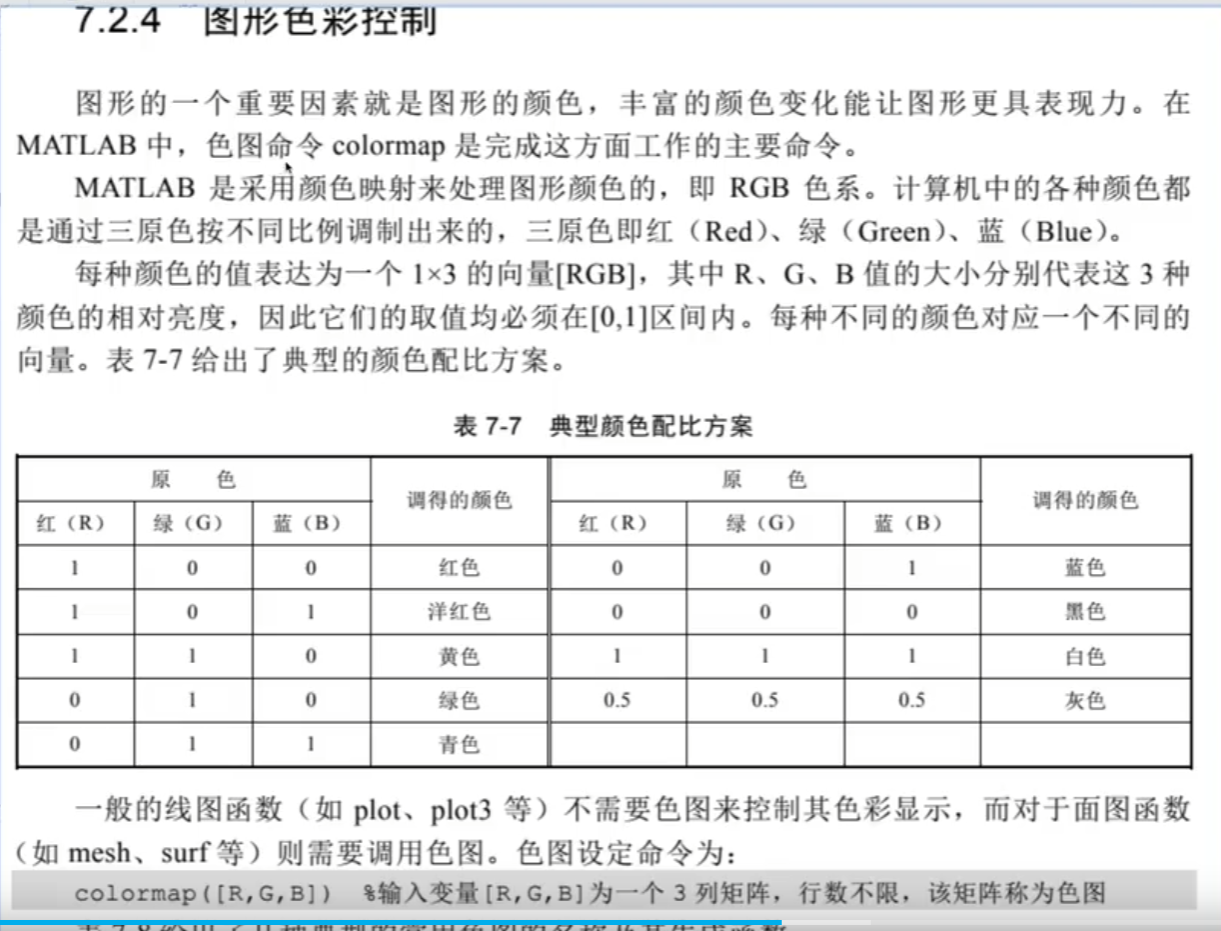
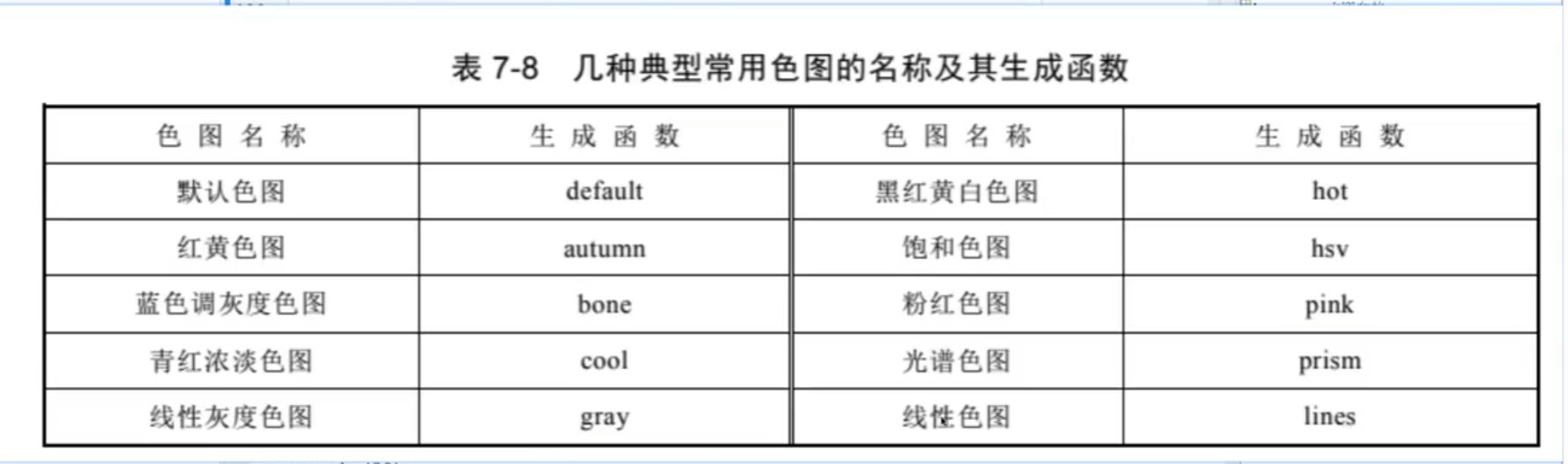
增亮：

顏色標尺：

背景色：

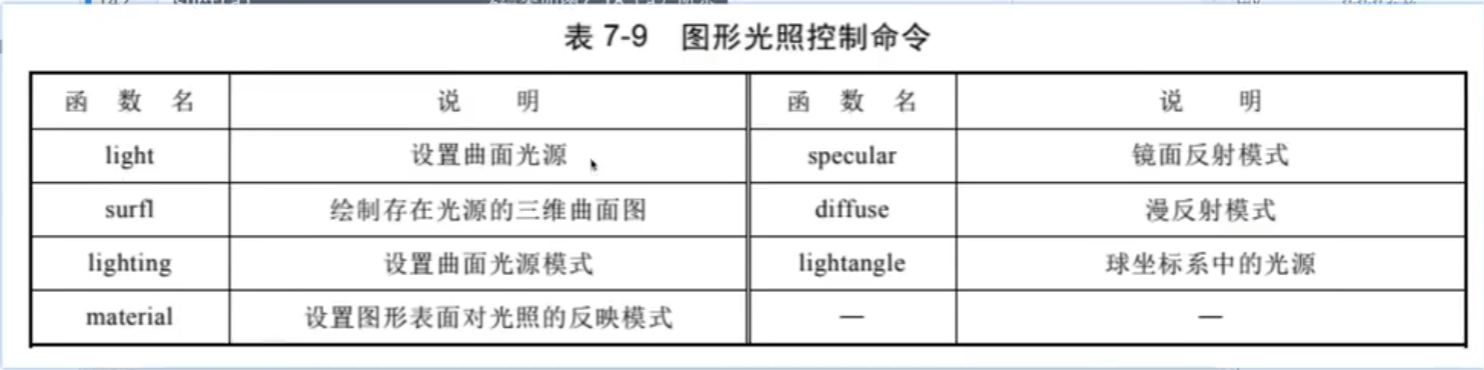
光照設置：

4.圖形窗口

創建：

get獲得圖形窗口屬性；

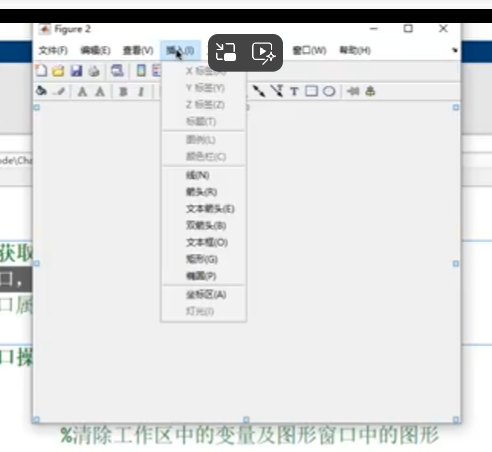
打印或輸出：

八

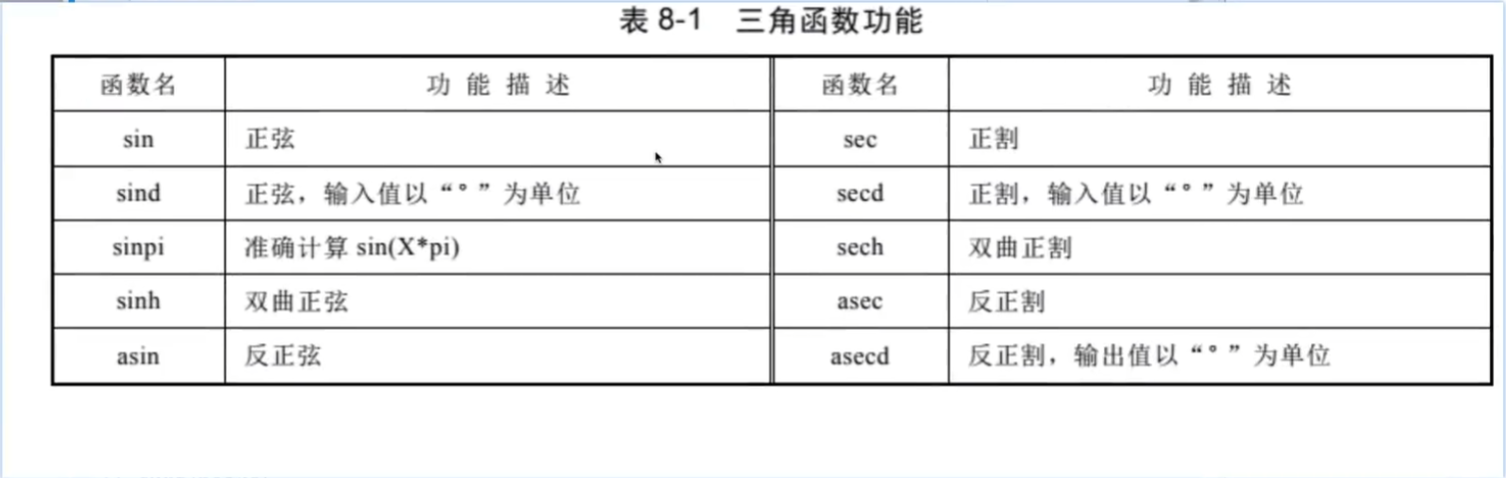
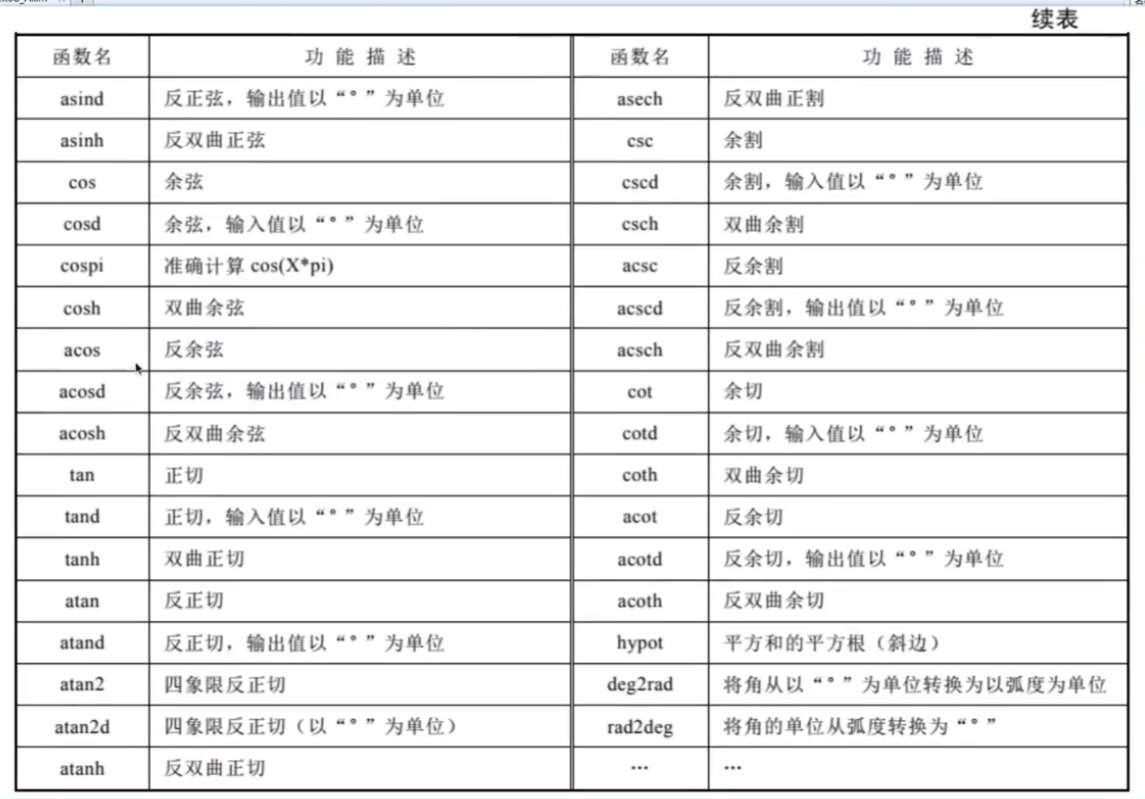
1.數學函數->matlab語言

三角函數：

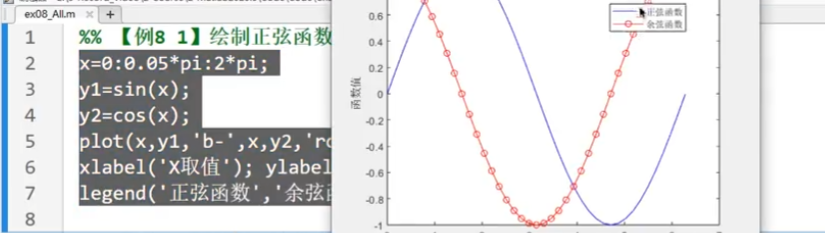
指數對數

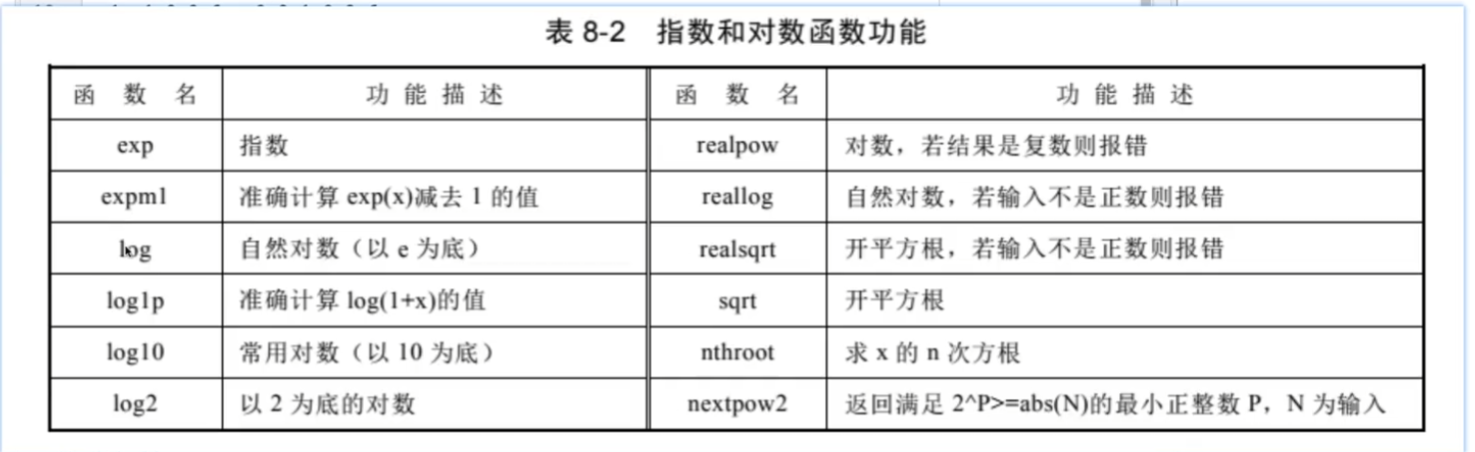復數

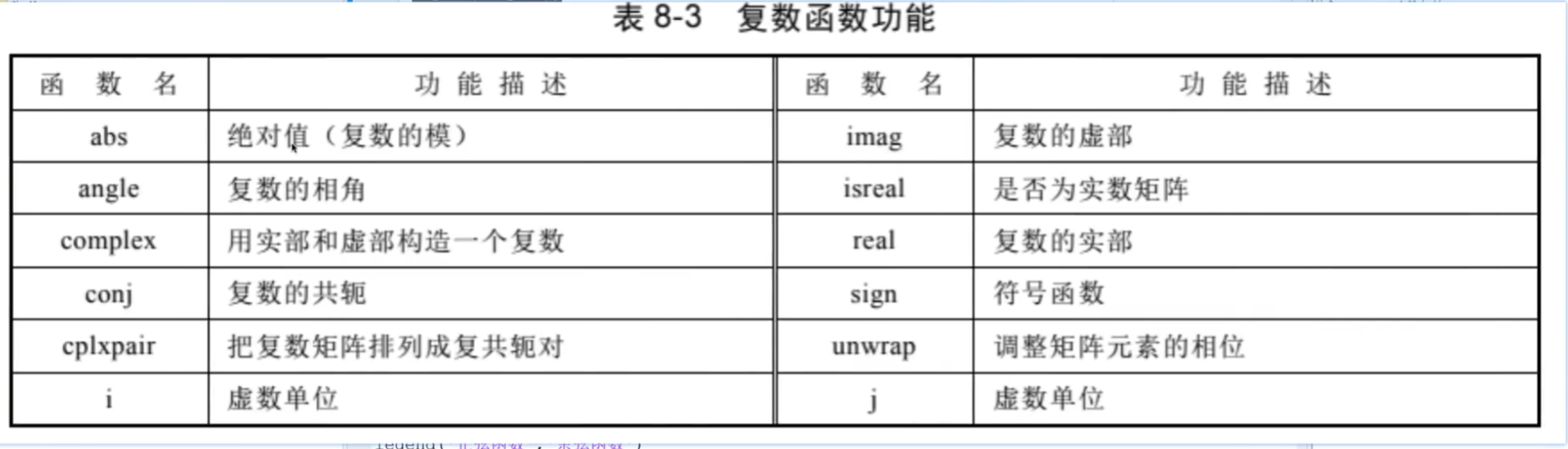
截斷或求余

2.特殊函數

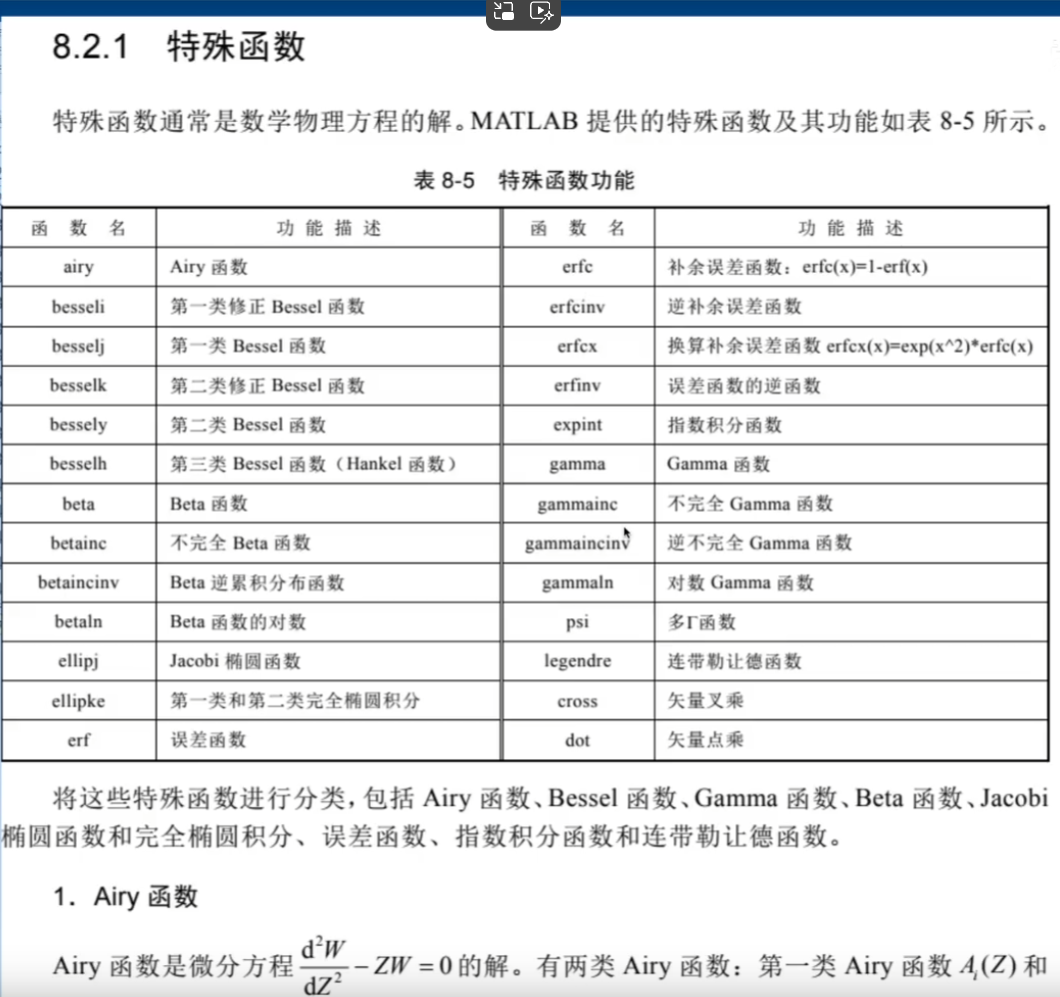
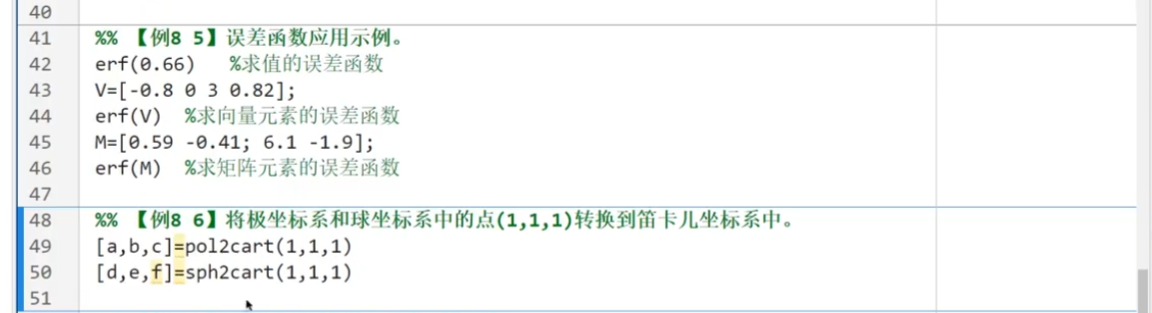
坐標變換函數：

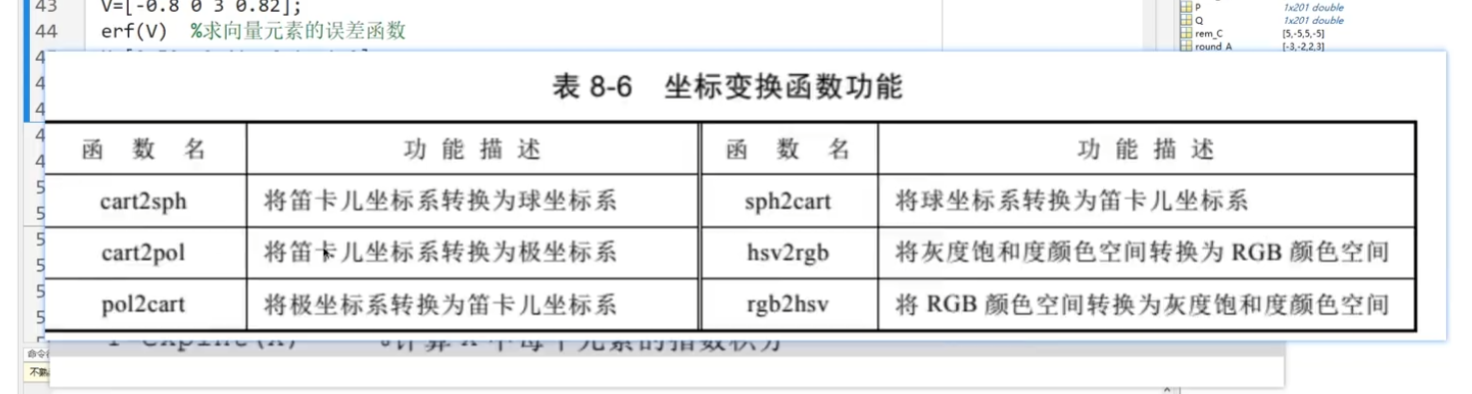數論函數：

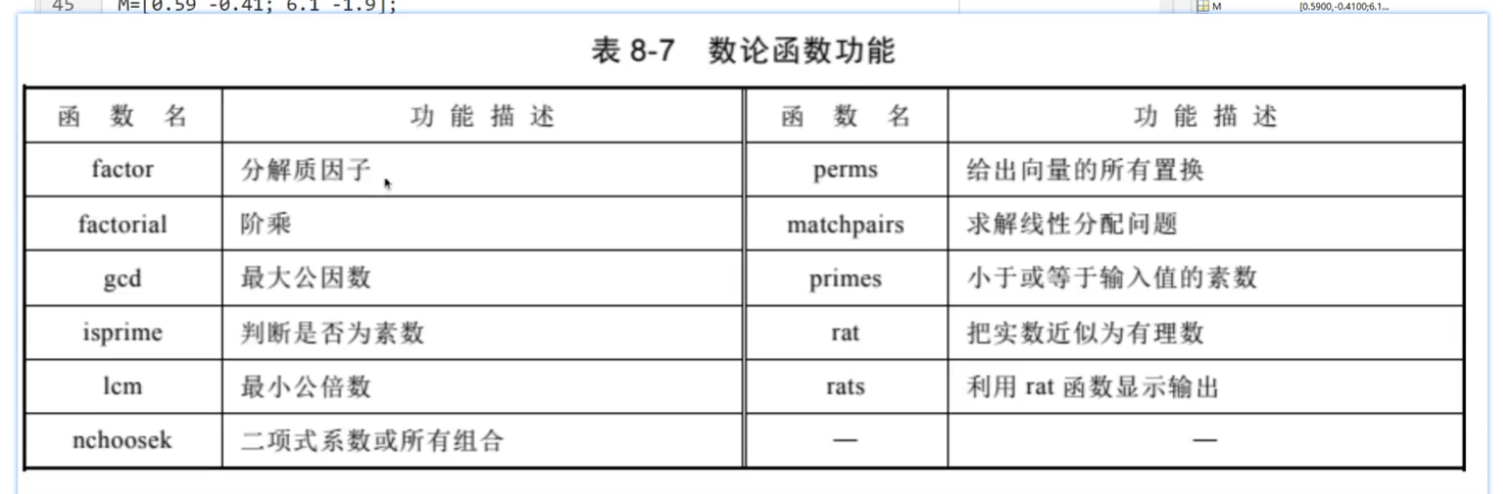
素數

九

1.符號運算

sym:

syms:

class

對象類型

符號運算

化簡：

在 MATLAB 中，符號對象（symbolic object）和普通數值（numeric value）的區別主要體現在數據類型、計算方式、精度、用途等方面。下面我分學術和工程兩個角度給你梳理一下。

1. 數據類型不同

特性	符號對象 (`sym`)	普通數值 (`double`, `single` 等)
數據類型	符號類型（Symbolic）	浮點數類型（Numeric）
存儲形式	存儲的是數學表達式或符號常量，不是近似值	存儲的是有限精度的二進制浮點數
創建方式	`syms x; f = sym('pi');`	`a = 3.1416;`

2. 計算方式不同

符號對象
- 按符號推導規則運算，不會做浮點近似化。
- 能進行代數化簡、微分、積分、解方程等符號運算。
- 例如：
```
syms x
diff(sin(x)^2, x)   % 結果是 2*sin(x)*cos(x)
```
普通數值
- 按數值計算規則運算，采用 IEEE 754 雙精度（或單精度）近似。
- 無法直接進行代數化簡，結果通常是近似數。
- 例如：
```
x = pi/3;
diff(sin(x)^2, x)   % 會報錯，因為 x 只是數值
```

3. 精度與近似

符號對象 → 理論上無限精度（直到內存限制），保留 exact form，如 pi、sqrt(2)。
普通數值 → 有限精度（double 默認約 15~16 位有效數字），存在舍入誤差。

舉例：

sym(pi) - 4*atan(sym(1))   % 結果是 0（完全相等）
pi - 4*atan(1)             % 結果是 0（數值上接近，但可能不是精確 0）

4. 用途上的區別

符號對象
- 符號微積分（diff、int）
- 符號代數（simplify、factor）
- 精確解析解（solve）
- 高精度常數計算（配合 vpa 可指定位數）
普通數值
- 數值仿真（ODE 數值解、FFT 等）
- 工程數值計算（矩陣運算、統計分析等）
- 實時計算與信號處理

5. 轉換關系

數值 → 符號
```
a = 3.14;
sym_a = sym(a);
```

符號 → 數值

x = sym('pi');
double(x)  % 轉為 double 類型近似值

總結表

特性	符號對象 (sym)	普通數值 (double/single)
精度	理論無限精度	有限（~15 位）
運算方式	代數運算	浮點近似運算
用途	推導、符號解、精確計算	數值計算、仿真
內存占用	較大	較小
速度	慢	快

MATLAB 之所以要引入 符號對象（Symbolic Object），本質上是因為數值計算和數學推導的需求是兩類完全不同的任務，而普通浮點數無法滿足后一類任務的精確性與表達能力。

我分幾個層次解釋一下**“為什么需要符號對象”**。

1. 解決浮點數無法表達精確數學對象的問題

普通數值（double、single）存儲的是近似值，而許多數學對象是無法用有限二進制小數精確表示的，比如：

π\pi、ee、2\sqrt{2}
分數 13\frac{1}{3}
無理數、代數式

浮點數在這些情況下會引入舍入誤差，而符號對象則保留精確的數學形式：

sym(pi)   % 保留為 π，不是 3.1416...

2. 支持解析計算（Analytical Computation）

有些任務必須基于公式推導而不是近似數值：

符號微分（得出通用公式，而非某一點的導數）
符號積分（求出積分解析式）
符號解方程（求變量的精確表達式）
代數化簡（消去公共因子、展開或因式分解）

例子：

syms x
diff(sin(x)^2, x)   % 結果是 2*sin(x)*cos(x)，而不是數值

這種能力在通信理論推導、信號公式變換等科研任務中很重要。

3. 實現高精度或任意精度計算

浮點數精度有限（double 約 15~16 位有效數字）。
當需要極高精度（如大數計算、誤差敏感問題）時，浮點運算會累積誤差。
符號對象配合 vpa（Variable Precision Arithmetic）可以按需求設置精度：

vpa(pi, 50)   % 計算 π 的 50 位有效數字

4. 支持數值與推導的混合工作流

在科研和工程計算中，經常需要先推導公式，再數值仿真。

推導階段：用符號對象得到通用解析公式
仿真階段：將符號公式轉成數值函數，高速計算

這種模式可以減少人工推導錯誤，并在參數變化時自動更新公式。
例如 MU-MIMO 信道容量公式推導，可以用符號對象自動完成矩陣求導、跡運算等，再轉為數值形式計算吞吐量。

5. 工程意義

避免手工推導的繁瑣與易錯性（符號引擎自動化）
保證結果的數學嚴謹性（不會因為舍入誤差而得到錯誤結論）
提供可復用的解析模型（直接嵌入到數值計算中）

總結一句

符號對象的存在，是為了讓 MATLAB 不僅能“算數”，還能“做數學”。
它讓 MATLAB 既能做高速的數值計算（仿真），也能做精確的符號推導（理論分析），兩者結合才適用于科研和高精度工程應用。

對，你的理解方向是對的，但我幫你精確化一下：符號變量并不是簡單的“把數值換成變量”，而是把數值、變量甚至表達式都作為數學符號來處理，從而保留它們的精確結構。

1. 普通數值 vs 符號變量的本質區別

普通數值
- 只存儲具體的數（例如 3.1416），MATLAB 只能對它做數值運算。
- 計算結果是數值，沒有“通用性”。
符號變量 / 符號對象
- 存儲的是一個數學符號（例如 xx、π\pi、2\sqrt{2}），可以在運算中保持符號形式，不直接化成數值。
- 能保留變量之間的關系，形成通用公式。
- 計算結果可以是另一個公式，而不是一個單一的數。

2. 例子直觀比較

數值計算

x = pi/3;      % 數值
y = sin(x)^2;  % 已經是數值
diff(y, x)     % ? 報錯，因為 y 是數值，不是表達式

符號計算

syms x
y = sin(x)^2;   % 符號表達式
dy = diff(y, x) % 結果: 2*sin(x)*cos(x)

這里 x 就是一個符號變量，不是具體數值，所以 MATLAB 可以對它做微分、積分、化簡等操作。

3. 不只是變量，還能是“精確數”

符號對象還可以表示常數的精確形式：

sym(1/3)     % 保留為 1/3
1/3          % double 結果是 0.3333...

這意味著符號對象不僅僅是 “未知量 xx”，也可以是一個精確常數或一個代數式。

4. 總結你的那句話

符號變量并非簡單地將數值替換為變量，而是以符號形式存儲數學對象（變量、常數或表達式），使其在運算中保留解析結構，從而能夠生成通用公式，而不僅是針對特定數值的結果。

MATLAB符號變量的創建和簡單運算-CSDN博客

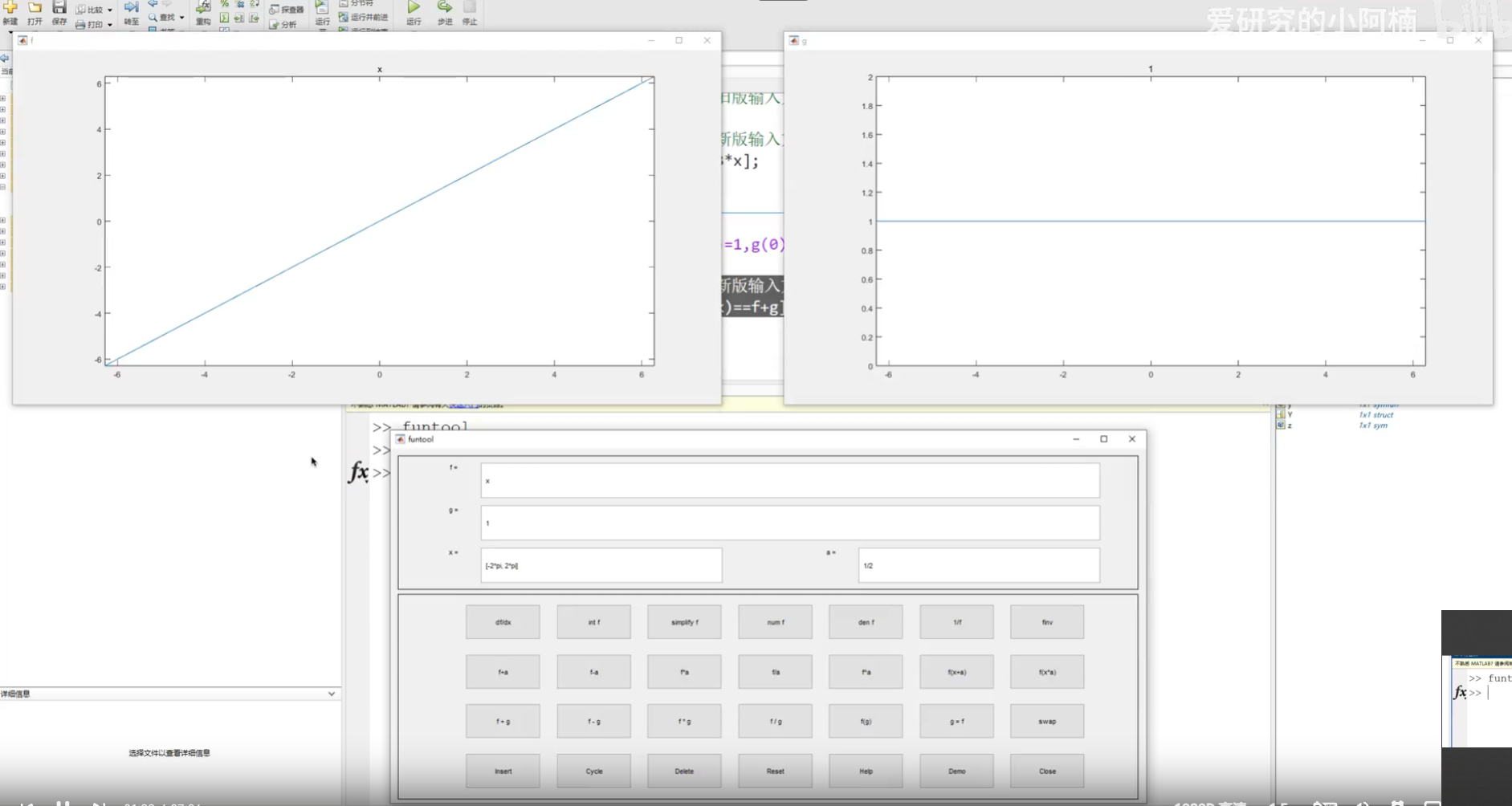
2.符號表達式

作為一個公式；

極限：

求和：

泰勒：

積分：

傅里葉變換：

eg:階躍函數

拉普拉斯變換：

eg:

Z變換：

eg:

3.符號矩陣運算

4.符號方程求解

5.可視化數學分析窗口

泰勒級數分析：

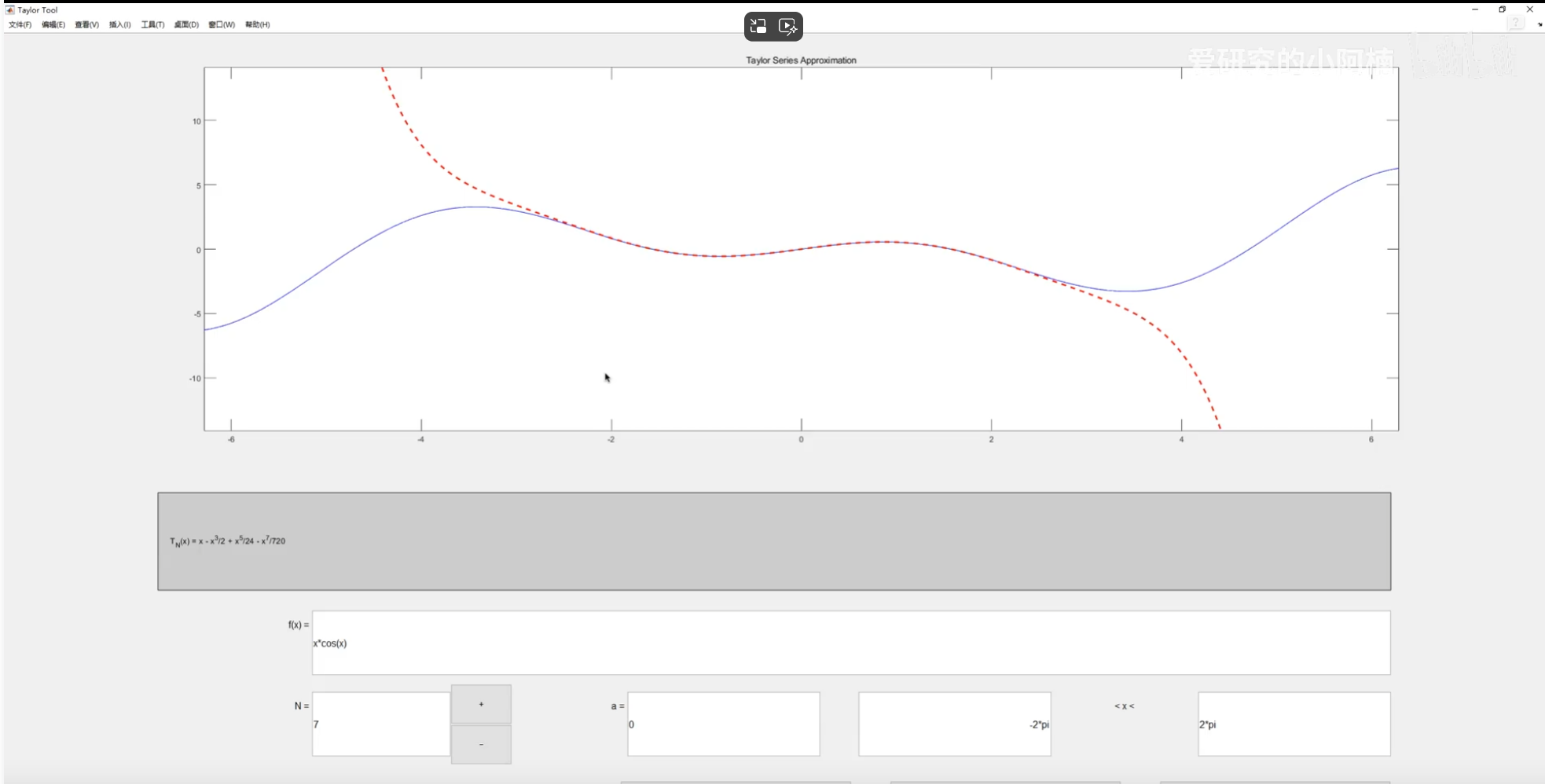
總結

是的，你現在已經抓到符號對象的核心特性了。
更精確地說，符號對象可以在兩種“模式”下使用：

1. 作為“表達式”運算（符號模式）

所有變量、矩陣、公式保持符號形式，不轉成具體數值。
運算結果依舊是另一個公式（而不是數）。
常見用途：推導公式、化簡表達式、符號微分/積分、符號解方程等。

例子：

syms x y
f = sin(x)^2 + y^2;   % 符號表達式
dfdx = diff(f, x)     % 結果是 2*sin(x)*cos(x)

2. 對符號賦值求數值（數值模式）

可以用 subs 將符號變量替換成具體值，再用 double 轉換為數值。
常見用途：公式推導完成后，用特定參數計算結果。

例子：

syms x y
f = sin(x)^2 + y^2;f_sub = subs(f, [x y], [pi/3 2]);  % 用具體值替換符號
num_result = double(f_sub)         % 轉成 double 類型數值

3. 符號矩陣同理

推導階段：符號矩陣保留精確結構，可做代數運算（行列式、逆、跡等）。
計算階段：賦值并數值化求具體結果。

例子：

syms a b c d
A = [a b; c d];
det_A = det(A)          % 結果是 a*d - b*c （公式）
det_num = double(subs(det_A, [a b c d], [1 2 3 4])) % 結果是 -2

? 總結
你完全可以先用符號對象推導出通用表達式（保持解析精度），然后在需要時給符號變量賦值求數值。
這種“先符號推導 → 再數值計算”的模式特別適合通信系統公式推導 + 仿真這類科研任務，因為能避免手算公式的易錯性，又能在仿真中復用公式。

十

數值計算：

求解方案：

高斯：

迭代法：對高階

插值：

插值（Interpolation）在數學和信號處理里，指的是已知一組離散數據點，通過一定方法推算這些點之間未知位置的值。
它的本質就是——用一個連續函數去“穿過”這些已知點，然后用它估計中間點。

1. 插值的基本概念

假設你知道某函數在 x0,x1,…,xnx_0, x_1, \dots, x_n 處的值 y0,y1,…,yny_0, y_1, \dots, y_n，
插值的目標就是構造一個函數 P(x)P(x)，使得：

P(xi)=yi,i=0,1,…,nP(x_i) = y_i, \quad i=0,1,\dots,n

并用 P(x)P(x) 來估算這些已知點之間的任意位置的值。

2. 插值 vs 擬合

插值：要求插值函數嚴格通過所有已知數據點，沒有偏差。
擬合：允許擬合曲線與數據點有一定誤差，更關注整體趨勢（比如最小二乘法擬合）。

3. 常見插值方法

方法	特點	舉例
線性插值 (Linear)	相鄰兩點之間用直線連接，簡單快速	`interp1(x, y, xq, 'linear')`
多項式插值 (Polynomial)	用高次多項式穿過所有點	拉格朗日插值、多項式插值公式
分段三次樣條插值 (Cubic Spline)	分段三次多項式，保證一階、二階導數連續，曲線平滑	`interp1(x, y, xq, 'spline')`
二維/多維插值	適用于二維/三維數據	`interp2`、`interpn`
傅里葉插值	用周期信號的頻域展開做插值	信號處理中的帶限插值

4. MATLAB 中的插值示例

x = [0 1 2 3];
y = [0 1 0 1];xq = 0:0.1:3;  % 查詢點
y_linear = interp1(x, y, xq, 'linear'); % 線性插值
y_spline = interp1(x, y, xq, 'spline'); % 樣條插值plot(x, y, 'o', xq, y_linear, '-', xq, y_spline, '--');
legend('原始點', '線性插值', '樣條插值');

5. 工程與科研中的意義

信號處理：將離散采樣信號恢復到連續時間（帶限插值）。
通信系統：定時同步、信道估計中利用插值獲得未采樣點的信道響應。
數值計算：在已知離散解的情況下估算中間值（如有限元分析）。
圖像處理：圖像縮放（最近鄰插值、雙線性插值、雙三次插值）。

📌 一句話總結：

插值是“已知幾個點，填補中間的空白”的過程，本質上是用一個連續函數通過這些點，然后用它預測未知點的值。

擬合：

polyfit 和 polyval 是 MATLAB 里一對常用的多項式擬合 + 計算工具，它們經常配合使用，但作用不同：

1. `polyfit` —— 求多項式系數（擬合階段）

作用：給定一組數據點，找到一個指定階數的多項式，使它在最小二乘意義下盡量接近這些數據。

語法：

p = polyfit(x, y, n)

x、y：數據點（長度相同的向量）
n：擬合多項式的階數
p：返回一個行向量，包含從高次項到常數項的系數

例子：

x = [1 2 3 4];
y = [2.2 2.8 3.6 4.5];
p = polyfit(x, y, 1)   % 一階擬合（直線）
% p 可能返回 [0.77 1.45]，對應 0.77*x + 1.45

2. `polyval` —— 計算多項式值（預測階段）

作用：根據多項式系數，計算多項式在某些點的值。

語法：

y_fit = polyval(p, xq)

p：由 polyfit 返回的系數向量
xq：要計算的自變量值（可為標量、向量或矩陣）
y_fit：對應的多項式值

例子：

xq = 1:0.5:4;       % 查詢點
yq = polyval(p, xq) % 根據擬合多項式預測

3. `polyfit` + `polyval` 組合使用示例

% 原始數據
x = [1 2 3 4];
y = [2.2 2.8 3.6 4.5];% 用二階多項式擬合
p = polyfit(x, y, 2);% 生成更密的 x 值進行預測
xq = linspace(1, 4, 100);
yq = polyval(p, xq);% 繪圖
plot(x, y, 'o', xq, yq, '-');
legend('原始數據', '二階擬合曲線');

4. 和插值的區別

插值：要求曲線經過所有原始點（誤差為 0）。
polyfit 擬合：允許曲線不經過所有點，目標是最小化總體誤差（最小二乘法）。
多項式插值也能用 polyfit 實現，但擬合階數要等于數據點數減 1（容易震蕩）。

? 總結

polyfit：求多項式系數（擬合/插值）
polyval：用系數計算多項式值（預測/繪制）
常用組合：
先 polyfit 找系數 → 再 polyval 畫曲線或求值

如果你需要，我可以幫你畫一張**“polyfit vs 插值”對比圖**，讓你直觀看到同一組點用線性擬合、二次擬合、樣條插值的區別。這樣你在科研（比如 MU-MIMO 信道曲線建模）時能快速判斷用哪種方法。

問題

問題1：asv是什么類型文件

有時在存放m文件的文件夾中會出現*.asv
　　asv 就是auto save的意思，*.asv文件的內容和相應的*.m文件內容一樣，用記事本和matlab都能打開它。它可以作為*.m文件的“備份”。
　　可以在preference中通過設置取消自動備份功能：file->preferences->editor/debugger-->auto save,uncheck "autosave on" checkbox ，把勾選去掉就行了。