太陽平近點角詳解:概念、計算與應用
1. 基本定義
**太陽平近點角(Mean Anomaly,M)**是描述天體(如地球)在其軌道上平均運動位置的角度參數。對于太陽系中的行星或衛星而言,它表示假設天體以恒定角速度運動時,從近日點開始計算的理論角度位置。
2. 軌道力學基礎
在二體問題中,天體運動遵循開普勒定律:
- 開普勒第一定律:行星軌道是橢圓,太陽位于橢圓的一個焦點
- 開普勒第二定律:行星與太陽連線在相等時間內掃過相等面積
- 開普勒第三定律:軌道周期的平方與半長軸的立方成正比
3. 平近點角計算公式
3.1 基本公式
M = M? + n(t - t?)
其中:
- M?:歷元時刻t?的平近點角
- n:平均角速度(n = 2π/T,T為軌道周期)
- t:當前時刻
3.2 地球繞太陽運動的平近點角(J2000歷元)
對于地球:
M = 357.52911° + 0.98560028°·d
其中d是從J2000.0起算的儒略日數
4. 相關概念對比
| 參數 | 定義 | 計算公式 | 物理意義 |
|---|---|---|---|
| 平近點角(M) | 假設勻速運動時的角度 | M = M? + n(t-t?) | 理論平均位置 |
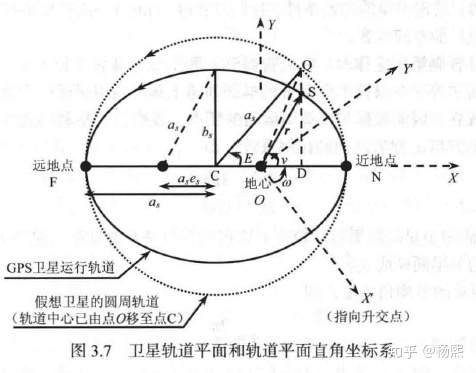
| 真近點角(ν) | 實際位置與近日點的角度 | 需解開普勒方程 | 實際觀測位置 |
| 偏近點角(E) | 輔助計算用的角度 | M = E - e·sinE | 計算真近點角的中間量 |
5. 計算步驟示例
計算2023年1月1日地球的平近點角:
-
計算從J2000.0(2000年1月1日12:00 TT)到2023年1月1日0:00 UTC的日數:
- 約8400.5天
-
代入公式:
M = 357.52911° + 0.98560028°×8400.5≈ 357.52911° + 8280.5°≈ 8638.0° ≈ 358.0° (減去360°的整數倍)
6. 實際應用
6.1 軌道位置計算
通過平近點角→偏近點角→真近點角的轉換,確定天體精確位置
6.2 太陽歷法
用于計算太陽赤緯、日出日落時間等
6.3 航天任務
衛星軌道預報和軌道機動計算的基礎參數
7. 現代計算工具
- NASA/NAIF SPICE工具包:提供精確的星歷計算
- SOFA天文庫:IAU標準算法實現
- VSOP87行星理論:高精度行星位置計算
8. 注意事項
- 歷元選擇:不同歷元(如J2000、B1950)的M?不同
- 時間系統:需統一使用TT或TDB時間
- 軌道攝動:長期計算需考慮其他天體的引力攝動
太陽平近點角作為軌道力學的基礎參數,是連接理論計算與實際觀測的重要橋梁,在航天工程和天文研究中具有不可替代的作用。



















