01數據結構-圖的鄰接矩陣和遍歷

1.圖的遍歷
- 1.1深度優先遍歷
- 1.2廣度優先搜索
2.鄰接矩陣的代碼實現

1.圖的遍歷

1.1深度優先遍歷

深度優先搜索的過程類似于樹的先序遍歷，首先從例子中體會深度優先搜索，例如下圖1是個無向圖，采用深度優先算法遍歷這個圖的過程是：

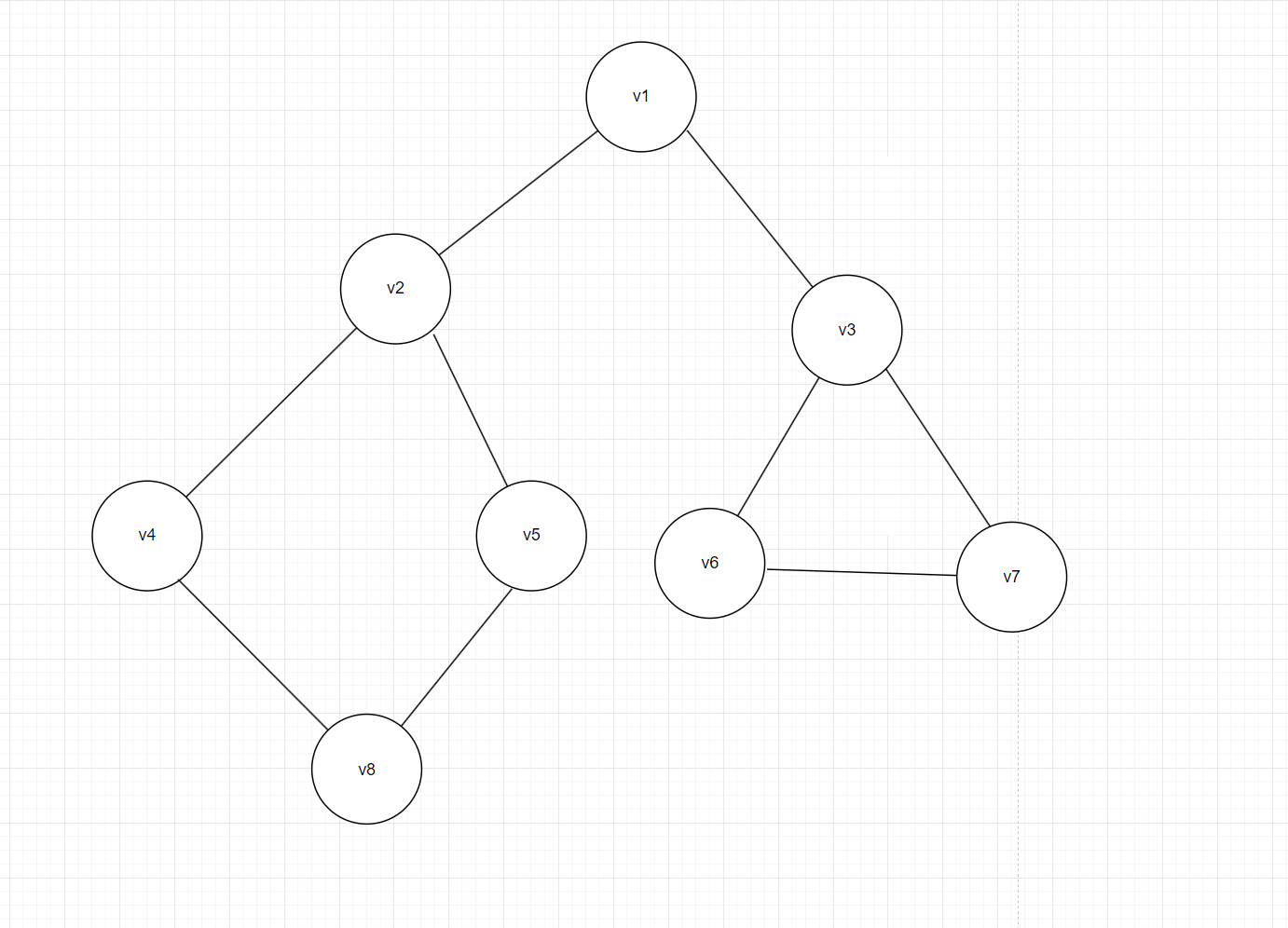
圖1

1.首先任意位置找一個未遍歷過的頂點，例如從v1開始，由于v1率先訪問過了，所以，需要標記v1的狀態為訪問過；
2.然后遍歷v1的鄰接點，例如訪問v2,并做標記，然后訪問v2的鄰接點，例如v4（做標記）,然后v8，然后v5；
3.當繼續遍歷v5的鄰接點時，根據之前的標記顯示，所有鄰接點都被訪問過了。此時，從v5回到v8，看v8是否有未被訪問過的鄰接點，如果沒有，繼續回到v4,v2,v1;
4.通過查看v1,找到一個未被訪問過的頂點v3,繼續遍歷,然后訪問v3，鄰接點v6,然后v7。
5.由于v7沒有未被訪問過的鄰接點，所以退回到v6,繼續退回到v3,最后到達v1,發現沒有未被訪問的；
6.結束遍歷。

這里需要引入已訪問的數組Visited，用來標識哪些點被訪問了。因為圖中的元素比時n:m，遍歷的時候如果不引入會出現同一個頂點遍歷多次的情況。

1.2廣度優先搜索

廣度優先搜索的過程類似于樹的廣度優先搜索，首先從例子中體會廣搜，例如圖1是個無向圖，采用廣搜算法遍歷這個圖的過程是：

1.首先任意位置找一個未遍歷過的頂點，例如v1,在看到這個v1后，把這個頂點的所有鄰接點v2,v3，放進隊列中,標記v1的狀態為訪問過；
2.v1訪問后訪問v2,把v2的所有鄰接點且沒有被訪問過的點(v4,v5)入隊，標記v2的狀態為訪問過；
3.v2訪問后訪問v3,把v3的所有鄰接點且沒有被訪問過的點(v6,v7)入隊，標記v3的狀態為訪問過；
4.重復上述過程，直到所有頂點遍歷完;
5.結束遍歷。

值得注意的是這個Visited數組，我們在入隊的時候就可以設置為已經訪問過的元素，我們的處理是訪問出隊的頂點，并把出隊的頂點的鄰接點入隊。

2.鄰接矩陣的代碼實現

鄰接矩陣的頂點結構：

//鄰接矩陣的頂點結構，表示一個頂點的信息
typedef struct{int no;     //頂點編號char *show; //顯示行為(我們不希望打印數字no出來，而是空間中存的數據)
}MatrixVertex;

圖的鄰接矩陣表示法：

typedef int MatrixEdge;
//圖的鄰接矩陣表示法
typedef struct {MatrixVertex vex[MaxNodeNum];               // 存儲頂點信息，使用一維數組存儲頂點MatrixEdge edges[MaxNodeNum][MaxNodeNum];   // 存儲邊的結構，矩陣,數組中存的是權值int nodeNum;                                // 約束實際的頂點數量//<----------上面三個其實就夠了，為了表示任意圖，加了下面兩個變量------------->int edgeNum;                                //邊的數量int directed;                               //是否有向
}MatrixGraph;

因為鄰接矩陣的邊就是個二維矩陣，所以不把它封裝成結構體了，直接構建鄰接矩陣，參照的是《01數據結構-圖的概念和圖的存儲結構》鏈接: https://blog.csdn.net/2302_82136376/article/details/150055797?fromshare=blogdetail&sharetype=blogdetail&sharerId=150055797&sharerefer=PC&sharesource=2302_82136376&sharefrom=from_link中的邏輯。

初始化鄰接矩陣的接口：

void initMatrixGraph(MatrixGraph *graph,const char *names[],int num,int directed,int edgeValue);void addMGraphEdge(MatrixGraph *graph,int x,int y,int w);

先看void initMatrixGraph(MatrixGraph *graph,const char *names[],int num,int directed,int edgeValue);中的參數，第一個傳的是哪一個圖，第二個傳的是一個字符串數組用于初始化MatrixVertex中的char *show，第三個傳的是約束實際的頂點數量，第四個傳的是是否有向，第五個傳的是每條邊的權重，

再看void addMGraphEdge(MatrixGraph *graph,int x,int y,int w);給圖中的兩個頂點添加邊，所以需要MatrixGraph *graph,int x,int y，再給這條邊加權重所以傳int w。

初始化實現：void initMatrixGraph(MatrixGraph *graph,const char *names[],int num,int directed,int edgeValue);

void initMatrixGraph(MatrixGraph *graph, const char *names[], int num, int directed, int edgeValue) {graph->directed=directed;graph->nodeNum=num;graph->edgeNum=0;memset(graph->vex,0,sizeof(graph->vex));memset(graph->edges,0,sizeof(MatrixEdge) * MaxNodeNum * MaxNodeNum);for (int i = 0; i < num; ++i) {graph->vex[i].no=i;graph->vex[i].show=names[i];for (int j = 0; j < num; ++j) {//存權值graph->edges[i][j]=edgeValue;}}
}

先初始化圖中的頂點數量為傳入的頂點數量，將傳入函數的圖中的頂點集和邊集權初始化為0。for循環開始為MatrixVertex中的頂點編號和顯示行為賦值，進入第二重循環，為邊集里的每一條賦權重

添加邊：void addMGraphEdge(MatrixGraph *graph,int x,int y,int w);

static int isEdge(int weight) {if (weight > 0 && weight < INF) {return 1;}return 0;
}void addMGraphEdge(MatrixGraph *graph, int x, int y, int w) {if (x<0 || x>graph->nodeNum) {return;}if (y<0 || y>graph->nodeNum) {return;}if (!isEdge(graph->edges[x][y])) {graph->edges[x][y]=w;//對角線另外一條邊也添加if (graph->directed == 0) {graph->edges[y][x] = w;}graph->edgeNum++;}
}

在static中我們寫了一個判斷圖中兩個頂點之間是否有邊的內在接口函數，采用的方式是權值判斷法，如果傳入的邊的權值大于0并且小于一個極大值，我們就認為這兩個頂點之間有邊，反之則無邊。在void addMGraphEdge(MatrixGraph *graph, int x, int y, int w)函數中假設沒有邊，即isEdge(graph->edges[x][y])返回值為0，我們就連接兩條邊，并賦權重，如果graph->directed == 0我們就認為是個無向圖，由于邊的矩陣是對稱矩陣，我們把對角線另外一條邊也添加。

來小小測試一下;

#include <stdio.h>
#include <stdlib.h>
#include "matrixGraph.h"void testMatrixGraph(MatrixGraph *grap) {char *nodeName[] = {"V1", "V2", "V3", "V4", "V5", "V6", "V7", "V8"};initMatrixGraph(grap, nodeName, sizeof(nodeName) / sizeof(nodeName[0]), 0, 0);addMGraphEdge(grap, 0, 1, 1);addMGraphEdge(grap, 0, 2, 1);addMGraphEdge(grap, 1, 3, 1);addMGraphEdge(grap, 1, 4, 1);addMGraphEdge(grap, 2, 5, 1);addMGraphEdge(grap, 2, 6, 1);addMGraphEdge(grap, 3, 7, 1);addMGraphEdge(grap, 4, 7, 1);addMGraphEdge(grap, 5, 6, 1);
}int main() {MatrixGraph g1;testMatrixGraph(&g1);printf("graph have %d edge!\n", g1.edgeNum);return 0;
}

結果:

D:\work\DataStruct\cmake-build-debug\03_GraphStruct\MatrixGraph.exe
graph have 9 edge!進程已結束，退出代碼為 0

下面來看深度優先遍歷和廣度優先遍歷的代碼

深度優先遍歷：void DFS_MGraph(MatrixGraph *graph,int v);

static int MGraphVisited[MaxNodeNum];void visitMGraphNode(MatrixVertex* node) {printf("%s\t", node->show);
}void DFS_MGraph(MatrixGraph *graph,int v) {visitMGraphNode(&graph->vex[v]);MGraphVisited[v]=1;for (int i = 0; i < graph->nodeNum; ++i) {if (isEdge(graph->edges[v][i])&&MGraphVisited[i]==0) {DFS_MGraph(graph,i);}}
}

寫了一個數組來存已經訪問過的頂點，由于類似于樹的先序遍歷，所以函數進來就要訪問，然后把傳入的頂點設為已被訪問，進入for循環從0號頂點一直遍歷到graph->nodeNum，判斷有哪個頂點與他右邊并且未被訪問，如果找到進入遞歸，一直遞到第一次傳入的頂點v找遍graph->nodeNum這么多頂點，退出遞歸函數。

如圖2我們假設傳入的時0即a這個頂點，訪問a，把a標記為已被訪問(紅色)，進入函數的for循環，發現了和1即b頂點間有邊且b還未被訪問，執行DFS_MGraph(graph,i);

第一次遞進去，傳入的是1即b頂點，把b標記為已被訪問(藍色)，發現和0即a頂點間有邊但是a已被訪問，繼續遍歷發現和2即c頂點有邊且c頂點未被訪問，執行DFS_MGraph(graph,i);

第二次遞進去，傳入的是2即c頂點，把c標記為已被訪問(綠色)，發現和1即b頂點間有邊但是b已被訪問，繼續遍歷發現和3即d頂點有邊且d頂點未被訪問，執行DFS_MGraph(graph,i);

第三次遞進去，傳入的是3即d頂點，把d標記為已被訪問(黃色)，發現和0即a頂點間有邊但是b已被訪問，繼續遍歷發現和2即c頂點有邊但是c頂點也已訪問，一直for循環到把5個頂點全部循環完也沒有找到開始歸回去

第一次歸，由于是從第二次遞歸的黃顏色進來的，所以歸回到第二次遞歸的黃顏色格子，在第4個頂點即e有邊且e頂點未被訪問，執行DFS_MGraph(graph,i);

第四次遞進去，此時全部頂點都被訪問，所以開始歸回。

第二次歸，直接歸回到第四行的紫色格子

第三次歸，函數執行完再次歸回到第三行的綠色格子，由于全部頂點都被訪問所以再歸回去。

第四次歸，歸到第二行的藍色格子，全部頂點都被訪問，直接for循環完后退出函數。最終深搜的順序：a->b->c->d->e。

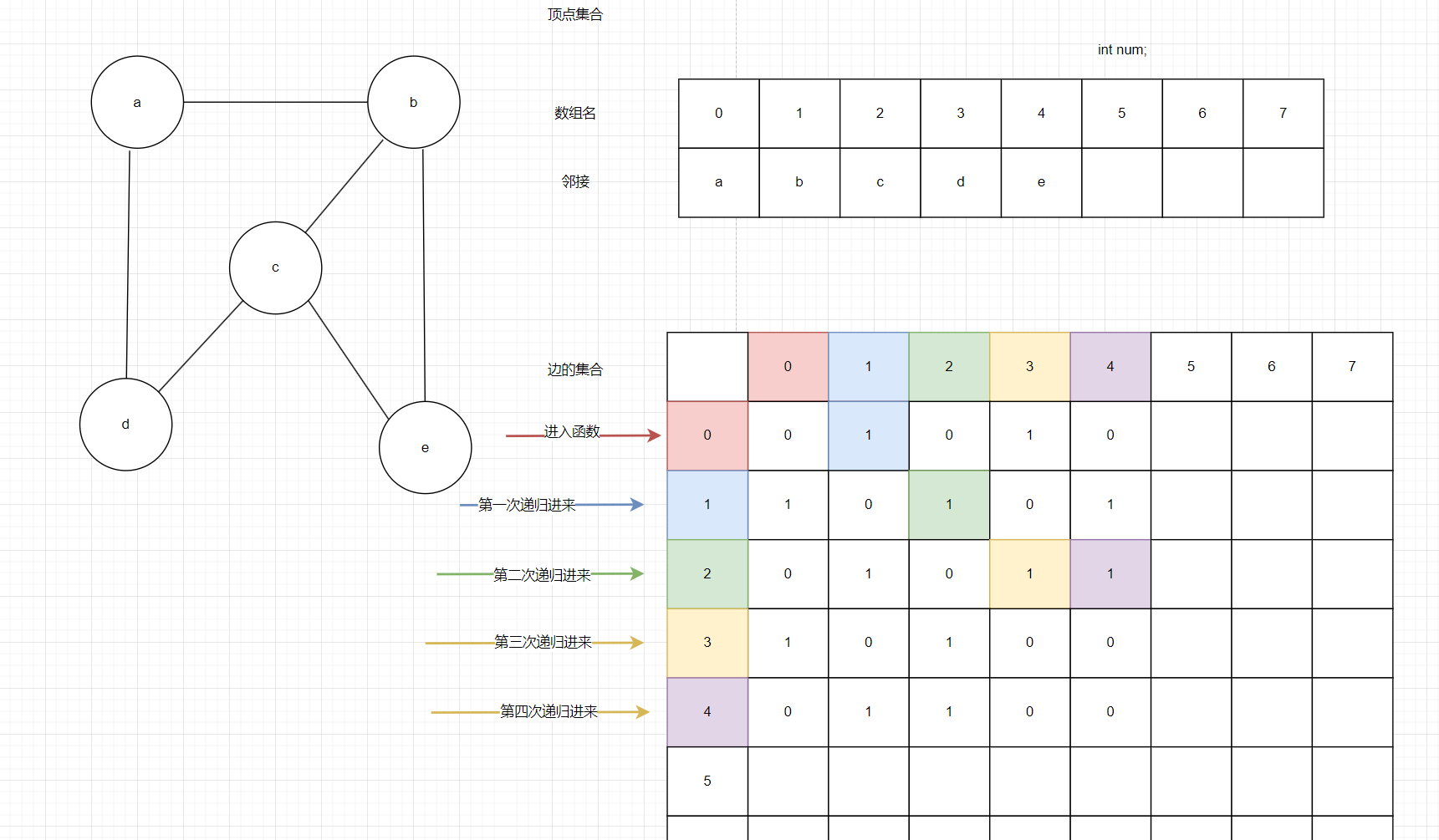
圖2

廣度優先遍歷：void BFS_MGraph(MatrixGraph *graph,int v);

void initVisited() {memset(MGraphVisited, 0, sizeof(MGraphVisited));
}void BFS_MGraph(MatrixGraph *graph,int v) {int front=0;int rear=0;MatrixVertex *queue[MaxNodeNum];queue[rear]=&graph->vex[v];// 在入隊的同時就標記為已訪問MGraphVisited[v] = 1;rear=(rear+1)%MaxNodeNum;while (front!=rear) {//出隊MatrixVertex *node=queue[front];int nodeNum=node->no;visitMGraphNode(node);front=(front+1)%MaxNodeNum;//入隊for (int i = 0; i < graph->nodeNum; ++i) {if (isEdge(graph->edges[nodeNum][i])&&MGraphVisited[i]==0) {queue[rear]=&graph->vex[i];MGraphVisited[i] = 1;  // 在入隊的同時就標記為已訪問rear=(rear+1)%MaxNodeNum;}}}
}

注意在上面已經給static int MGraphVisited[MaxNodeNum];賦值了所以在開始執行BFS之前，需要初始化MGraphVisited數組。因為MGraphVisited數組中的元素被標記為已訪問（即值為1）

我們在void BFS_MGraph(MatrixGraph *graph,int v) 里面創建一個臨時隊列，初始化這個隊列時就把傳入的v入隊，并在入隊的同時就標記為已訪問，當隊列不為空時，進行出隊入隊的操作，出隊時創建一個臨時頂點變量node，讓它拿到node的no（因為我們在for循環里需要拿到出隊的元素不斷判斷與其他頂點是否有邊，若有邊就入隊）并訪問它，在for循環里用拿到的nodeNum遍歷graph->vex[nodeNum]和其他頂點是否有邊，其他沒有被訪問的頂點，如果找到滿足條件的頂點，入隊，并在入隊的同時就標記為已訪問。

如圖3，我們假設傳入的時0即a這個頂點，將a入隊，再出隊，出隊的時候直接把5個頂點全部遍歷完，發現1即b頂點和3即d頂點有邊且未被訪問，直接把b和d頂點入隊

把先進來的b出隊，出隊的時候直接把5個頂點全部遍歷完，發現0即a頂點，2即c頂點和4即e頂點有邊但是a頂點已被訪問剩下兩個沒有，直接把c和e頂點入隊

把d出隊，發現1即b頂點和2即c頂點有邊但已被訪問直接開始出隊

重復上述過程直到隊列為空，最終廣搜的順序：a->b->d->c->e。

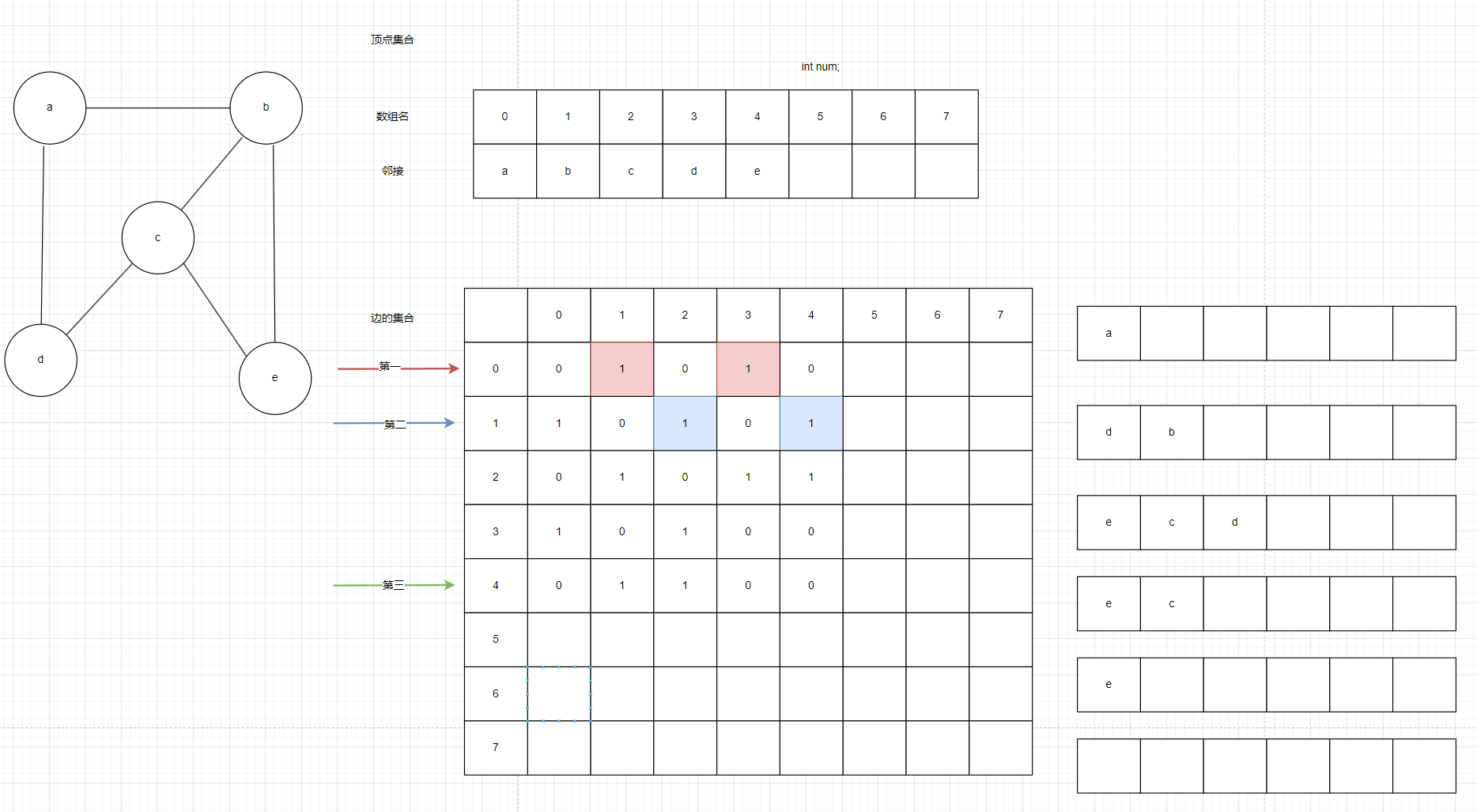
圖3