引言

????????斐波那契堆（Fibonacci Heap）是一種高效的可合并堆數據結構，由 Michael L. Fredman 和 Robert E. Tarjan 于 1984 年提出。它在許多優先隊列操作中提供了極佳的 amortized（攤還）時間復雜度，尤其適用于需要頻繁進行合并操作的場景。

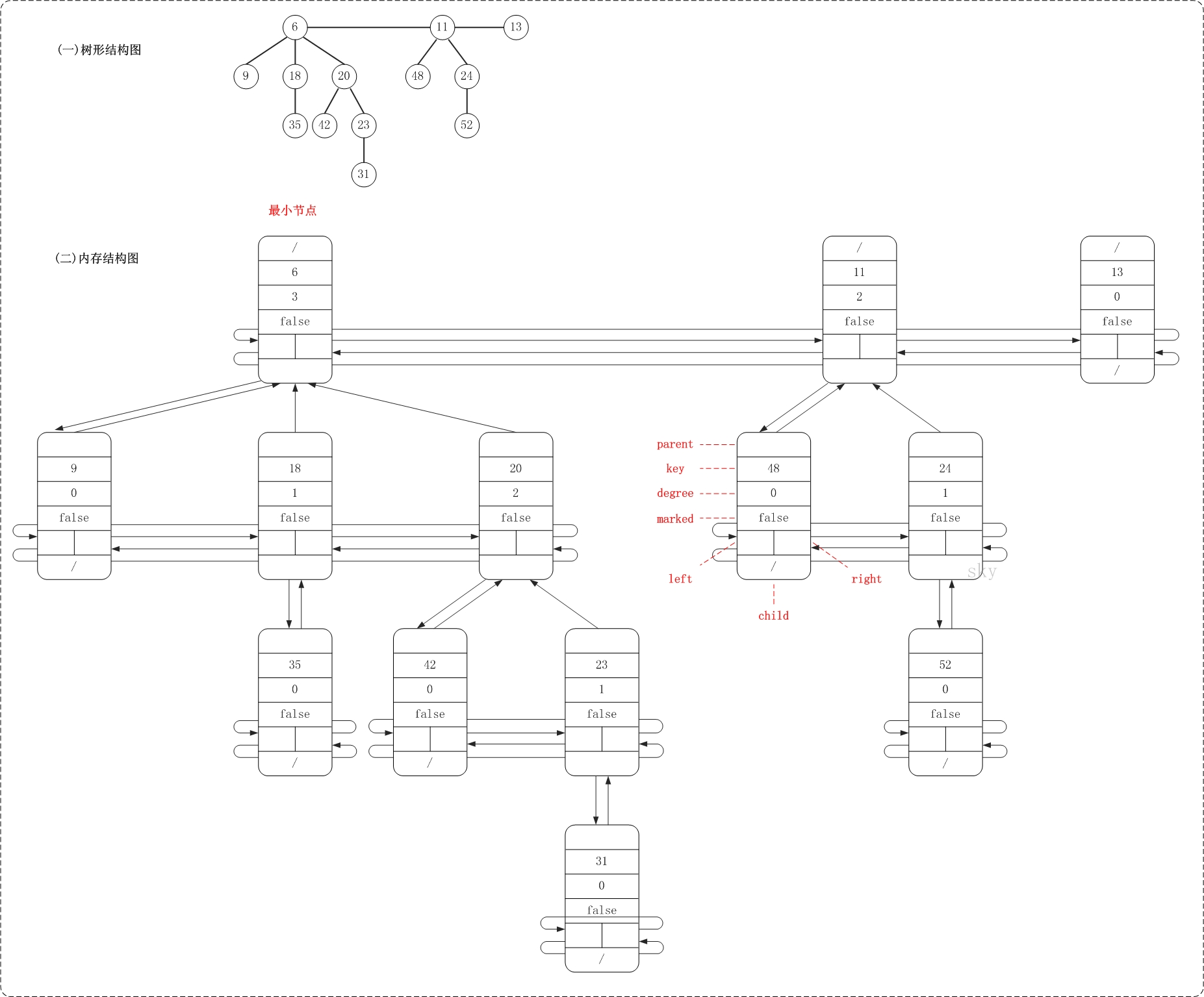
19.1 斐波那契堆結構

19.1.1 基本結構

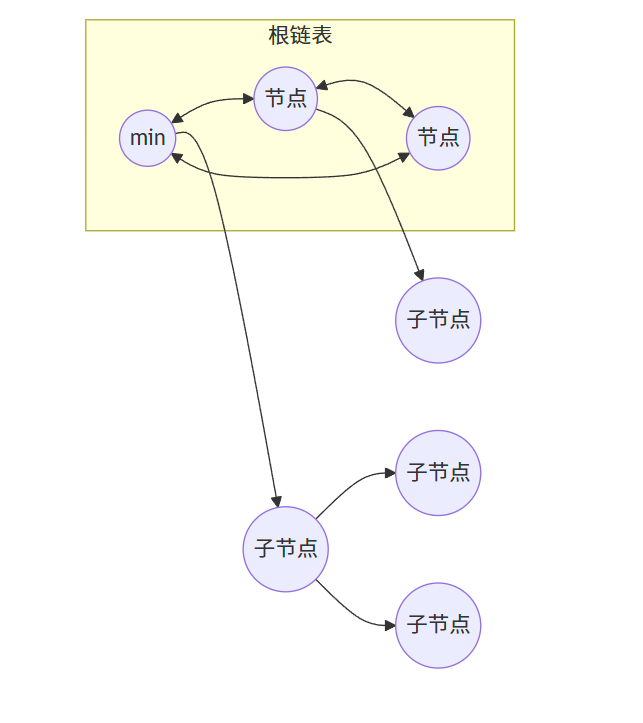
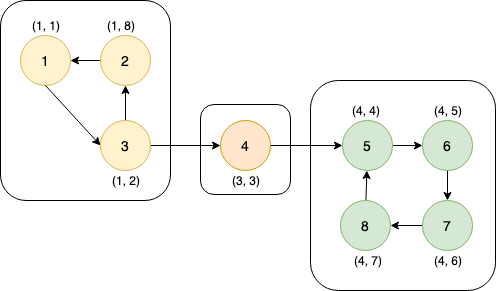
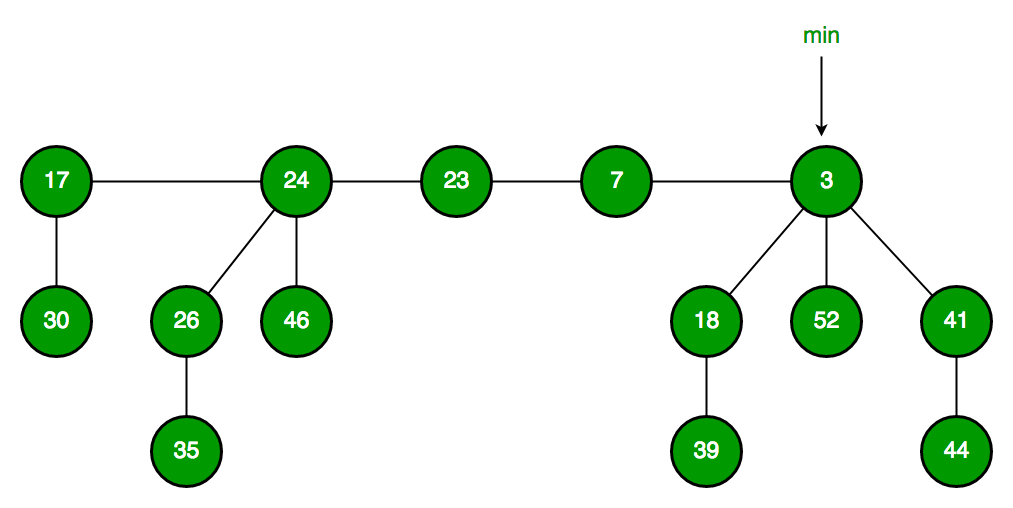
斐波那契堆由一組滿足最小堆性質的樹組成，這些樹都是無序的多叉樹。它包含以下關鍵組件：

1. 一個指向具有最小關鍵字的節點的指針（min pointer）
2. 所有樹的根節點通過雙向循環鏈表連接
3. 每個節點包含：
   • 關鍵字值
   • 父節點指針
   • 子節點指針
   • 左、右兄弟節點指針
   • 度數（子節點數量）
   • 一個標記（用于刪除操作）

19.1.2 節點結構定義

下面是斐波那契堆節點的 C++ 結構定義：

#ifndef FIBONACCI_HEAP_H
#define FIBONACCI_HEAP_H#include <iostream>
#include <vector>
#include <stdexcept>// 斐波那契堆節點結構
template <typename T>
struct FibonacciNode {T key;                  // 節點存儲的值int degree;             // 節點的度數（子節點數量）bool mark;              // 標記，用于刪除操作FibonacciNode* parent;  // 父節點指針FibonacciNode* child;   // 子節點指針FibonacciNode* left;    // 左兄弟節點指針FibonacciNode* right;   // 右兄弟節點指針// 構造函數FibonacciNode(const T& k) : key(k), degree(0), mark(false),parent(nullptr), child(nullptr),left(this), right(this) {}
};// 斐波那契堆類
template <typename T>
class FibonacciHeap {
private:FibonacciNode<T>* minNode;  // 指向最小節點的指針int nodeCount;              // 堆中節點的總數// 將節點y從其所在的雙向鏈表中移除void removeNode(FibonacciNode<T>* y);// 將節點y插入到以節點x為頭的雙向鏈表中void addNode(FibonacciNode<T>* x, FibonacciNode<T>* y);// 將節點y設為節點x的子節點void link(FibonacciNode<T>* y, FibonacciNode<T>* x);// 合并相同度數的樹void consolidate();// 切斷節點y與其父節點x之間的連接void cut(FibonacciNode<T>* y, FibonacciNode<T>* x);// 級聯切斷操作void cascadingCut(FibonacciNode<T>* y);// 銷毀堆的輔助函數void destroyHeap(FibonacciNode<T>* node);public:// 構造函數FibonacciHeap() : minNode(nullptr), nodeCount(0) {}// 析構函數~FibonacciHeap();// 插入元素FibonacciNode<T>* insert(const T& key);// 查找最小元素const T& findMin() const;// 抽取最小元素T extractMin();// 合并兩個斐波那契堆void merge(FibonacciHeap<T>& other);// 減小關鍵字值void decreaseKey(FibonacciNode<T>* x, const T& k);// 刪除節點void deleteNode(FibonacciNode<T>* x);// 檢查堆是否為空bool isEmpty() const { return nodeCount == 0; }// 獲取堆中節點數量int size() const { return nodeCount; }
};#endif // FIBONACCI_HEAP_H

19.2 可合并堆操作

????????斐波那契堆支持可合并堆的所有操作，并且大部分操作都能在常數攤還時間內完成。

19.2.1 插入操作

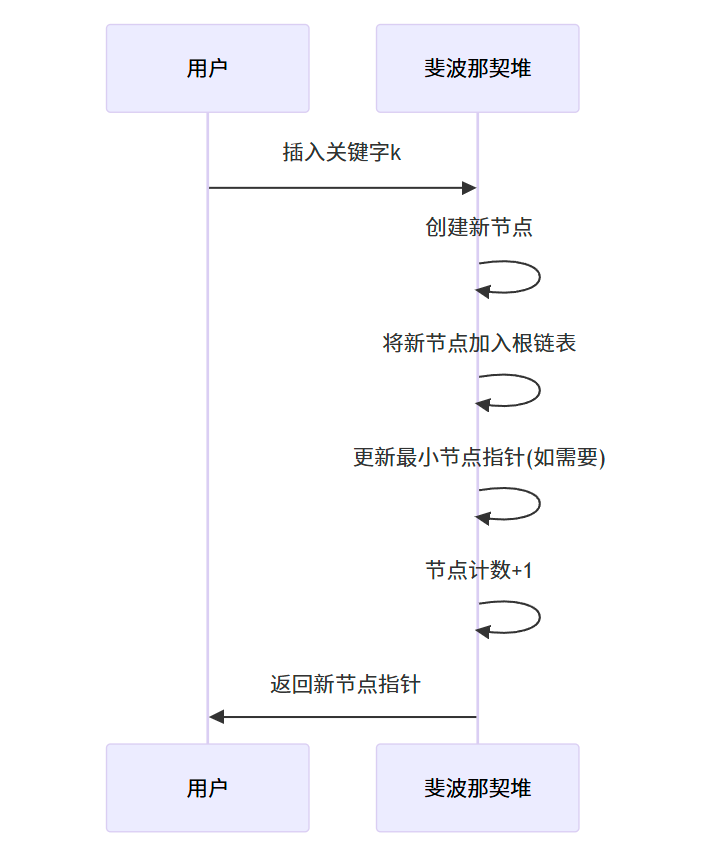
????????插入操作非常簡單，只需創建一個新節點，將其添加到根鏈表中，并更新最小節點指針（如果需要）。

步驟：

1. 創建一個包含關鍵字的新節點
2. 將新節點加入根鏈表
3. 如果新節點的關鍵字小于當前最小節點的關鍵字，更新最小節點指針
4. 節點計數加 1

19.2.2 查找最小元素

????????由于斐波那契堆維護了一個指向最小元素的指針，因此查找最小元素可以在 O (1) 時間內完成。

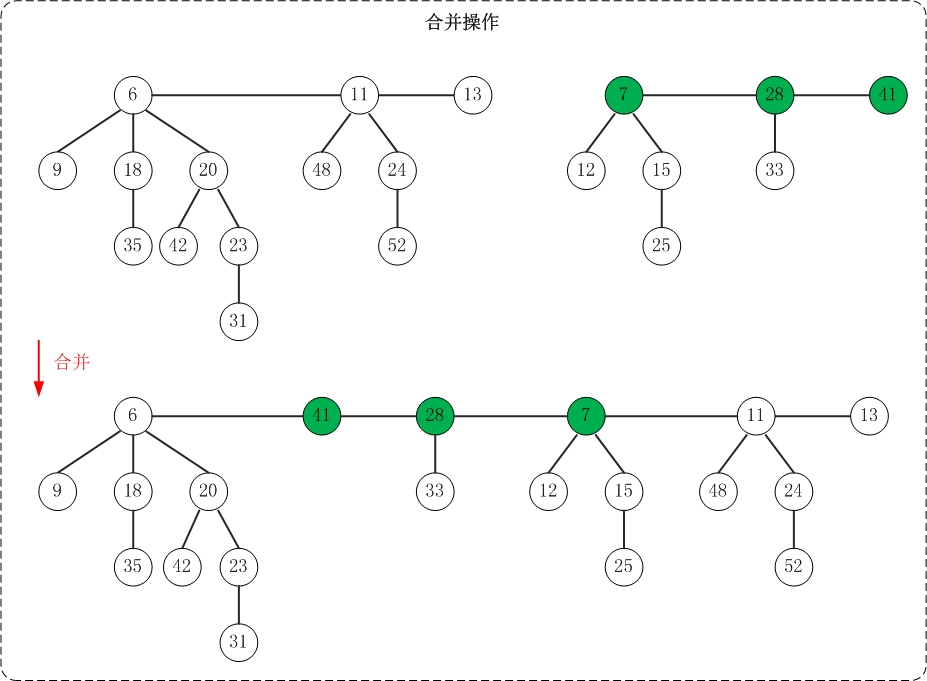
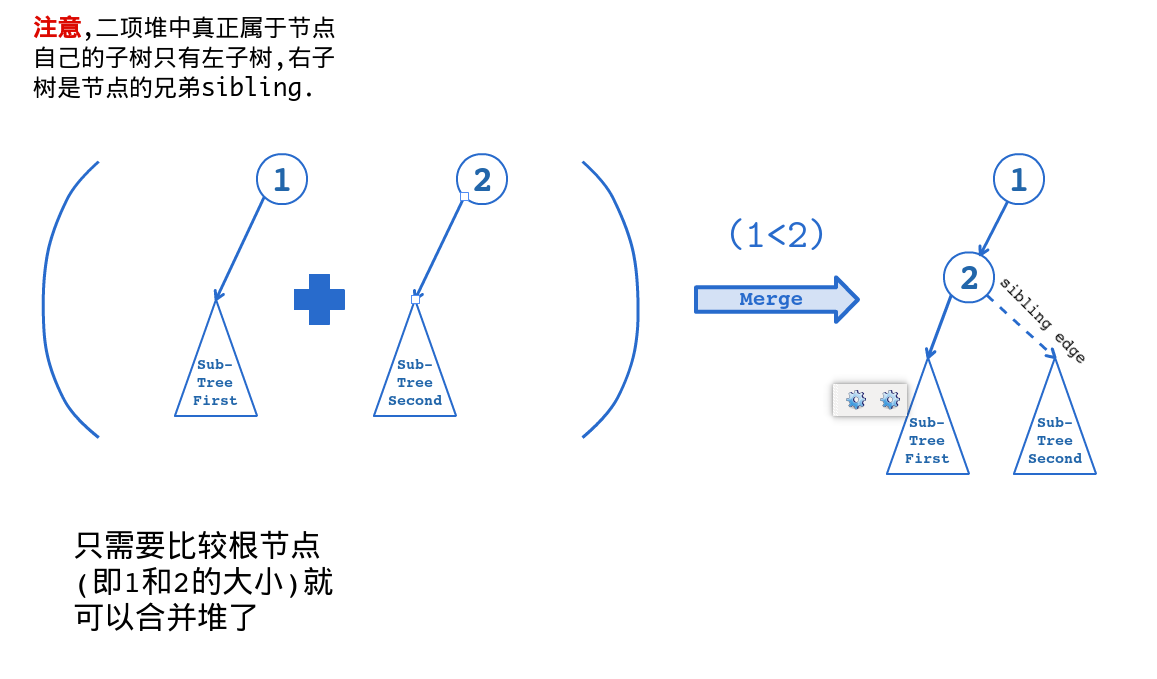
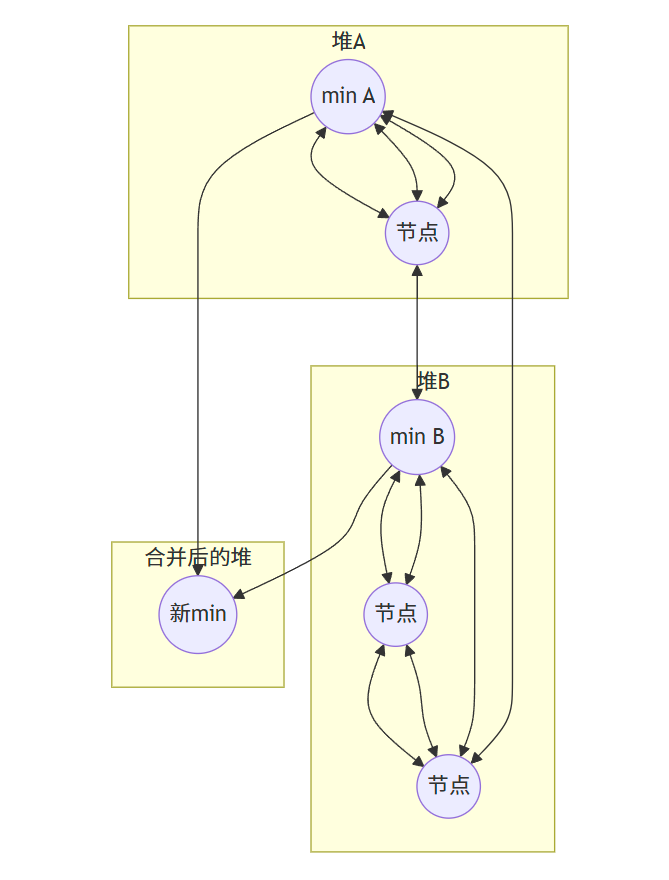
19.2.3 合并操作

????????合并兩個斐波那契堆只需將它們的根鏈表合并成一個雙向鏈表，并更新最小節點指針。

步驟：

1. 合并兩個堆的根鏈表
2. 更新最小節點指針，指向兩個堆中較小的那個最小節點
3. 更新節點計數

19.2.4 抽取最小元素

????????抽取最小元素是斐波那契堆中最復雜的操作之一，需要進行 "合并"（consolidate）過程來維持斐波那契堆的性質。

步驟：

1. 記錄最小節點的值
2. 將最小節點的所有子節點添加到根鏈表
3. 從根鏈表中移除最小節點
4. 執行 consolidate 操作，合并度數相同的樹
5. 更新最小節點指針
6. 節點計數減 1
7. 返回記錄的最小節點值

下面是上述操作的 C++ 實現：

#include "fibonacci_heap.h"// 將節點y從其所在的雙向鏈表中移除
template <typename T>
void FibonacciHeap<T>::removeNode(FibonacciNode<T>* y) {y->left->right = y->right;y->right->left = y->left;
}// 將節點y插入到以節點x為頭的雙向鏈表中
template <typename T>
void FibonacciHeap<T>::addNode(FibonacciNode<T>* x, FibonacciNode<T>* y) {y->left = x->left;y->right = x;x->left->right = y;x->left = y;
}// 將節點y設為節點x的子節點
template <typename T>
void FibonacciHeap<T>::link(FibonacciNode<T>* y, FibonacciNode<T>* x) {// 從根鏈表中移除yremoveNode(y);y->parent = x;// 將y添加為x的子節點if (x->child == nullptr) {x->child = y;y->left = y->right = y;} else {addNode(x->child, y);}x->degree++;  // 增加x的度數y->mark = false;  // 重置y的標記
}// 合并相同度數的樹
template <typename T>
void FibonacciHeap<T>::consolidate() {// 計算最大可能度數int maxDegree = 0;FibonacciNode<T>* current = minNode;if (current != nullptr) {do {if (current->degree > maxDegree) {maxDegree = current->degree;}current = current->right;} while (current != minNode);}// 創建度數表std::vector<FibonacciNode<T>*> degreeTable(maxDegree + 1, nullptr);// 遍歷根鏈表中的所有節點while (minNode != nullptr) {FibonacciNode<T>* x = minNode;int d = x->degree;// 移除當前節點，以便后續處理removeNode(x);x->left = x->right = x;  // 暫時形成一個單節點鏈表// 合并度數相同的樹while (degreeTable[d] != nullptr) {FibonacciNode<T>* y = degreeTable[d];// 確保x是關鍵字較小的節點if (x->key > y->key) {std::swap(x, y);}// 將y鏈接到xlink(y, x);degreeTable[d] = nullptr;d++;}degreeTable[d] = x;}// 重置最小節點指針minNode = nullptr;// 重建根鏈表并找到新的最小節點for (int i = 0; i <= maxDegree; i++) {if (degreeTable[i] != nullptr) {if (minNode == nullptr) {minNode = degreeTable[i];minNode->left = minNode->right = minNode;} else {addNode(minNode, degreeTable[i]);if (degreeTable[i]->key < minNode->key) {minNode = degreeTable[i];}}}}
}// 插入元素
template <typename T>
FibonacciNode<T>* FibonacciHeap<T>::insert(const T& key) {FibonacciNode<T>* newNode = new FibonacciNode<T>(key);if (minNode == nullptr) {// 堆為空，新節點成為根節點minNode = newNode;} else {// 將新節點添加到根鏈表addNode(minNode, newNode);// 更新最小節點if (newNode->key < minNode->key) {minNode = newNode;}}nodeCount++;return newNode;
}// 查找最小元素
template <typename T>
const T& FibonacciHeap<T>::findMin() const {if (minNode == nullptr) {throw std::runtime_error("Heap is empty");}return minNode->key;
}// 抽取最小元素
template <typename T>
T FibonacciHeap<T>::extractMin() {if (minNode == nullptr) {throw std::runtime_error("Heap is empty");}FibonacciNode<T>* z = minNode;T minKey = z->key;// 將z的所有子節點添加到根鏈表if (z->child != nullptr) {FibonacciNode<T>* child = z->child;do {FibonacciNode<T>* nextChild = child->right;// 移除子節點的父指針child->parent = nullptr;// 將子節點添加到根鏈表addNode(minNode, child);child = nextChild;} while (child != z->child);}// 從根鏈表中移除zremoveNode(z);// 如果z是堆中唯一的節點if (z == z->right) {minNode = nullptr;} else {minNode = z->right;// 合并相同度數的樹consolidate();}nodeCount--;delete z;return minKey;
}// 合并兩個斐波那契堆
template <typename T>
void FibonacciHeap<T>::merge(FibonacciHeap<T>& other) {if (other.minNode == nullptr) {return;  // 另一個堆為空，無需合并}if (minNode == nullptr) {// 當前堆為空，直接使用另一個堆minNode = other.minNode;nodeCount = other.nodeCount;} else {// 合并兩個根鏈表FibonacciNode<T>* thisLeft = minNode->left;FibonacciNode<T>* otherLeft = other.minNode->left;minNode->left = otherLeft;otherLeft->right = minNode;thisLeft->right = other.minNode;other.minNode->left = thisLeft;// 更新最小節點if (other.minNode->key < minNode->key) {minNode = other.minNode;}nodeCount += other.nodeCount;}// 清空另一個堆other.minNode = nullptr;other.nodeCount = 0;
}// 析構函數
template <typename T>
FibonacciHeap<T>::~FibonacciHeap() {if (minNode != nullptr) {destroyHeap(minNode);}
}// 銷毀堆的輔助函數
template <typename T>
void FibonacciHeap<T>::destroyHeap(FibonacciNode<T>* node) {if (node == nullptr) return;FibonacciNode<T>* current = node;bool isFirst = true;// 遍歷當前鏈表中的所有節點while (isFirst || current != node) {isFirst = false;FibonacciNode<T>* next = current->right;// 遞歸銷毀子節點destroyHeap(current->child);delete current;current = next;}
}

19.2.5 綜合案例：優先級隊列

????????斐波那契堆非常適合實現優先級隊列，特別是需要頻繁合并操作的場景。以下是一個使用斐波那契堆實現優先級隊列的示例：

#include "fibonacci_heap.h"
#include <iostream>
#include <string>// 任務結構體，表示一個優先級隊列中的任務
struct Task {int priority;  // 優先級，值越小優先級越高std::string description;  // 任務描述// 重載小于運算符，用于斐波那契堆的比較bool operator<(const Task& other) const {return priority < other.priority;}// 重載大于運算符bool operator>(const Task& other) const {return priority > other.priority;}
};// 輸出任務信息
std::ostream& operator<<(std::ostream& os, const Task& task) {os << "任務: " << task.description << ", 優先級: " << task.priority;return os;
}int main() {try {// 創建兩個斐波那契堆作為優先級隊列FibonacciHeap<Task> pq1, pq2;// 向第一個優先級隊列添加任務pq1.insert({3, "完成算法作業"});pq1.insert({1, "緊急會議"});pq1.insert({5, "回復郵件"});// 向第二個優先級隊列添加任務pq2.insert({2, "準備演示文稿"});pq2.insert({4, "整理文檔"});std::cout << "合并前的優先級隊列1大小: " << pq1.size() << std::endl;std::cout << "合并前的優先級隊列2大小: " << pq2.size() << std::endl;// 合并兩個優先級隊列pq1.merge(pq2);std::cout << "合并后的優先級隊列大小: " << pq1.size() << std::endl;std::cout << "合并后隊列為空? " << (pq1.isEmpty() ? "是" : "否") << std::endl;std::cout << "被合并的隊列為空? " << (pq2.isEmpty() ? "是" : "否") << std::endl;// 按優先級處理任務std::cout << "\n按優先級處理任務:" << std::endl;while (!pq1.isEmpty()) {Task highestPriority = pq1.extractMin();std::cout << "處理: " << highestPriority << std::endl;}std::cout << "\n所有任務處理完畢，隊列為空? " << (pq1.isEmpty() ? "是" : "否") << std::endl;} catch (const std::exception& e) {std::cerr << "發生錯誤: " << e.what() << std::endl;return 1;}return 0;
}

19.3 關鍵字減值和刪除一個結點

19.3.1 關鍵字減值

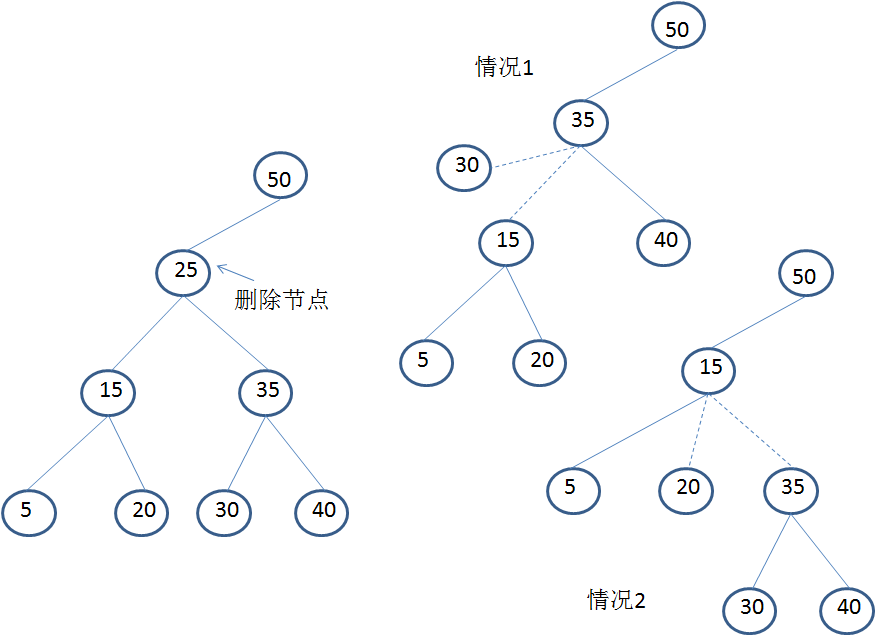
????????關鍵字減值操作用于減小某個節點的關鍵字值，并可能需要調整堆的結構以維持最小堆性質。

步驟：

1. 如果新關鍵字大于當前關鍵字，拋出異常
2. 更新節點的關鍵字值
3. 如果節點的父節點關鍵字大于新關鍵字，切斷該節點與父節點的連接
4. 執行級聯切斷操作，確保斐波那契堆的性質

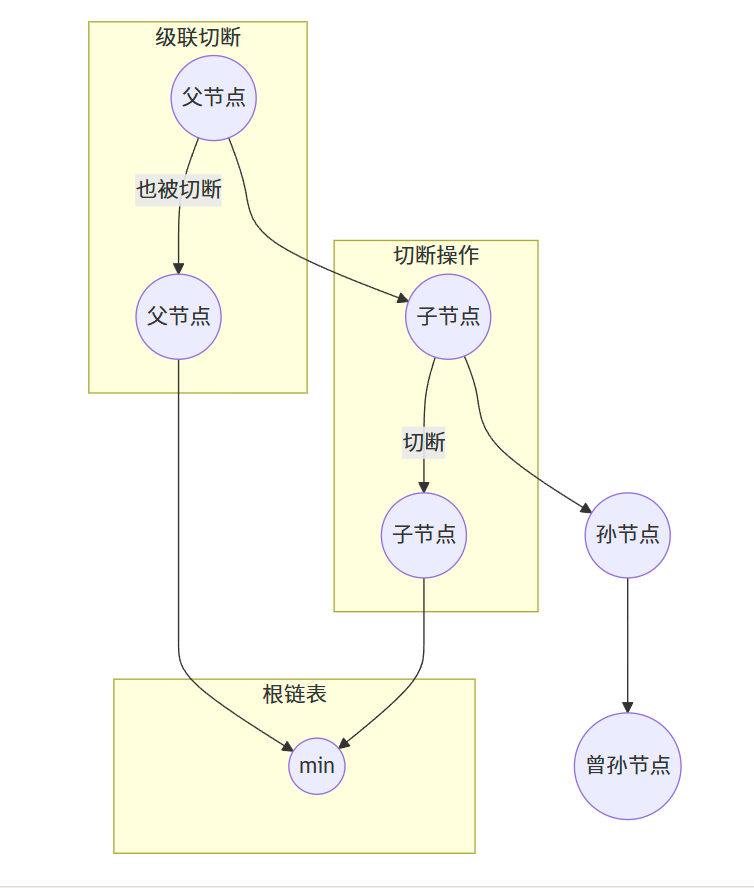
19.3.2 切斷和級聯切斷

• 切斷（cut）：將一個節點從其父節點的子鏈表中移除，并將其添加到根鏈表中
• 級聯切斷（cascading cut）：如果一個節點的子節點被切斷，檢查該節點是否也需要被切斷，遞歸執行直到遇到一個未被標記的節點或根節點

19.3.3 刪除一個節點

刪除一個節點可以通過以下步驟實現：

1. 將該節點的關鍵字減值為負無窮大（或最小可能值）
2. 執行抽取最小元素操作，將該節點從堆中移除

下面是關鍵字減值和刪除操作的 C++ 實現：

#include "fibonacci_heap.h"// 切斷節點y與其父節點x之間的連接
template <typename T>
void FibonacciHeap<T>::cut(FibonacciNode<T>* y, FibonacciNode<T>* x) {// 從x的子鏈表中移除yremoveNode(y);x->degree--;// 如果x的子節點指針指向y，更新子節點指針if (x->child == y) {x->child = y->right;if (x->child == y) {  // 如果y是x唯一的子節點x->child = nullptr;}}// 將y添加到根鏈表addNode(minNode, y);y->parent = nullptr;y->mark = false;  // 重置標記
}// 級聯切斷操作
template <typename T>
void FibonacciHeap<T>::cascadingCut(FibonacciNode<T>* y) {FibonacciNode<T>* z = y->parent;if (z != nullptr) {if (!y->mark) {// 如果y未被標記，標記它y->mark = true;} else {// 如果y已被標記，切斷y并繼續級聯切斷cut(y, z);cascadingCut(z);}}
}// 減小關鍵字值
template <typename T>
void FibonacciHeap<T>::decreaseKey(FibonacciNode<T>* x, const T& k) {if (k > x->key) {throw std::invalid_argument("New key is larger than current key");}x->key = k;FibonacciNode<T>* y = x->parent;// 如果x的關鍵字小于其父節點的關鍵字，需要調整if (y != nullptr && x->key < y->key) {cut(x, y);cascadingCut(y);}// 更新最小節點if (x->key < minNode->key) {minNode = x;}
}// 刪除節點
template <typename T>
void FibonacciHeap<T>::deleteNode(FibonacciNode<T>* x) {// 將x的關鍵字減小到負無窮大（這里使用一個非常小的值模擬）T minPossible = x->key;// 假設T是數值類型，這里簡單地將其設置為一個極小值decreaseKey(x, minPossible - minPossible - minPossible);// 抽取最小元素（即x）extractMin();
}// 顯式實例化常用類型，避免鏈接錯誤
template class FibonacciHeap<int>;
template class FibonacciHeap<double>;
template class FibonacciHeap<Task>;  // 為前面示例中的Task類型實例化

19.3.4 綜合案例：動態優先級調整

????????在許多實際應用中，我們需要能夠動態調整任務的優先級。以下示例展示了如何使用斐波那契堆的關鍵字減值操作來實現這一功能：

#include "fibonacci_heap.h"
#include <iostream>
#include <string>
#include <vector>// 任務結構體
struct Task {int priority;std::string description;bool operator<(const Task& other) const {return priority < other.priority;}bool operator>(const Task& other) const {return priority > other.priority;}
};// 輸出任務信息
std::ostream& operator<<(std::ostream& os, const Task& task) {os << "[" << task.priority << "] " << task.description;return os;
}int main() {try {FibonacciHeap<Task> taskHeap;std::vector<FibonacciNode<Task>*> taskNodes;// 添加一些初始任務taskNodes.push_back(taskHeap.insert({5, "編寫文檔"}));taskNodes.push_back(taskHeap.insert({3, "測試代碼"}));taskNodes.push_back(taskHeap.insert({7, "修復低優先級bug"}));taskNodes.push_back(taskHeap.insert({2, "準備會議"}));taskNodes.push_back(taskHeap.insert({8, "優化性能"}));std::cout << "初始任務隊列:" << std::endl;FibonacciHeap<Task> tempHeap;tempHeap.merge(taskHeap);  // 創建一個副本用于展示while (!tempHeap.isEmpty()) {std::cout << "  " << tempHeap.extractMin() << std::endl;}// 調整一些任務的優先級std::cout << "\n調整任務優先級:" << std::endl;std::cout << "  將\"修復低優先級bug\"的優先級從7調整為1" << std::endl;taskHeap.decreaseKey(taskNodes[2], {1, "修復緊急bug"});std::cout << "  將\"優化性能\"的優先級從8調整為4" << std::endl;taskHeap.decreaseKey(taskNodes[4], {4, "優化性能"});// 刪除一個任務std::cout << "  刪除任務\"編寫文檔\"" << std::endl;taskHeap.deleteNode(taskNodes[0]);// 按新的優先級處理任務std::cout << "\n按新優先級處理任務:" << std::endl;while (!taskHeap.isEmpty()) {std::cout << "  處理: " << taskHeap.extractMin() << std::endl;}} catch (const std::exception& e) {std::cerr << "發生錯誤: " << e.what() << std::endl;return 1;}return 0;
}

19.4 最大度數的界

????????斐波那契堆的效率很大程度上依賴于其節點的最大度數有一個較小的上界。這個上界與黃金比例有關。

19.4.1 度數界的證明

????????對于一個包含 n 個節點的斐波那契堆，任意節點的度數的上界為 O (log n)。更精確地說，如果 n ≥ 1，則任意節點的度數最多為?log_φ n?，其中 φ 是黃金比例（1+√5)/2 ≈ 1.618。

????????這個界限的證明基于斐波那契數的性質：對于度數為 k 的節點，其包含的后代數量至少為第 k+2 個斐波那契數。

19.4.2 斐波那契數與度數的關系

斐波那契數定義為：

• F? = 0
• F? = 1
• F? = F??? + F??? （對于 k ≥ 2）

度數為 k 的節點至少有 F???個后代（包括自身）。

????????度數為0

????????????????至少F?=1個節點

????????度數為1

????????????????至少F?=2個節點

????????度數為2

????????????????至少F?=3個節點

????????度數為3

????????????????至少F?=5個節點

????????度數為k

????????????????至少F???個節點

19.4.3 實際意義

????????這個度數界限保證了斐波那契堆的 consolidate 操作能在 O (log n) 時間內完成，從而確保了抽取最小元素和刪除操作的攤還時間復雜度為 O (log n)。

思考題

1. 比較斐波那契堆與二叉堆、二項堆在各種操作上的時間復雜度，并分析各自的適用場景。

2. 如何修改斐波那契堆的實現，使其支持最大堆而不是最小堆？

3. 證明：在一個斐波那契堆中，包含 n 個節點的樹的最大度數為 O (log n)。

4. 實現一個基于斐波那契堆的 Dijkstra 算法，用于求解單源最短路徑問題。

5. 分析斐波那契堆在實際應用中的優缺點，為什么在很多編程語言的標準庫中沒有采用斐波那契堆？

本章注記

????????斐波那契堆由 Fredman 和 Tarjan 于 1984 年提出，是數據結構設計中的一個重要里程碑。它展示了攤還分析技術如何用于設計高效的數據結構。

????????盡管斐波那契堆在理論上具有優異的時間復雜度，但在實際應用中，由于其實現的復雜性和較高的常數因子，它并不總是最佳選擇。在許多情況下，二項堆或甚至二叉堆可能表現得更好。

????????斐波那契堆的思想啟發了其他高效數據結構的設計，如配對堆（Pairing Heap），它在實踐中往往比斐波那契堆表現更好，同時保持了簡單性。

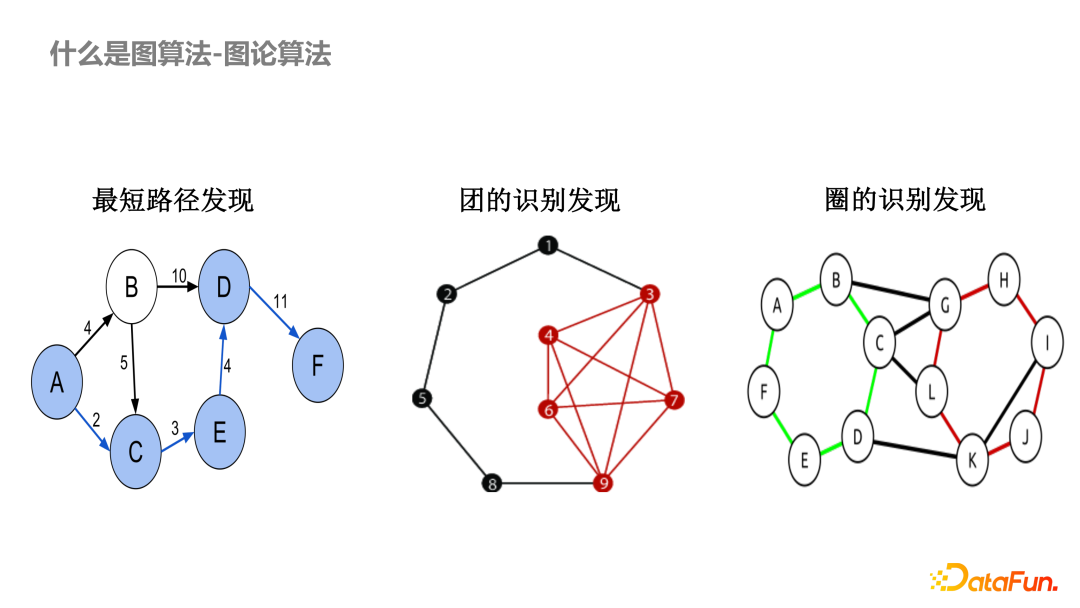
????????斐波那契堆在算法設計中有著重要應用，特別是在圖算法中，如用于實現高效的最小生成樹算法和最短路徑算法。

完整代碼使用說明

為了使用本文實現的斐波那契堆，您需要：

1. 將節點結構和類定義保存為 "fibonacci_heap.h"
2. 將基本操作實現保存為 "fibonacci_heap.cpp"
3. 將關鍵字減值和刪除操作實現保存為 "fibonacci_heap_decrease_delete.cpp"
4. 根據需要使用示例代碼，如優先級隊列或動態優先級調整示例

編譯時，確保將所有源文件一起編譯。例如，使用 g++：

g++ -std=c++11 fibonacci_heap.cpp fibonacci_heap_decrease_delete.cpp priority_queue_example.cpp -o fib_heap_example

總結

????????斐波那契堆是一種理論上非常高效的可合并堆數據結構，它的設計展示了如何通過巧妙的數據結構組織和攤還分析來獲得優異的時間復雜度。雖然實現復雜，但它為許多算法問題提供了最優解，特別是那些需要頻繁合并操作的場景。

????????通過本文的講解和實現示例，希望讀者能夠深入理解斐波那契堆的工作原理，并能在實際應用中靈活運用這一強大的數據結構。