以下是基于筆記更詳細的知識梳理，從概念到細節逐層拆解，幫你吃透數據結構核心要點：

數據結構部分的重點內容：

一、數據結構基礎框架

（一）邏輯結構（關注元素間“邏輯關系”）

筆記里提到“集合、線性、樹形、圖形結構”，具體含義：

• 集合結構：元素間僅“同屬一個集合”的關系，無明確關聯規則（如存一批用戶 ID，相互獨立 ）。

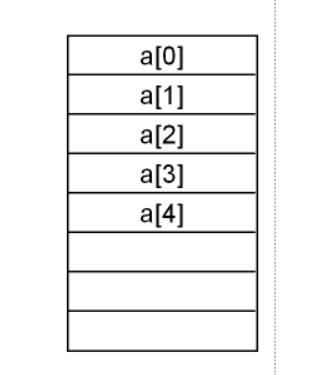
• 線性結構：元素像排隊，一對一順序關聯（如數組、鏈表，每個元素（除首尾）有唯一前驅和后繼 ）。

• 

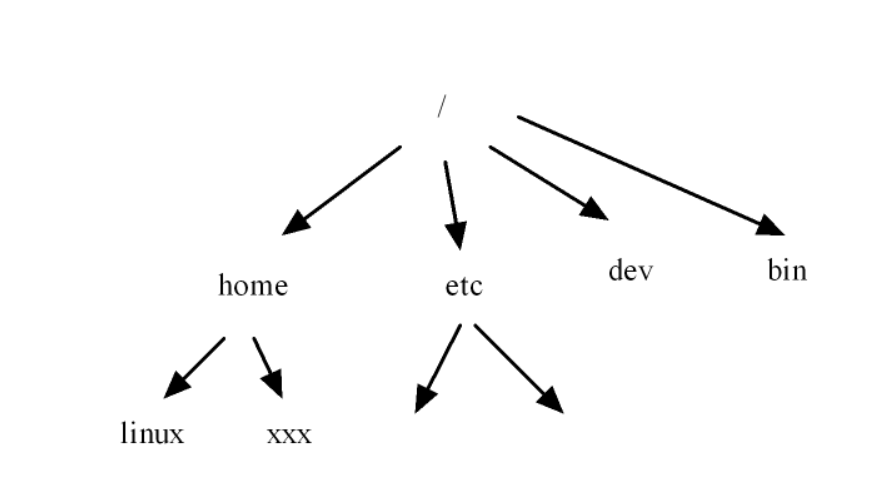
• 樹形結構：元素是“一對多”層級關系（如公司組織架構，總經理→部門經理→員工 ），典型如二叉樹（每個節點最多倆子節點 ）。

• 

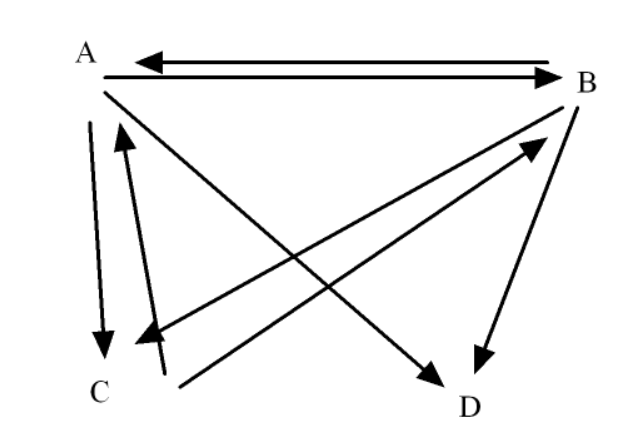
• 圖形結構：元素“多對多”關聯（如社交網絡好友關系，A 可連 B、C，B 也能連 C、D ），強調復雜網狀連接。
  

（二）物理結構（關注“內存怎么存” ）

筆記里的順序、鏈式、索引、散列，是數據在內存的存儲方式，直接影響增刪查改效率：

• 順序結構（如數組）

  • 存儲特點：占一整塊連續內存，像火車車廂連成片。比如 int arr[5]，5 個 int 依次存在內存，地址連續。
  • 訪問效率：因內存連續，用下標訪問（如 arr[2] ），CPU 直接算偏移量，時間復雜度 $O(1)$（秒查 ）。
  • 增刪痛點：插入/刪除元素，后續元素得“搬家”。比如數組 [1,2,3,4] 要在第 2 位插 5，就得把 2、3、4 后移，數據量大時超耗時，復雜度 $O(n)$ 。
  • 內存碎片隱患：若提前分配大內存（比如預開 100 長度數組，實際只用 20 ），剩下 80 可能因“不連續”被浪費（內部碎片 ）。

• 鏈式結構（如鏈表）

  • 存儲特點：元素（節點）分散在內存，靠指針“牽線”。每個節點存數據 + 指向下一節點的指針（單向鏈表 ），雙向鏈表還多一個指向前驅的指針。
  • 增刪優勢：插入/刪除只需改指針。比如單向鏈表刪節點 B，只要讓 A 的指針跳過 B 指 C；插入同理，改前后指針就行，復雜度 $O(1)$（定位到位置后秒改 ）。
  • 查找劣勢：因內存不連續，找元素得從頭遍歷。比如找第 10 個節點，必須從表頭開始，一個個指針跳，復雜度 $O(n)$（數據多了超慢 ）。
  • 內存利用靈活：不用預分配連續大內存，元素按需“零散”分配，能減少內部碎片，但動態分配多了可能產生外部碎片（小內存塊難利用 ）。

• 索引結構（筆記里“索引表”相關）

  • 核心邏輯：額外建“索引表”，存數據關鍵字 + 對應存儲位置（地址 ）。比如查字典，索引表像“目錄”，找 “數據結構” 詞條，先查目錄找頁碼，再翻對應頁。
  • 適用場景：數據量大、查詢頻繁時，用索引加速。比如數據庫查用戶，用 “手機號” 做索引，不用遍歷全表，直接定位存儲位置，查得快。
  • 代價：維護索引表占額外內存，且增刪數據時，索引表也得跟著更新，耗性能。

• 散列結構（哈希表）

  • 核心邏輯：用 哈希函數，把數據關鍵字（如用戶 ID ）映射成內存地址。比如哈希函數 f(key)=key%10，key=123 就存在地址 123%10=3 位置。
  • 查詢優勢：理想情況，直接算地址訪問，復雜度 $O(1)$（和數組下標訪問一樣快 ）。
  • 哈希沖突問題：不同關鍵字可能算出相同地址（比如 12 和 22 都 %10=2 ），得用鏈表法、開放尋址法解決，處理沖突會增加復雜度。

二、鏈表（筆記重點，掰開揉碎講）

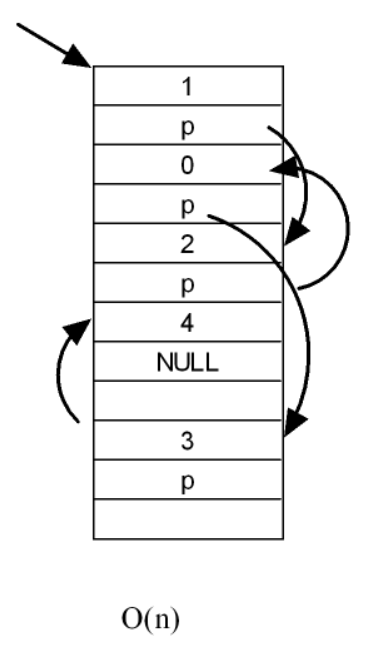
（一）鏈表的“家族成員”

筆記里提到單向、雙向、內核鏈表、循環鏈表，逐個說：

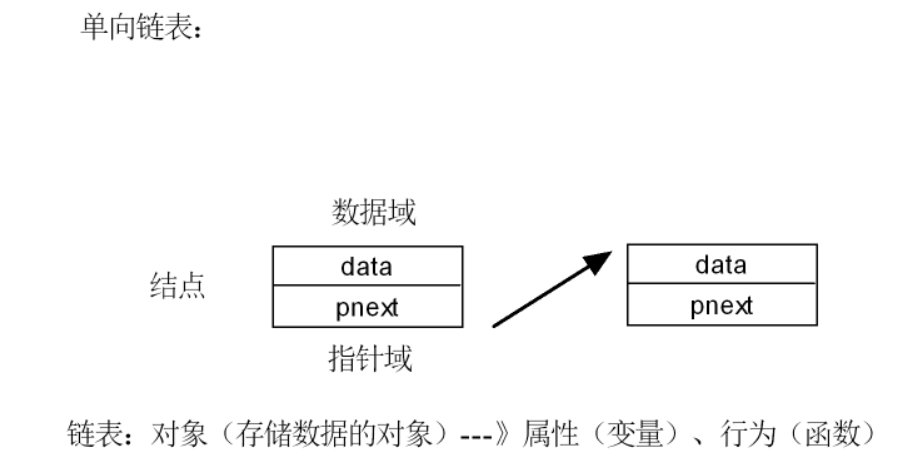
• 單向鏈表

  • 結構：節點 = 數據域（存值，如 int data ） + 指針域（存下一節點地址，如 struct node *pnext ）。表頭是 *phead，表尾節點 pnext=NULL（標志結束 ）。
  • 操作限制：只能從表頭往后遍歷，想找前一個節點？沒指針，得從頭再來，所以反向操作超麻煩（比如刪節點，得先找它前驅，單向鏈表只能遍歷 ）。

• 雙向鏈表

  • 結構升級：節點多一個指針域（struct node *pprev ），指向前一節點。這樣，往前、往后遍歷都能實現。
  • 實用場景：頻繁需要“前后跳轉”的場景。比如瀏覽器歷史記錄，回退（往前找 ）、前進（往后找 ），雙向鏈表更順手。

• 循環鏈表

  • 變種玩法：表尾節點的 pnext 不指向 NULL，而是指向表頭，形成環。比如單向循環鏈表，從任意節點出發，能遍歷全表；雙向循環鏈表同理，前后指針都能繞環。
  • 典型應用：操作系統“時間片輪轉”調度，多個進程用循環鏈表管理，輪流執行，到表尾自動回到表頭。

• 內核鏈表（進階，理解設計思想）

  • 設計巧妙：不把數據直接放節點，而是讓節點“嵌入”數據結構里。比如 Linux 內核鏈表，用 struct list_head 做通用節點，其他結構體（如進程控制塊 task_struct ）包含這個節點，實現“用一套鏈表代碼管理所有數據”，高度解耦、復用性強。

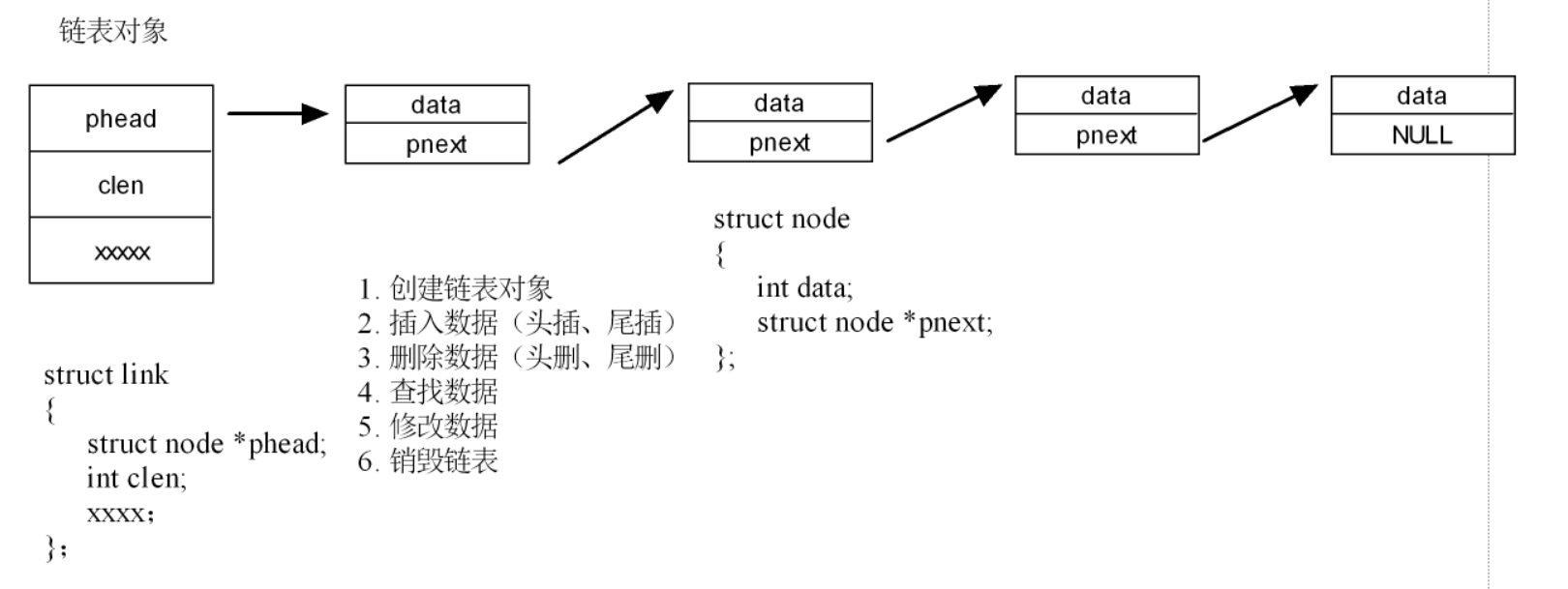
（二）鏈表的“對象封裝”（筆記里 struct link 相關 ）

• 為啥封裝：直接操作節點太零散，封裝成“鏈表對象”，方便管理。
• struct link 里的“小心思”：
  • struct node *phead：表頭指針，找鏈表入口。
  • int clen：存節點個數，想知道鏈表多長，直接讀 clen，不用遍歷統計。
  • 操作函數配套：創建鏈表（init_link() ）、插入節點（insert_node() ）、刪除節點（delete_node() ）、銷毀鏈表（destroy_link() ）等，把鏈表當“對象”用，邏輯更清晰。

三、內存碎片（筆記里“內/外碎片” ）

（一）內部碎片

• 咋產生的：用順序結構（如數組）或某些“規則數據類型”時，預分配的內存沒被完全利用。比如 C 語言 struct 按內存對齊分配，可能多占幾個字節；數組開 100 長度，只用 50，剩下 50 因“屬于數組”不能被其他數據用，成了內部碎片。

（二）外部碎片

• 核心問題：動態分配內存（如鏈表頻繁 malloc ），釋放后，小內存塊“零散分布”，無法合并成大內存塊。比如多次 malloc 小節點，釋放后內存里有很多小空閑塊，新數據要大內存時，這些小塊沒法用，成了外部碎片。

四、數據結構“常用操作基石”

（一）指針

• 關鍵作用：鏈式結構的“命脈”，鏈表靠指針串節點；動態內存分配（malloc ）返回的也是指針，管理堆內存離不開它。

（二）結構體（struct ）

• 定制化容器：把不同類型數據“打包”。比如鏈表節點 struct node，把 int data（數據 ）和 struct node *pnext（指針 ）放一起，讓數據 + 關聯關系“一體化”。

（三）動態內存分配（malloc/free 等 ）

• 靈活雙刃劍：鏈表節點按需 malloc，用多少開多少；但頻繁分配/釋放，容易內存泄漏（忘 free ）、產生外部碎片，得小心管理。

五、總結（知識串聯，更清晰 ）

數據結構的核心是**“用啥結構存數據 + 咋高效操作數據”**：

• 存數據前，選邏輯結構（比如一對一關系用線性結構，多對多用圖形結構 ）。
• 存的時候，選物理結構（數組存連續內存，鏈表存零散內存，索引/散列加速查詢 ）。
• 操作數據時，鏈表靠指針玩“增刪自由”，數組靠下標玩“訪問速度”，各有優劣。

筆記里的鏈表、內存碎片、動態分配，都是圍繞“怎么高效存、改、查數據”展開，理解這些，學隊列、棧、樹、圖時，邏輯會更順（比如隊列基于數組/鏈表實現，本質是線性結構的“特殊規則操作” ）。

課上代碼：

需要做到多練習，自己理解完單向鏈表之后多敲代碼熟練運用：

封裝函數部分：

#include<stdlib.h>
#include<stdio.h>
#include<string.h>
#include"link.h"
LINK_T *creat_link()
{LINK_T *plink=malloc(sizeof(LINK_T));if(plink==NULL){printf("malloc plink error");return NULL;}plink->phead=NULL;plink->clen=0;return plink;
}//頭插入：
int insert_node(LINK_T *plink,node_type data)
{NODE_T *pnode=malloc(sizeof(NODE_T));if(pnode==NULL){printf("malloc pnode error");return -1;}pnode->data=data;pnode->pnext=plink->phead;plink->phead=pnode;plink->clen++;return 0;
}
//遍歷：
void link_for_each(LINK_T *plink)
{NODE_T *p=plink->phead;while(p!=NULL){printf("%d ", p->data );p=p->pnext;}printf("\n");
}
//遍歷查找結點數據：
NODE_T *find_link(LINK_T *plink,node_type data)
{NODE_T *p=plink->phead;while(p!=NULL){if(p->data==data){printf("found!");return p;}p=p->pnext;}return NULL;
}
//修改結點數據：
int change_link(LINK_T *plink,node_type olddata,node_type newdata)
{NODE_T *p=find_link(plink,olddata);if(p==NULL){printf("nofound!");return -1;}p->data=newdata;return 0;
}//頭刪：
void delet_firstNode(LINK_T *plink)
{NODE_T *p=plink->phead;plink->phead=p->pnext;free(p);p=NULL;plink->clen--;
}
//指定數據對應的結點進行刪除：
int delet_specified_node(LINK_T *plink,node_type data)
{NODE_T *p=find_link(plink,data);if(p==NULL){printf("nofound!");return -1;}NODE_T *p_prehand=plink->phead;if(p_prehand==NULL){printf("無結點，無法繼續刪除結點");return -1;}while(p_prehand!=NULL){if(p_prehand->pnext==p){p_prehand->pnext=p->pnext;break;}p_prehand=p_prehand->pnext;}free(p);p=NULL;plink->clen--;return 0;
}
//封裝函數實現單向鏈表的尾插：
NODE_T *findTheLastNode(LINK_T *plink)
{NODE_T *p=plink->phead;if(p==NULL){return NULL;}while(p->pnext!=NULL){p=p->pnext;}return p;
}
int insertOneNodeAtTheEndOfTheLinkedList(LINK_T *plink,node_type data)
{NODE_T *pnode=malloc(sizeof(NODE_T));if(pnode==NULL){printf("malloc error!");return -1;}NODE_T *plastnode=findTheLastNode(plink);if(plastnode==NULL){plink->phead=pnode;plink->clen++;pnode->data=data;pnode->pnext=NULL;}else{plastnode->pnext=pnode;pnode->pnext=NULL;pnode->data=data;plink->clen++;}return 0;
}
//封裝函數實現單向鏈表的尾刪，注意只有一個結點的情況！
int delet_lastnode(LINK_T *plink)
{NODE_T *p=plink->phead;if(p==NULL){printf("無結點可刪除，程序終止！");return -1;}else{if(p->pnext==NULL){free(p);plink->phead=NULL;plink->clen--;return 0;}else{while(p->pnext->pnext!=NULL){p=p->pnext;}free(p->pnext);p->pnext=NULL;plink->clen--;}}return 0;
}
int deletAllNode(LINK_T *plink)
{NODE_T *p=plink->phead;if(p==NULL){printf("無結點可刪除");return -1;}while(plink->phead!=NULL){while(p!=NULL){p=p->pnext;}delet_lastnode(plink);}
}

頭文件部分：

#ifndef _LINK_H_
#define _LINK_H_
typedef int node_type;
typedef struct node
{node_type data;struct node *pnext;
}NODE_T;
typedef struct link
{NODE_T *phead;int clen;
}LINK_T;extern LINK_T *creat_link();
extern int insert_node(LINK_T *plink,node_type data);
extern void link_for_each(LINK_T *plink);
extern NODE_T *find_link(LINK_T *plink,node_type data);
extern int change_link(LINK_T *plink,node_type olddata,node_type newdata);
extern void delet_firstNode(LINK_T *plink);
extern int delet_specified_node(LINK_T *plink,node_type data);
extern NODE_T *findTheLastNode(LINK_T *plink);
extern int insertOneNodeAtTheEndOfTheLinkedList(LINK_T *plink,node_type data);
extern int delet_lastnode(LINK_T *plink);
extern int deletAllNode(LINK_T *plink);
#endif

主函數本部分：

#include<stdio.h>
#include"link.h"
#include<stdlib.h>
int main(void)
{link_t *plink=creat_Link();if(plink==NULL){return -1;}insert_link_head(plink,1);insert_link_head(plink,2);insert_link_head(plink,3);insert_link_head(plink,4);insert_link_head(plink,5);link_for_each(plink);
//	Node_t *pfind=find_link(plink,2);
//	if(pfind==NULL)
//	{
//		printf("nofind");
//	}
//	else
//	{
//		printf("found,value=%d\n",pfind->data);
//	}
//	change_link(plink,2,3);
//	link_for_each(plink);deletFirstNode(plink);return 0;
}