LeetCode 513 - 尋找樹的最后一行的最左側的值，【難度：中等；通過率：73.8%】，這道題是檢驗對兩種核心遍歷策略——廣度優先搜索 (BFS) 和深度優先搜索 (DFS) 理解與運用的絕佳試金石

一、 題目描述

給定一個二叉樹的根節點 root，請找出該二叉樹的 最底層 最左邊 節點的值

假設二叉樹中至少有一個節點

示例:

示例 1:

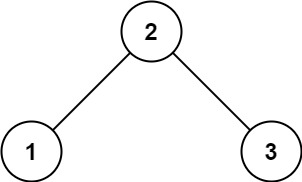
輸入: root = [2,1,3]
輸出: 1

示例 2:

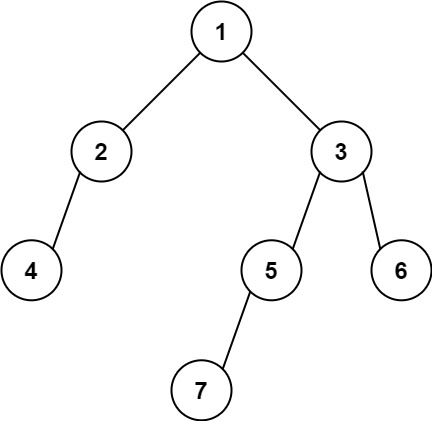
輸入: root = [1,2,3,4,null,5,6,null,null,7]
輸出: 7

---

解法一：層序遍歷 (BFS) - 最直觀的解法

既然問題涉及到“層”和“行”，那么廣度優先搜索 (BFS) 無疑是最自然、最直觀的解題思路。我們只需要逐層遍歷，并想辦法記錄下每一層的第一個節點即可

核心思路

1. 使用隊列進行標準的層序遍歷
2. 在 while 循環中，我們知道每一次循環都將處理新的一層
3. 在開始處理這一層的所有節點之前，隊列的頭部元素 (queue.peek()) 正是這一層的最左側節點
4. 我們用一個變量 resultNode 來不斷更新這個“每層的最左側節點”。當整個 while 循環結束時，resultNode 自然就指向了最后一層的最左側節點

代碼實現

class Solution {public int findBottomLeftValue(TreeNode root) {Queue<TreeNode> queue = new LinkedList<>(); // 也可自行選擇其他高效實現queue.add(root);TreeNode resultNode = null; // 用于記錄最終結果節點while (!queue.isEmpty()) {// 在處理本層節點前，隊列的頭部就是本層的最左側節點// 用 resultNode 把它“暫存”起來resultNode = queue.peek();int levelSize = queue.size(); // 獲取初始當前層的節點數量// 遍歷并處理當前層的所有節點for (int i = 0; i < levelSize; i++) {TreeNode node = queue.poll();// 將下一層的節點（從左到右）加入隊列if (node.left != null) {queue.add(node.left);}if (node.right != null) {queue.add(node.right);}}}// 循環結束后，resultNode 指向的就是最后一層的最左側節點return resultNode.val;}
}

優缺點分析

• 優點：思路與問題描述高度契合，代碼邏輯清晰，易于理解
• 缺點：需要使用隊列，空間復雜度為 O(W)，其中 W 是樹的最大寬度。對于一個茂盛的樹，空間開銷較大

---

解法二：遞歸 (DFS) - 更深度的思考

我們也可以用深度優先搜索（DFS）來解決這個問題。這里的核心思想是：如果我們能記錄下每個節點的深度，那么我們只需要找到擁有最大深度的、并且最靠左的那個節點即可

核心思路

1. 定義兩個全局變量：maxDepth 記錄遍歷過程中遇到的最大深度，resultVal 記錄在最大深度下最左側節點的值
2. 進行一次深度優先搜索（遞歸）。為了確保找到的是“最左側”的節點，我們采用先序遍歷的順序（根-左-右）
3. 在遍歷每個節點時，我們比較當前節點的深度 currentDepth 和已知的最大深度 maxDepth
4. 如果 currentDepth > maxDepth，這意味著我們第一次到達了一個更深的層次。由于我們是先遍歷左子樹，所以當前這個節點一定是這個新深度下的最左側節點。此時，我們更新 maxDepth 和 resultVal
5. 如果 currentDepth <= maxDepth，我們不做任何操作，因為我們已經在這個深度或更深的深度找到了最左側的節點

代碼實現

class Solution {int maxDepth = -1; // 記錄已發現的最大深度int resultVal = 0;   // 記錄最大深度下最左側節點的值public int findBottomLeftValue(TreeNode root) {// 從根節點開始 DFS，初始深度為 0dfs(root, 0);return resultVal;}/*** dfs* @param node  當前節點* @param depth 當前節點的深度*/private void dfs(TreeNode node, int depth) {if (node == null) {return;}// 核心邏輯：判斷是否發現了新的更深層// 因為我們是先序遍歷（先左后右），所以第一次到達一個新深度時，// 當前節點必然是該深度的最左側節點if (depth > maxDepth) {maxDepth = depth; // 更新最大深度resultVal = node.val; // 更新結果值}// 搜索左子樹dfs(node.left, depth + 1);// 搜索右子樹dfs(node.right, depth + 1);}
}

優缺點分析

• 優點：空間復雜度僅為遞歸棧的深度 O(H)，對于窄而深的樹，空間效率優于 BFS
• 缺點：思路相對 BFS 來說不那么直觀，需要正確處理深度和值的更新邏輯

---

四、 總結與對比

	解法一 (層序遍歷 / BFS)	解法二 (遞歸 / DFS)
核心思路	逐層遍歷，不斷用每層的第一個節點覆蓋結果，直到最后一層	深度優先，利用遍歷順序和深度記錄，找到第一個到達最大深度的節點
數據結構	隊列 (Queue)	遞歸棧
時間復雜度	O(N)	O(N)
空間復雜度	O(W) (樹的最大寬度)	O(H) (樹的最大高度)
代碼可讀性	高，與問題描述匹配	中等，需要理解深度更新的邏輯
適用場景	解決所有與“層”相關的問題，通用性強	空間效率可能更高，尤其是在處理細長的樹時